|
Community Structure
In the study of complex networks, a network is said to have community structure if the nodes of the network can be easily grouped into (potentially overlapping) sets of nodes such that each set of nodes is densely connected internally. In the particular case of ''non-overlapping'' community finding, this implies that the network divides naturally into groups of nodes with dense connections internally and sparser connections between groups. But ''overlapping'' communities are also allowed. The more general definition is based on the principle that pairs of nodes are more likely to be connected if they are both members of the same community(ies), and less likely to be connected if they do not share communities. A related but different problem is community search, where the goal is to find a community that a certain vertex belongs to. Properties In the study of networks, such as computer and information networks, social networks and biological networks, a number of different charac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Network
In the context of network theory, a complex network is a graph (network) with non-trivial topological features—features that do not occur in simple networks such as lattices or random graphs but often occur in networks representing real systems. The study of complex networks is a young and active area of scientific research (since 2000) inspired largely by empirical findings of real-world networks such as computer networks, biological networks, technological networks, brain networks, climate networks and social networks. Definition Most social, biological, and technological networks display substantial non-trivial topological features, with patterns of connection between their elements that are neither purely regular nor purely random. Such features include a heavy tail in the degree distribution, a high clustering coefficient, assortativity or disassortativity among vertices, community structure, and hierarchical structure. In the case of directed networks these feat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Similarity Measure
In statistics and related fields, a similarity measure or similarity function or similarity metric is a real-valued function that quantifies the similarity between two objects. Although no single definition of a similarity exists, usually such measures are in some sense the inverse of distance metrics: they take on large values for similar objects and either zero or a negative value for very dissimilar objects. Though, in more broad terms, a similarity function may also satisfy metric axioms. Cosine similarity is a commonly used similarity measure for real-valued vectors, used in (among other fields) information retrieval to score the similarity of documents in the vector space model. In machine learning, common kernel functions such as the RBF kernel can be viewed as similarity functions. Use in clustering In spectral clustering, a similarity, or affinity, measure is used to transform data to overcome difficulties related to lack of convexity in the shape of the data distribut ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
GitHub
GitHub, Inc. () is an Internet hosting service for software development and version control using Git. It provides the distributed version control of Git plus access control, bug tracking, software feature requests, task management, continuous integration, and wikis for every project. Headquartered in California, it has been a subsidiary of Microsoft since 2018. It is commonly used to host open source software development projects. As of June 2022, GitHub reported having over 83 million developers and more than 200 million repositories, including at least 28 million public repositories. It is the largest source code host . History GitHub.com Development of the GitHub.com platform began on October 19, 2007. The site was launched in April 2008 by Tom Preston-Werner, Chris Wanstrath, P. J. Hyett and Scott Chacon after it had been made available for a few months prior as a beta release. GitHub has an annual keynote called GitHub Universe. Organizational ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Extremal Ensemble Learning
Extremal Ensemble Learning (EEL) is a machine learning algorithmic paradigm for graph partitioning. EEL creates an ensemble Ensemble may refer to: Art * Architectural ensemble * Ensemble (album), ''Ensemble'' (album), Kendji Girac 2015 album * Ensemble (band), a project of Olivier Alary * Ensemble cast (drama, comedy) * Ensemble (musical theatre), also known as the ... of partitions and then uses information contained in the ensemble to find new and improved partitions. The ensemble evolves and learns how to form improved partitions through extremal updating procedure. The final solution is found by achieving consensus among its member partitions about what the optimal partition is. Reduced Network Extremal Ensemble Learning (RenEEL) A particular implementation of the EEL paradigm is the Reduced Network Extremal Ensemble Learning (RenEEL) scheme for partitioning a graph. RenEEL uses consensus across many partitions in an ensemble to create a reduced network that can be ef ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Louvain Modularity
The Louvain method for community detection is a method to extract non-overlapping communities from large networks created by Blondel ''et al''. from the University of Louvain (the source of this method's name). The method is a greedy optimization method that appears to run in time O(n \cdot \log n) where n is the number of nodes in the network. Modularity optimization The inspiration for this method of community detection is the optimization of modularity as the algorithm progresses. Modularity is a scale value between −0.5 (non-modular clustering) and 1 (fully modular clustering) that measures the relative density of edges inside communities with respect to edges outside communities. Optimizing this value theoretically results in the best possible grouping of the nodes of a given network. But because going through all possible iterations of the nodes into groups is impractical, heuristic algorithms are used. In the Louvain Method of community detection, first small commu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Modularity (networks)
Modularity is a measure of the structure of networks or graphs which measures the strength of division of a network into modules (also called groups, clusters or communities). Networks with high modularity have dense connections between the nodes within modules but sparse connections between nodes in different modules. Modularity is often used in optimization methods for detecting community structure in networks. However, it has been shown that modularity suffers a resolution limit and, therefore, it is unable to detect small communities. Biological networks, including animal brains, exhibit a high degree of modularity. Motivation Many scientifically important problems can be represented and empirically studied using networks. For example, biological and social patterns, the World Wide Web, metabolic networks, food webs, neural networks and pathological networks are real world problems that can be mathematically represented and topologically studied to reveal some unexpected str ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Betweenness Centrality
In graph theory, betweenness centrality (or "betweeness centrality") is a measure of centrality in a graph based on shortest paths. For every pair of vertices in a connected graph, there exists at least one shortest path between the vertices such that either the number of edges that the path passes through (for unweighted graphs) or the sum of the weights of the edges (for weighted graphs) is minimized. The betweenness centrality for each vertex is the number of these shortest paths that pass through the vertex. Betweenness centrality was devised as a general measure of centrality: it applies to a wide range of problems in network theory, including problems related to social networks, biology, transport and scientific cooperation. Although earlier authors have intuitively described centrality as based on betweenness, gave the first formal definition of betweenness centrality. Betweenness centrality finds wide application in network theory; it represents the degree to which nodes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Girvan–Newman Algorithm
The Girvan–Newman algorithm (named after Michelle Girvan and Mark Newman) is a hierarchical method used to detect communities in complex systems.Girvan M. and Newman M. E. J.Community structure in social and biological networks Proc. Natl. Acad. Sci. USA 99, 7821–7826 (2002) Edge betweenness and community structure The Girvan–Newman algorithm detects communities by progressively removing edges from the original network. The connected components of the remaining network are the communities. Instead of trying to construct a measure that tells us which edges are the most central to communities, the Girvan–Newman algorithm focuses on edges that are most likely "between" communities. Vertex betweenness is an indicator of highly central nodes in networks. For any node i, vertex betweenness is defined as the fraction of shortest paths between pairs of nodes that run through it. It is relevant to models where the network modulates transfer of goods between known start and end n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
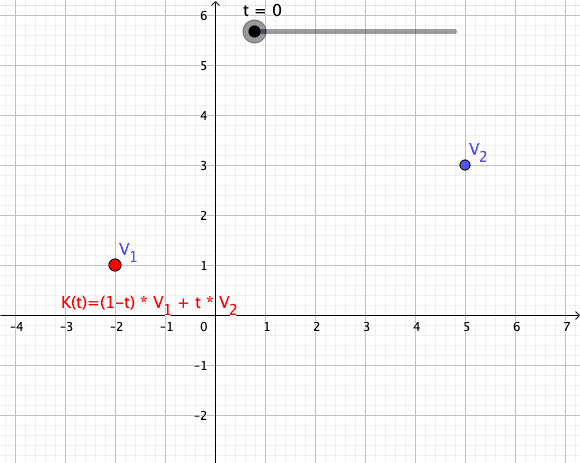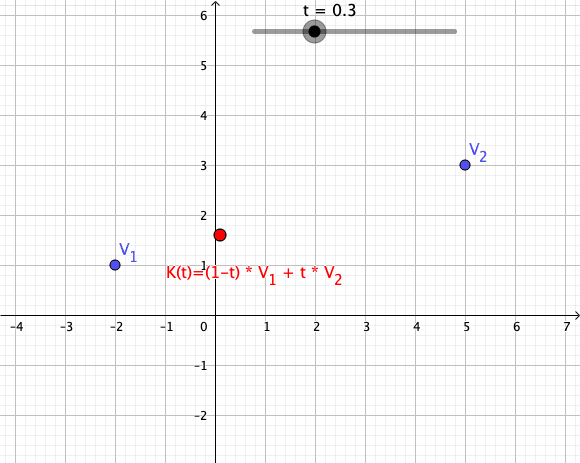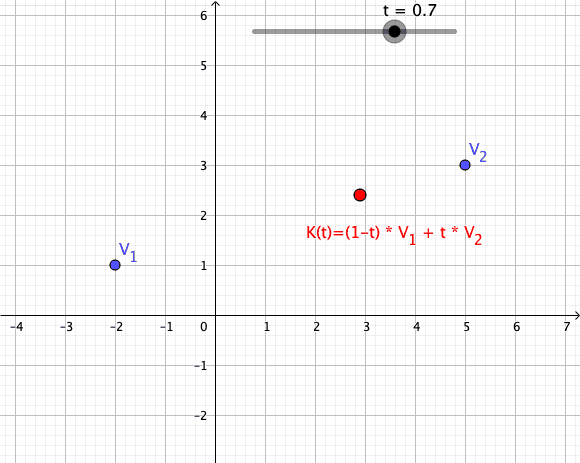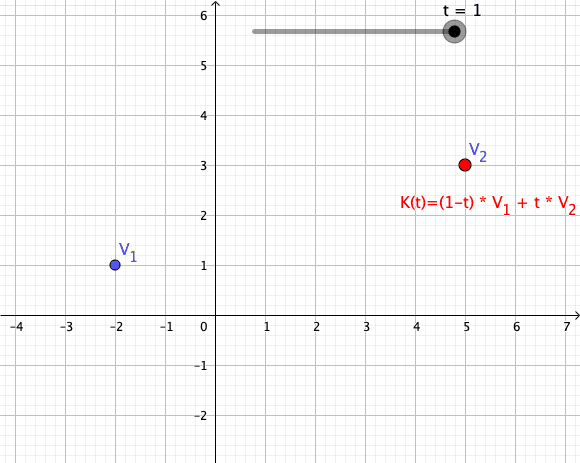
Convex Combination
In convex geometry and vector algebra, a convex combination is a linear combination of points (which can be vectors, scalars, or more generally points in an affine space) where all coefficients are non-negative and sum to 1. In other words, the operation is equivalent to a standard weighted average, but whose weights are expressed as a percent of the total weight, instead of as a fraction of the ''count'' of the weights as in a standard weighted average. More formally, given a finite number of points x_1, x_2, \dots, x_n in a real vector space, a convex combination of these points is a point of the form :\alpha_1x_1+\alpha_2x_2+\cdots+\alpha_nx_n where the real numbers \alpha_i satisfy \alpha_i\ge 0 and \alpha_1+\alpha_2+\cdots+\alpha_n=1. As a particular example, every convex combination of two points lies on the line segment between the points. A set is convex if it contains all convex combinations of its points. The convex hull of a given set of points is identical ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complete Linkage Clustering
Complete-linkage clustering is one of several methods of agglomerative hierarchical clustering. At the beginning of the process, each element is in a cluster of its own. The clusters are then sequentially combined into larger clusters until all elements end up being in the same cluster. The method is also known as farthest neighbour clustering. The result of the clustering can be visualized as a dendrogram, which shows the sequence of cluster fusion and the distance at which each fusion took place. Clustering procedure At each step, the two clusters separated by the shortest distance are combined. The definition of 'shortest distance' is what differentiates between the different agglomerative clustering methods. In complete-linkage clustering, the link between two clusters contains all element pairs, and the distance between clusters equals the distance between those two elements (one in each cluster) that are farthest away from each other. The shortest of these links that rem ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Single-linkage Clustering
In statistics, single-linkage clustering is one of several methods of hierarchical clustering. It is based on grouping clusters in bottom-up fashion (agglomerative clustering), at each step combining two clusters that contain the closest pair of elements not yet belonging to the same cluster as each other. A drawback of this method is that it tends to produce long thin clusters in which nearby elements of the same cluster have small distances, but elements at opposite ends of a cluster may be much farther from each other than two elements of other clusters. This may lead to difficulties in defining classes that could usefully subdivide the data. Overview of agglomerative clustering methods In the beginning of the agglomerative clustering process, each element is in a cluster of its own. The clusters are then sequentially combined into larger clusters, until all elements end up being in the same cluster. At each step, the two clusters separated by the shortest distance are combi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Adjacency Matrix
In graph theory and computer science, an adjacency matrix is a square matrix used to represent a finite graph. The elements of the matrix indicate whether pairs of vertices are adjacent or not in the graph. In the special case of a finite simple graph, the adjacency matrix is a (0,1)-matrix with zeros on its diagonal. If the graph is undirected (i.e. all of its edges are bidirectional), the adjacency matrix is symmetric. The relationship between a graph and the eigenvalues and eigenvectors of its adjacency matrix is studied in spectral graph theory. The adjacency matrix of a graph should be distinguished from its incidence matrix, a different matrix representation whose elements indicate whether vertex–edge pairs are incident or not, and its degree matrix, which contains information about the degree of each vertex. Definition For a simple graph with vertex set , the adjacency matrix is a square matrix such that its element is one when there is an edge from vertex to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |