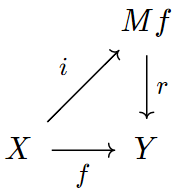|
Cofibration
In mathematics, in particular homotopy theory, a continuous mapping :i: A \to X, where A and X are topological spaces, is a cofibration if it lets homotopy classes of maps ,S/math> be extended to homotopy classes of maps ,S/math> whenever a map f \in \text_(A,S) can be extended to a map f' \in \text_(X,S) where f'\circ i = f, hence their associated homotopy classes are equal = '\circ i/math>. This type of structure can be encoded with the technical condition of having the homotopy extension property with respect to all spaces S. This definition is dual to that of a fibration, which is required to satisfy the homotopy lifting property with respect to all spaces. This duality is informally referred to as Eckmann–Hilton duality. Because of the generality this technical condition is stated, it can be used in model categories. Definition Homotopy theory In what follows, let I = ,1/math> denote the unit interval. A map i\colon A \to X of topological spaces is called a cof ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Model Category
In mathematics, particularly in homotopy theory, a model category is a category with distinguished classes of morphisms ('arrows') called ' weak equivalences', ' fibrations' and 'cofibrations' satisfying certain axioms relating them. These abstract from the category of topological spaces or of chain complexes (derived category theory). The concept was introduced by . In recent decades, the language of model categories has been used in some parts of algebraic ''K''-theory and algebraic geometry, where homotopy-theoretic approaches led to deep results. Motivation Model categories can provide a natural setting for homotopy theory: the category of topological spaces is a model category, with the homotopy corresponding to the usual theory. Similarly, objects that are thought of as spaces often admit a model category structure, such as the category of simplicial sets. Another model category is the category of chain complexes of ''R''-modules for a commutative ring ''R''. Homotopy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cofibration Diagram
In mathematics, in particular homotopy theory, a continuous mapping :i: A \to X, where A and X are topological spaces, is a cofibration if it lets homotopy classes of maps ,S/math> be extended to homotopy classes of maps ,S/math> whenever a map f \in \text_(A,S) can be extended to a map f' \in \text_(X,S) where f'\circ i = f, hence their associated homotopy classes are equal = '\circ i/math>. This type of structure can be encoded with the technical condition of having the homotopy extension property with respect to all spaces S. This definition is dual to that of a fibration, which is required to satisfy the homotopy lifting property with respect to all spaces. This duality is informally referred to as Eckmann–Hilton duality. Because of the generality this technical condition is stated, it can be used in model categories. Definition Homotopy theory In what follows, let I = ,1/math> denote the unit interval. A map i\colon A \to X of topological spaces is called a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mapping Cylinder
In mathematics, specifically algebraic topology, the mapping cylinder of a continuous function f between topological spaces X and Y is the quotient :M_f = (( ,1times X) \amalg Y)\,/\,\sim where the \amalg denotes the disjoint union, and ∼ is the equivalence relation generated by :(0,x)\sim f(x)\quad\textx\in X. That is, the mapping cylinder M_f is obtained by gluing one end of X\times ,1/math> to Y via the map f. Notice that the "top" of the cylinder \\times X is homeomorphic to X, while the "bottom" is the space f(X)\subset Y. It is common to write Mf for M_f, and to use the notation \sqcup_f or \cup_f for the mapping cylinder construction. That is, one writes :Mf = ( ,1times X) \cup_f Y with the subscripted cup symbol denoting the equivalence. The mapping cylinder is commonly used to construct the mapping cone Cf, obtained by collapsing one end of the cylinder to a point. Mapping cylinders are central to the definition of cofibrations. Basic properties The bottom ''Y'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Deformation Retract
In topology, a branch of mathematics, a retraction is a continuous mapping from a topological space into a subspace that preserves the position of all points in that subspace. The subspace is then called a retract of the original space. A deformation retraction is a mapping that captures the idea of ''continuously shrinking'' a space into a subspace. An absolute neighborhood retract (ANR) is a particularly well-behaved type of topological space. For example, every topological manifold is an ANR. Every ANR has the homotopy type of a very simple topological space, a CW complex. Definitions Retract Let ''X'' be a topological space and ''A'' a subspace of ''X''. Then a continuous map :r\colon X \to A is a retraction if the restriction of ''r'' to ''A'' is the identity map on ''A''; that is, r(a) = a for all ''a'' in ''A''. Equivalently, denoting by :\iota\colon A \hookrightarrow X the inclusion, a retraction is a continuous map ''r'' such that :r \circ \iota = \operatorname_A, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homotopy Extension Property
In mathematics, in the area of algebraic topology, the homotopy extension property indicates which homotopies defined on a subspace can be extended to a homotopy defined on a larger space. The homotopy extension property of cofibrations is dual to the homotopy lifting property that is used to define fibrations. Definition Let X\,\! be a topological space, and let A \subset X. We say that the pair (X,A)\,\! has the homotopy extension property if, given a homotopy f_t\colon A \rightarrow Y and a map \tilde_0\colon X \rightarrow Y such that \left.\tilde_0\_A = f_0, there exists an ''extension'' of f_t to a homotopy \tilde_t\colon X \rightarrow Y such that \left.\tilde_t\_A = f_t.A. Dold, ''Lectures on Algebraic Topology'', pp. 84, Springer That is, the pair (X,A)\,\! has the homotopy extension property if any map G\colon ((X\times \) \cup (A\times I)) \rightarrow Y can be extended to a map G'\colon X\times I \rightarrow Y (i.e. G\,\! and G'\,\! agree on their common domain). If ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eckmann–Hilton Duality
In the mathematical disciplines of algebraic topology and homotopy theory, Eckmann–Hilton duality in its most basic form, consists of taking a given diagram for a particular concept and reversing the direction of all arrows, much as in category theory with the idea of the opposite category. A significantly deeper form argues that the fact that the dual notion of a limit is a colimit allows us to change the Eilenberg–Steenrod axioms for homology to give axioms for cohomology. It is named after Beno Eckmann and Peter Hilton. Discussion An example is given by currying, which tells us that for any object X, a map X \times I \to Y is the same as a map X \to Y^I, where Y^I is the exponential object, given by all maps from I to Y . In the case of topological spaces, if we take I to be the unit interval, this leads to a duality between X \times I and Y^I, which then gives a duality between the reduced suspension \Sigma X, which is a quotient of X \times I, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homotopy Colimit
In mathematics, especially in algebraic topology, the homotopy limit and colimitpg 52 are variants of the notions of limit and colimit extended to the homotopy category \text(\textbf). The main idea is this: if we have a diagramF: I \to \textbfconsidered as an object in the homotopy category of diagrams F \in \text(\textbf^I), (where the homotopy equivalence of diagrams is considered pointwise), then the homotopy limit and colimits then correspond to the cone and cocone\begin \underset(F)&: * \to \textbf\\ \underset(F)&: * \to \textbf \endwhich are objects in the homotopy category \text(\textbf^*), where * is the category with one object and one morphism. Note this category is equivalent to the standard homotopy category \text(\textbf) since the latter homotopy functor category has functors which picks out an object in \text and a natural transformation corresponds to a continuous function of topological spaces. Note this construction can be generalized to model categories, whic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fibration
The notion of a fibration generalizes the notion of a fiber bundle and plays an important role in algebraic topology, a branch of mathematics. Fibrations are used, for example, in postnikov-systems or obstruction theory. In this article, all mappings are continuous mappings between topological spaces. Formal definitions Homotopy lifting property A mapping p \colon E \to B satisfies the homotopy lifting property for a space X if: * for every homotopy h \colon X \times , 1\to B and * for every mapping (also called lift) \tilde h_0 \colon X \to E lifting h, _ = h_0 (i.e. h_0 = p \circ \tilde h_0) there exists a (not necessarily unique) homotopy \tilde h \colon X \times , 1\to E lifting h (i.e. h = p \circ \tilde h) with \tilde h_0 = \tilde h, _. The following commutative diagram shows the situation:^ Fibration A fibration (also called Hurewicz fibration) is a mapping p \colon E \to B satisfying the homotopy lifting property for all spaces X. The space B is called bas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fibration
The notion of a fibration generalizes the notion of a fiber bundle and plays an important role in algebraic topology, a branch of mathematics. Fibrations are used, for example, in postnikov-systems or obstruction theory. In this article, all mappings are continuous mappings between topological spaces. Formal definitions Homotopy lifting property A mapping p \colon E \to B satisfies the homotopy lifting property for a space X if: * for every homotopy h \colon X \times , 1\to B and * for every mapping (also called lift) \tilde h_0 \colon X \to E lifting h, _ = h_0 (i.e. h_0 = p \circ \tilde h_0) there exists a (not necessarily unique) homotopy \tilde h \colon X \times , 1\to E lifting h (i.e. h = p \circ \tilde h) with \tilde h_0 = \tilde h, _. The following commutative diagram shows the situation:^ Fibration A fibration (also called Hurewicz fibration) is a mapping p \colon E \to B satisfying the homotopy lifting property for all spaces X. The space B is called bas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homotopy Theory
In mathematics, homotopy theory is a systematic study of situations in which maps can come with homotopies between them. It originated as a topic in algebraic topology but nowadays is studied as an independent discipline. Besides algebraic topology, the theory has also been used in other areas of mathematics such as algebraic geometry (e.g., A1 homotopy theory) and category theory (specifically the study of higher categories). Concepts Spaces and maps In homotopy theory and algebraic topology, the word "space" denotes a topological space. In order to avoid pathologies, one rarely works with arbitrary spaces; instead, one requires spaces to meet extra constraints, such as being compactly generated, or Hausdorff, or a CW complex. In the same vein as above, a " map" is a continuous function, possibly with some extra constraints. Often, one works with a pointed space -- that is, a space with a "distinguished point", called a basepoint. A pointed map is then a map which pre ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homotopy Colimit
In mathematics, especially in algebraic topology, the homotopy limit and colimitpg 52 are variants of the notions of limit and colimit extended to the homotopy category \text(\textbf). The main idea is this: if we have a diagramF: I \to \textbfconsidered as an object in the homotopy category of diagrams F \in \text(\textbf^I), (where the homotopy equivalence of diagrams is considered pointwise), then the homotopy limit and colimits then correspond to the cone and cocone\begin \underset(F)&: * \to \textbf\\ \underset(F)&: * \to \textbf \endwhich are objects in the homotopy category \text(\textbf^*), where * is the category with one object and one morphism. Note this category is equivalent to the standard homotopy category \text(\textbf) since the latter homotopy functor category has functors which picks out an object in \text and a natural transformation corresponds to a continuous function of topological spaces. Note this construction can be generalized to model categories, whic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homotopy Equivalence
In topology, a branch of mathematics, two continuous functions from one topological space to another are called homotopic (from grc, ὁμός "same, similar" and "place") if one can be "continuously deformed" into the other, such a deformation being called a homotopy (, ; , ) between the two functions. A notable use of homotopy is the definition of homotopy groups and cohomotopy groups, important invariants in algebraic topology. In practice, there are technical difficulties in using homotopies with certain spaces. Algebraic topologists work with compactly generated spaces, CW complexes, or spectra. Formal definition Formally, a homotopy between two continuous functions ''f'' and ''g'' from a topological space ''X'' to a topological space ''Y'' is defined to be a continuous function H: X \times ,1\to Y from the product of the space ''X'' with the unit interval , 1to ''Y'' such that H(x,0) = f(x) and H(x,1) = g(x) for all x \in X. If we think of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |