|
Clifford Module Bundle
In differential geometry, a Clifford module bundle, a bundle of Clifford modules or just Clifford module is a vector bundle whose fibers are Clifford modules, the representations of Clifford algebras. The canonical example is a spinor bundle. In fact, on a Spin manifold, every Clifford module is obtained by twisting the spinor bundle. The notion "Clifford module bundle" should not be confused with a Clifford bundle, which is a bundle of Clifford algebras. Spinor bundles Given an oriented Riemannian manifold ''M'' one can ask whether it is possible to construct a bundle of irreducible Clifford modules over ''Cℓ''(''T''*''M''). In fact, such a bundle can be constructed if and only if ''M'' is a spin manifold. Let ''M'' be an ''n''-dimensional spin manifold with spin structure ''F''Spin(''M'') → ''F''SO(''M'') on ''M''. Given any ''Cℓ''''n''R-module ''V'' one can construct the associated spinor bundle :S(M) = F_(M) \times_\sigma V\, where σ : Spin(''n'') → GL(''V'') is the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differential Geometry
Differential geometry is a mathematical discipline that studies the geometry of smooth shapes and smooth spaces, otherwise known as smooth manifolds. It uses the techniques of differential calculus, integral calculus, linear algebra and multilinear algebra. The field has its origins in the study of spherical geometry as far back as antiquity. It also relates to astronomy, the geodesy of the Earth, and later the study of hyperbolic geometry by Lobachevsky. The simplest examples of smooth spaces are the plane and space curves and surfaces in the three-dimensional Euclidean space, and the study of these shapes formed the basis for development of modern differential geometry during the 18th and 19th centuries. Since the late 19th century, differential geometry has grown into a field concerned more generally with geometric structures on differentiable manifolds. A geometric structure is one which defines some notion of size, distance, shape, volume, or other rigidifying structu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
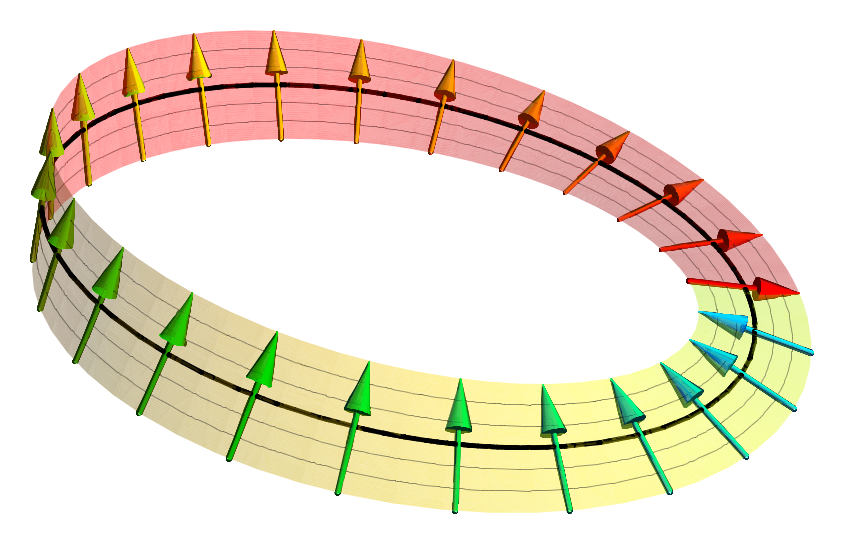
Spinor
In geometry and physics, spinors are elements of a complex vector space that can be associated with Euclidean space. Like geometric vectors and more general tensors, spinors transform linearly when the Euclidean space is subjected to a slight (infinitesimal) rotation. Unlike vectors and tensors, a spinor transforms to its negative when the space is continuously rotated through a complete turn from 0° to 360° (see picture). This property characterizes spinors: spinors can be viewed as the "square roots" of vectors (although this is inaccurate and may be misleading; they are better viewed as "square roots" of sections of vector bundles – in the case of the exterior algebra bundle of the cotangent bundle, they thus become "square roots" of differential forms). It is also possible to associate a substantially similar notion of spinor to Minkowski space, in which case the Lorentz transformations of special relativity play the role of rotations. Spinors were introduced in geome ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Structures On Manifolds
A structure is an arrangement and organization of interrelated elements in a material object or system, or the object or system so organized. Material structures include man-made objects such as buildings and machines and natural objects such as biological organisms, minerals and chemicals. Abstract structures include data structures in computer science and musical form. Types of structure include a hierarchy (a cascade of one-to-many relationships), a network featuring many-to-many links, or a lattice featuring connections between components that are neighbors in space. Load-bearing Buildings, aircraft, skeletons, anthills, beaver dams, bridges and salt domes are all examples of load-bearing structures. The results of construction are divided into buildings and non-building structures, and make up the infrastructure of a human society. Built structures are broadly divided by their varying design approaches and standards, into categories including building structures, archi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Riemannian Geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a ''Riemannian metric'', i.e. with an inner product on the tangent space at each point that varies smoothly from point to point. This gives, in particular, local notions of angle, length of curves, surface area and volume. From those, some other global quantities can be derived by integrating local contributions. Riemannian geometry originated with the vision of Bernhard Riemann expressed in his inaugural lecture "''Ueber die Hypothesen, welche der Geometrie zu Grunde liegen''" ("On the Hypotheses on which Geometry is Based.") It is a very broad and abstract generalization of the differential geometry of surfaces in R3. Development of Riemannian geometry resulted in synthesis of diverse results concerning the geometry of surfaces and the behavior of geodesics on them, with techniques that can be applied to the study of differentiable manifolds of higher dim ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Princeton University Press
Princeton University Press is an independent publisher with close connections to Princeton University. Its mission is to disseminate scholarship within academia and society at large. The press was founded by Whitney Darrow, with the financial support of Charles Scribner, as a printing press to serve the Princeton community in 1905. Its distinctive building was constructed in 1911 on William Street in Princeton. Its first book was a new 1912 edition of John Witherspoon's ''Lectures on Moral Philosophy.'' History Princeton University Press was founded in 1905 by a recent Princeton graduate, Whitney Darrow, with financial support from another Princetonian, Charles Scribner II. Darrow and Scribner purchased the equipment and assumed the operations of two already existing local publishers, that of the ''Princeton Alumni Weekly'' and the Princeton Press. The new press printed both local newspapers, university documents, ''The Daily Princetonian'', and later added book publishing to it ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Springer-Verlag
Springer Science+Business Media, commonly known as Springer, is a German multinational publishing company of books, e-books and peer-reviewed journals in science, humanities, technical and medical (STM) publishing. Originally founded in 1842 in Berlin, it expanded internationally in the 1960s, and through mergers in the 1990s and a sale to venture capitalists it fused with Wolters Kluwer and eventually became part of Springer Nature in 2015. Springer has major offices in Berlin, Heidelberg, Dordrecht, and New York City. History Julius Springer founded Springer-Verlag in Berlin in 1842 and his son Ferdinand Springer grew it from a small firm of 4 employees into Germany's then second largest academic publisher with 65 staff in 1872.Chronology ". Springer Science+Business Media. In 1964, Springer expanded its business internationally, o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spin Geometry
In mathematics, spin geometry is the area of differential geometry and topology where objects like spin manifolds and Dirac operators, and the various associated index theorems have come to play a fundamental role both in mathematics and in mathematical physics. An important generalisation is the theory of symplectic Dirac operators in symplectic spin geometry and symplectic topology, which have become important fields of mathematical research. See also * Symplectic topology * Spinor * Spinor bundle * Spin manifold In differential geometry, a spin structure on an orientable Riemannian manifold allows one to define associated spinor bundles, giving rise to the notion of a spinor in differential geometry. Spin structures have wide applications to mathematical ... Books * * Differential topology Differential geometry {{physics-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spin Representation
In mathematics, the spin representations are particular projective representations of the orthogonal group, orthogonal or special orthogonal groups in arbitrary dimension and metric signature, signature (i.e., including indefinite orthogonal groups). More precisely, they are two equivalent representation of a Lie group, representations of the spin groups, which are Double covering group, double covers of the special orthogonal groups. They are usually studied over the real number, real or complex numbers, but they can be defined over other field (mathematics), fields. Elements of a spin representation are called spinors. They play an important role in the physics, physical description of fermions such as the electron. The spin representations may be constructed in several ways, but typically the construction involves (perhaps only implicitly) the choice of a maximal isotropic subspace in the vector representation of the group. Over the real numbers, this usually requires using a co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orthonormal Frame Bundle
In mathematics, a frame bundle is a principal fiber bundle F(''E'') associated to any vector bundle ''E''. The fiber of F(''E'') over a point ''x'' is the set of all ordered bases, or ''frames'', for ''E''''x''. The general linear group acts naturally on F(''E'') via a change of basis, giving the frame bundle the structure of a principal GL(''k'', R)-bundle (where ''k'' is the rank of ''E''). The frame bundle of a smooth manifold is the one associated to its tangent bundle. For this reason it is sometimes called the tangent frame bundle. Definition and construction Let ''E'' → ''X'' be a real vector bundle of rank ''k'' over a topological space ''X''. A frame at a point ''x'' ∈ ''X'' is an ordered basis for the vector space ''E''''x''. Equivalently, a frame can be viewed as a linear isomorphism :p : \mathbf^k \to E_x. The set of all frames at ''x'', denoted ''F''''x'', has a natural right action by the general linear group GL(''k'', R) of invertible ''k'' × ''k'' matrices: a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spin Structure
In differential geometry, a spin structure on an orientable Riemannian manifold allows one to define associated spinor bundles, giving rise to the notion of a spinor in differential geometry. Spin structures have wide applications to mathematical physics, in particular to quantum field theory where they are an essential ingredient in the definition of any theory with uncharged fermions. They are also of purely mathematical interest in differential geometry, algebraic topology, and K theory. They form the foundation for spin geometry. Overview In geometry and in field theory, mathematicians ask whether or not a given oriented Riemannian manifold (''M'',''g'') admits spinors. One method for dealing with this problem is to require that ''M'' has a spin structure. This is not always possible since there is potentially a topological obstruction to the existence of spin structures. Spin structures will exist if and only if the second Stiefel–Whitney class ''w''2(''M'') ∈ H2(''M'', ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vector Bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X (for example X could be a topological space, a manifold, or an algebraic variety): to every point x of the space X we associate (or "attach") a vector space V(x) in such a way that these vector spaces fit together to form another space of the same kind as X (e.g. a topological space, manifold, or algebraic variety), which is then called a vector bundle over X. The simplest example is the case that the family of vector spaces is constant, i.e., there is a fixed vector space V such that V(x)=V for all x in X: in this case there is a copy of V for each x in X and these copies fit together to form the vector bundle X\times V over X. Such vector bundles are said to be ''trivial''. A more complicated (and prototypical) class of examples are the tangent bundles of smooth (or differentiable) manifolds: to every point of such a manifold w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spin Manifold
In differential geometry, a spin structure on an orientable Riemannian manifold allows one to define associated spinor bundles, giving rise to the notion of a spinor in differential geometry. Spin structures have wide applications to mathematical physics, in particular to quantum field theory where they are an essential ingredient in the definition of any theory with uncharged fermions. They are also of purely mathematical interest in differential geometry, algebraic topology, and K theory. They form the foundation for spin geometry. Overview In geometry and in field theory, mathematicians ask whether or not a given oriented Riemannian manifold (''M'',''g'') admits spinors. One method for dealing with this problem is to require that ''M'' has a spin structure. This is not always possible since there is potentially a topological obstruction to the existence of spin structures. Spin structures will exist if and only if the second Stiefel–Whitney class ''w''2(''M'') ∈ H2(''M'', ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |