|
Clifford Module
In mathematics, a Clifford module is a representation of a Clifford algebra. In general a Clifford algebra ''C'' is a central simple algebra over some field extension ''L'' of the field ''K'' over which the quadratic form ''Q'' defining ''C'' is defined. The abstract theory of Clifford modules was founded by a paper of M. F. Atiyah, R. Bott and Arnold S. Shapiro. A fundamental result on Clifford modules is that the Morita equivalence class of a Clifford algebra (the equivalence class of the category of Clifford modules over it) depends only on the signature . This is an algebraic form of Bott periodicity. Matrix representations of real Clifford algebras We will need to study ''anticommuting'' matrices () because in Clifford algebras orthogonal vectors anticommute : A \cdot B = \frac( AB + BA ) = 0. For the real Clifford algebra \mathbb_, we need mutually anticommuting matrices, of which ''p'' have +1 as square and ''q'' have −1 as square. : \begin \gamma_a^2 &=& +1 &\mbox &1 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matrix (mathematics)
In mathematics, a matrix (plural matrices) is a rectangular array or table of numbers, symbols, or expressions, arranged in rows and columns, which is used to represent a mathematical object or a property of such an object. For example, \begin1 & 9 & -13 \\20 & 5 & -6 \end is a matrix with two rows and three columns. This is often referred to as a "two by three matrix", a "-matrix", or a matrix of dimension . Without further specifications, matrices represent linear maps, and allow explicit computations in linear algebra. Therefore, the study of matrices is a large part of linear algebra, and most properties and operations of abstract linear algebra can be expressed in terms of matrices. For example, matrix multiplication represents composition of linear maps. Not all matrices are related to linear algebra. This is, in particular, the case in graph theory, of incidence matrices, and adjacency matrices. ''This article focuses on matrices related to linear algebra, and, unle ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Clifford Module Bundle
In differential geometry, a Clifford module bundle, a bundle of Clifford modules or just Clifford module is a vector bundle whose fibers are Clifford modules, the representations of Clifford algebras. The canonical example is a spinor bundle. In fact, on a Spin manifold, every Clifford module is obtained by twisting the spinor bundle. The notion "Clifford module bundle" should not be confused with a Clifford bundle, which is a bundle of Clifford algebras. Spinor bundles Given an oriented Riemannian manifold ''M'' one can ask whether it is possible to construct a bundle of irreducible Clifford modules over ''Cℓ''(''T''*''M''). In fact, such a bundle can be constructed if and only if ''M'' is a spin manifold. Let ''M'' be an ''n''-dimensional spin manifold with spin structure ''F''Spin(''M'') → ''F''SO(''M'') on ''M''. Given any ''Cℓ''''n''R-module ''V'' one can construct the associated spinor bundle :S(M) = F_(M) \times_\sigma V\, where σ : Spin(''n'') → GL(''V'') is the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Higher-dimensional Gamma Matrices
In mathematical physics, higher-dimensional gamma matrices generalize to arbitrary dimension the four-dimensional Gamma matrices of Dirac, which are a mainstay of relativistic quantum mechanics. They are utilized in relativistically invariant wave equations for fermions (such as spinors) in arbitrary space-time dimensions, notably in string theory and supergravity. The Weyl–Brauer matrices provide an explicit construction of higher-dimensional gamma matrices for Weyl spinors. Gamma matrices also appear in generic settings in Riemannian geometry, particularly when a spin structure can be defined. Introduction Consider a space-time of dimension with the flat Minkowski metric, : \eta = \, \eta_\, = \text(+1, \dots, +1, -1, \dots, -1) ~, with p positive entries, q negative entries, p + q = d and . Set . The standard Dirac matrices correspond to taking and or . In higher (and lower) dimensions, one may define a group, the gamma group, behaving in the same fashion as the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Weyl–Brauer Matrices
In mathematics, particularly in the theory of spinors, the Weyl–Brauer matrices are an explicit realization of a Clifford algebra as a matrix algebra of matrices. They generalize the Pauli matrices to dimensions, and are a specific construction of higher-dimensional gamma matrices. They are named for Richard Brauer and Hermann Weyl,. and were one of the earliest systematic constructions of spinors from a representation theoretic standpoint. The matrices are formed by taking tensor products of the Pauli matrices, and the space of spinors in dimensions may then be realized as the column vectors of size on which the Weyl–Brauer matrices act. Construction Suppose that ''V'' = Rn is a Euclidean space of dimension ''n''. There is a sharp contrast in the construction of the Weyl–Brauer matrices depending on whether the dimension ''n'' is even or odd. Let = 2 (or 2+1) and suppose that the Euclidean quadratic form on is given by :q_1^2+\dots+q_k^2+p_1^2+\dots+p_k^2 ~~ (+ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sign Convention
In physics, a sign convention is a choice of the physical significance of signs (plus or minus) for a set of quantities, in a case where the choice of sign is arbitrary. "Arbitrary" here means that the same physical system can be correctly described using different choices for the signs, as long as one set of definitions is used consistently. The choices made may differ between authors. Disagreement about sign conventions is a frequent source of confusion, frustration, misunderstandings, and even outright errors in scientific work. In general, a sign convention is a special case of a choice of coordinate system for the case of one dimension. Sometimes, the term "sign convention" is used more broadly to include factors of '' i'' and 2 π, rather than just choices of sign. Relativity Metric signature In relativity, the metric signature can be either or . (Note that throughout this article we are displaying the signs of the eigenvalues of the metric in the order that presents t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
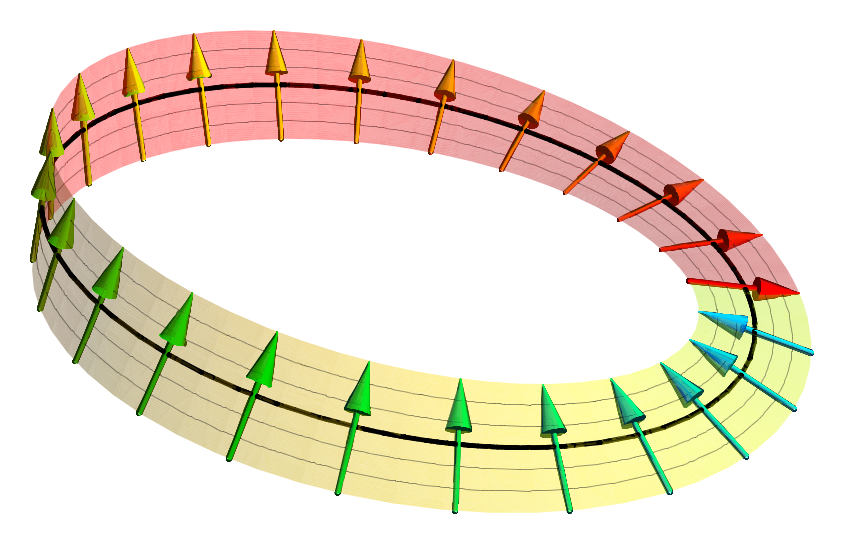
Spinors
In geometry and physics, spinors are elements of a complex vector space that can be associated with Euclidean space. Like geometric vectors and more general tensors, spinors transform linearly when the Euclidean space is subjected to a slight (infinitesimal) rotation. Unlike vectors and tensors, a spinor transforms to its negative when the space is continuously rotated through a complete turn from 0° to 360° (see picture). This property characterizes spinors: spinors can be viewed as the "square roots" of vectors (although this is inaccurate and may be misleading; they are better viewed as "square roots" of sections of vector bundles – in the case of the exterior algebra bundle of the cotangent bundle, they thus become "square roots" of differential forms). It is also possible to associate a substantially similar notion of spinor to Minkowski space, in which case the Lorentz transformations of special relativity play the role of rotations. Spinors were introduced in geome ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dirac Equation
In particle physics, the Dirac equation is a relativistic wave equation derived by British physicist Paul Dirac in 1928. In its free form, or including electromagnetic interactions, it describes all spin- massive particles, called "Dirac particles", such as electrons and quarks for which parity is a symmetry. It is consistent with both the principles of quantum mechanics and the theory of special relativity, and was the first theory to account fully for special relativity in the context of quantum mechanics. It was validated by accounting for the fine structure of the hydrogen spectrum in a completely rigorous way. The equation also implied the existence of a new form of matter, ''antimatter'', previously unsuspected and unobserved and which was experimentally confirmed several years later. It also provided a ''theoretical'' justification for the introduction of several component wave functions in Pauli's phenomenological theory of spin. The wave functions in the Dirac theo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ettore Majorana
Ettore Majorana (,, uploaded 19 April 2013, retrieved 14 December 2019 ; born on 5 August 1906 – possibly dying after 1959) was an Italian theoretical physicist who worked on neutrino masses. On 25 March 1938, he disappeared under mysterious circumstances after purchasing a ticket to travel by ship from Palermo to Naples. The Majorana equation and Majorana fermions are named after him. In 2006, the Majorana Prize was established in his memory. Life and work In 1938, Enrico Fermi was quoted as saying about Majorana: "There are several categories of scientists in the world; those of second or third rank do their best but never get very far. Then there is the first rank, those who make important discoveries, fundamental to scientific progress. But then there are the geniuses, like Galilei and Newton. Majorana was one of these." Gifted in mathematics Majorana was born in Catania, Sicily. Mathematically gifted, he was very young when he joined Enrico Fermi's team in Rome a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bott Periodicity
In mathematics, the Bott periodicity theorem describes a periodicity in the homotopy groups of classical groups, discovered by , which proved to be of foundational significance for much further research, in particular in K-theory of stable complex vector bundles, as well as the stable homotopy groups of spheres. Bott periodicity can be formulated in numerous ways, with the periodicity in question always appearing as a period-2 phenomenon, with respect to dimension, for the theory associated to the unitary group. See for example topological K-theory. There are corresponding period-8 phenomena for the matching theories, (real number, real) KO-theory and (quaternionic) KSp-theory, associated to the real orthogonal group and the quaternionic symplectic group, respectively. The J-homomorphism is a homomorphism from the homotopy groups of orthogonal groups to stable homotopy groups of spheres, which causes the period 8 Bott periodicity to be visible in the stable homotopy groups of sph ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Representation Of An Algebra
In abstract algebra, a representation of an associative algebra is a module for that algebra. Here an associative algebra is a (not necessarily unital) ring. If the algebra is not unital, it may be made so in a standard way (see the adjoint functors page); there is no essential difference between modules for the resulting unital ring, in which the identity acts by the identity mapping, and representations of the algebra. Examples Linear complex structure One of the simplest non-trivial examples is a linear complex structure, which is a representation of the complex numbers C, thought of as an associative algebra over the real numbers R. This algebra is realized concretely as \mathbb = \mathbb (x^2+1), which corresponds to . Then a representation of C is a real vector space ''V'', together with an action of C on ''V'' (a map \mathbb \to \mathrm(V)). Concretely, this is just an action of , as this generates the algebra, and the operator representing (the image of in End(''V ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Morita Equivalence
In abstract algebra, Morita equivalence is a relationship defined between rings that preserves many ring-theoretic properties. More precisely two rings like ''R'', ''S'' are Morita equivalent (denoted by R\approx S) if their categories of modules are additively equivalent (denoted by _M\approx_M). It is named after Japanese mathematician Kiiti Morita who defined equivalence and a similar notion of duality in 1958. Motivation Rings are commonly studied in terms of their modules, as modules can be viewed as representations of rings. Every ring ''R'' has a natural ''R''-module structure on itself where the module action is defined as the multiplication in the ring, so the approach via modules is more general and gives useful information. Because of this, one often studies a ring by studying the category of modules over that ring. Morita equivalence takes this viewpoint to a natural conclusion by defining rings to be Morita equivalent if their module categories are equivalent. This ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |