|
Chern Roots
In mathematics, in particular in algebraic topology, differential geometry and algebraic geometry, the Chern classes are characteristic classes associated with complex vector bundles. They have since found applications in physics, Calabi–Yau manifolds, string theory, Chern–Simons theory, knot theory, Gromov–Witten invariants, topological quantum field theory, the Chern theorem etc. Chern classes were introduced by . Geometric approach Basic idea and motivation Chern classes are characteristic classes. They are topological invariants associated with vector bundles on a smooth manifold. The question of whether two ostensibly different vector bundles are the same can be quite hard to answer. The Chern classes provide a simple test: if the Chern classes of a pair of vector bundles do not agree, then the vector bundles are different. The converse, however, is not true. In topology, differential geometry, and algebraic geometry, it is often important to count how many ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Riemann–Roch Theorem
The Riemann–Roch theorem is an important theorem in mathematics, specifically in complex analysis and algebraic geometry, for the computation of the dimension of the space of meromorphic functions with prescribed zeros and allowed poles. It relates the complex analysis of a connected compact Riemann surface with the surface's purely topological genus ''g'', in a way that can be carried over into purely algebraic settings. Initially proved as Riemann's inequality by , the theorem reached its definitive form for Riemann surfaces after work of Riemann's short-lived student . It was later generalized to algebraic curves, to higher-dimensional varieties and beyond. Preliminary notions A Riemann surface X is a topological space that is locally homeomorphic to an open subset of \Complex, the set of complex numbers. In addition, the transition maps between these open subsets are required to be holomorphic. The latter condition allows one to transfer the notions and methods of complex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
CW Complex
A CW complex (also called cellular complex or cell complex) is a kind of a topological space that is particularly important in algebraic topology. It was introduced by J. H. C. Whitehead (open access) to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial nature that allows for computation (often with a much smaller complex). The ''C'' stands for "closure-finite", and the ''W'' for "weak" topology. Definition CW complex A CW complex is constructed by taking the union of a sequence of topological spaces\emptyset = X_ \subset X_0 \subset X_1 \subset \cdotssuch that each X_k is obtained from X_ by gluing copies of k-cells (e^k_\alpha)_\alpha, each homeomorphic to D^k, to X_ by continuous gluing maps g^k_\alpha: \partial e^k_\alpha \to X_. The maps are also called attaching maps. Each X_k is called the k-skeleton of the complex. The topology of X = \cup_ X_ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homotopy
In topology, a branch of mathematics, two continuous functions from one topological space to another are called homotopic (from grc, ὁμός "same, similar" and "place") if one can be "continuously deformed" into the other, such a deformation being called a homotopy (, ; , ) between the two functions. A notable use of homotopy is the definition of homotopy groups and cohomotopy groups, important invariants in algebraic topology. In practice, there are technical difficulties in using homotopies with certain spaces. Algebraic topologists work with compactly generated spaces, CW complexes, or spectra. Formal definition Formally, a homotopy between two continuous functions ''f'' and ''g'' from a topological space ''X'' to a topological space ''Y'' is defined to be a continuous function H: X \times ,1\to Y from the product of the space ''X'' with the unit interval , 1to ''Y'' such that H(x,0) = f(x) and H(x,1) = g(x) for all x \in X. If we think of the second ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
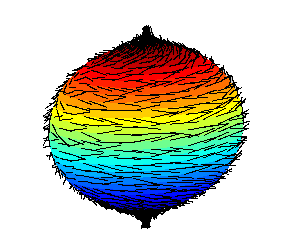
Hairy Ball Theorem
The hairy ball theorem of algebraic topology (sometimes called the hedgehog theorem in Europe) states that there is no nonvanishing continuous tangent vector field on even-dimensional ''n''-spheres. For the ordinary sphere, or 2‑sphere, if ''f'' is a continuous function that assigns a vector in R3 to every point ''p'' on a sphere such that ''f''(''p'') is always tangent to the sphere at ''p'', then there is at least one pole, a point where the field vanishes (a ''p'' such that ''f''(''p'') = 0). The theorem was first proved by Henri Poincaré for the 2-sphere in 1885, and extended to higher dimensions in 1912 by Luitzen Egbertus Jan Brouwer. The theorem has been expressed colloquially as "you can't comb a hairy ball flat without creating a cowlick" or "you can't comb the hair on a coconut". Counting zeros Every zero of a vector field has a (non-zero) " index", and it can be shown that the sum of all of the indices at all of the zeros must be two, because the Euler char ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Section (category Theory)
In category theory, a branch of mathematics, a section is a right inverse of some morphism. Dually, a retraction is a left inverse of some morphism. In other words, if f: X\to Y and g: Y\to X are morphisms whose composition f \circ g: Y\to Y is the identity morphism on Y, then g is a section of f, and f is a retraction of g. Every section is a monomorphism (every morphism with a left inverse is left-cancellative), and every retraction is an epimorphism (every morphism with a right inverse is right-cancellative). In algebra, sections are also called split monomorphisms and retractions are also called split epimorphisms. In an abelian category, if f: X\to Y is a split epimorphism with split monomorphism g: Y\to X, then X is isomorphic to the direct sum of Y and the kernel of f. The synonym coretraction for section is sometimes seen in the literature, although rarely in recent work. Properties * A section that is also an epimorphism is an isomorphism. Dually a retraction that is al ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Locally Free Sheaves
In mathematics, especially in algebraic geometry and the theory of complex manifolds, coherent sheaves are a class of sheaves closely linked to the geometric properties of the underlying space. The definition of coherent sheaves is made with reference to a sheaf of rings that codifies this geometric information. Coherent sheaves can be seen as a generalization of vector bundles. Unlike vector bundles, they form an abelian category, and so they are closed under operations such as taking kernels, images, and cokernels. The quasi-coherent sheaves are a generalization of coherent sheaves and include the locally free sheaves of infinite rank. Coherent sheaf cohomology is a powerful technique, in particular for studying the sections of a given coherent sheaf. Definitions A quasi-coherent sheaf on a ringed space (X, \mathcal O_X) is a sheaf \mathcal F of \mathcal O_X- modules which has a local presentation, that is, every point in X has an open neighborhood U in which there is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Schubert Cycle
In algebraic geometry, a Schubert variety is a certain subvariety of a Grassmannian, usually with singular points. Like a Grassmannian, it is a kind of moduli space, whose points correspond to certain kinds of subspaces ''V'', specified using linear algebra, inside a fixed vector subspace ''W''. Here ''W'' may be a vector space over an arbitrary field, though most commonly over the complex numbers. A typical example is the set ''X'' whose points correspond to those 2-dimensional subspaces ''V'' of a 4-dimensional vector space ''W'', such that ''V'' non-trivially intersects a fixed (reference) 2-dimensional subspace ''W''2: :X \ =\ \. Over the real number field, this can be pictured in usual ''xyz''-space as follows. Replacing subspaces with their corresponding projective spaces, and intersecting with an affine coordinate patch of \mathbb(W), we obtain an open subset ''X''° ⊂ ''X''. This is isomorphic to the set of all lines ''L'' (not necessarily through the origin) wh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Grassmannian
In mathematics, the Grassmannian is a space that parameterizes all -Dimension, dimensional linear subspaces of the -dimensional vector space . For example, the Grassmannian is the space of lines through the origin in , so it is the same as the projective space of one dimension lower than . When is a real or complex vector space, Grassmannians are compact space, compact smooth manifolds. In general they have the structure of a smooth algebraic variety, of dimension k(n-k). The earliest work on a non-trivial Grassmannian is due to Julius Plücker, who studied the set of projective lines in projective 3-space, equivalent to and parameterized them by what are now called Plücker coordinates. Hermann Grassmann later introduced the concept in general. Notations for the Grassmannian vary between authors; notations include , , , or to denote the Grassmannian of -dimensional subspaces of an -dimensional vector space . Motivation By giving a collection of subspaces of some vecto ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Classifying Space
In mathematics, specifically in homotopy theory, a classifying space ''BG'' of a topological group ''G'' is the quotient of a weakly contractible space ''EG'' (i.e. a topological space all of whose homotopy groups are trivial) by a proper free action of ''G''. It has the property that any ''G'' principal bundle over a paracompact manifold is isomorphic to a pullback of the principal bundle ''EG'' → ''BG''. As explained later, this means that classifying spaces represent a set-valued functor on the homotopy category of topological spaces. The term classifying space can also be used for spaces that represent a set-valued functor on the category of topological spaces, such as Sierpiński space. This notion is generalized by the notion of classifying topos. However, the rest of this article discusses the more commonly used notion of classifying space up to homotopy. For a discrete group ''G'', ''BG'' is, roughly speaking, a path-connected topological space ''X'' such that the fundam ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |