|
Hypergraphs
In mathematics, a hypergraph is a generalization of a graph in which an edge can join any number of vertices. In contrast, in an ordinary graph, an edge connects exactly two vertices. Formally, a directed hypergraph is a pair (X,E), where X is a set of elements called ''nodes'', ''vertices'', ''points'', or ''elements'' and E is a set of pairs of subsets of X. Each of these pairs (D,C)\in E is called an ''edge'' or ''hyperedge''; the vertex subset D is known as its ''tail'' or ''domain'', and C as its ''head'' or ''codomain''. The order of a hypergraph (X,E) is the number of vertices in X. The size of the hypergraph is the number of edges in E. The order of an edge e=(D,C) in a directed hypergraph is , e, = (, D, ,, C, ): that is, the number of vertices in its tail followed by the number of vertices in its head. The definition above generalizes from a directed graph to a directed hypergraph by defining the head or tail of each edge as a set of vertices (C\subseteq X or D\ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Incidence Structure
In mathematics, an incidence structure is an abstract system consisting of two types of objects and a single relationship between these types of objects. Consider the Point (geometry), points and Line (geometry), lines of the Euclidean plane as the two types of objects and ignore all the properties of this geometry except for the heterogeneous relation, relation of which points are incident (geometry), incident on which lines for all points and lines. What is left is the incidence structure of the Euclidean plane. Incidence structures are most often considered in the geometrical context where they are abstracted from, and hence generalize, planes (such as affine plane (incidence geometry), affine, projective plane, projective, and Möbius planes), but the concept is very broad and not limited to geometric settings. Even in a geometric setting, incidence structures are not limited to just points and lines; higher-dimensional objects (Plane (mathematics), planes, Solid geometry, sol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cooperative Game Theory
In game theory, a cooperative game (or coalitional game) is a game with groups of players who form binding “coalitions” with external enforcement of cooperative behavior (e.g. through contract law). This is different from non-cooperative games in which there is either no possibility to forge alliances or all agreements need to be self-enforcing (e.g. through credible threats). Cooperative games are analysed by focusing on coalitions that can be formed, and the joint actions that groups can take and the resulting collective payoffs. Mathematical definition A cooperative game is given by specifying a value for every coalition. Formally, the coalitional game consists of a finite set of players N , called the ''grand coalition'', and a ''characteristic function'' v : 2^N \to \mathbb from the set of all possible coalitions of players to a set of payments that satisfies v( \emptyset ) = 0 . The function describes how much collective payoff a set of players can gain by ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
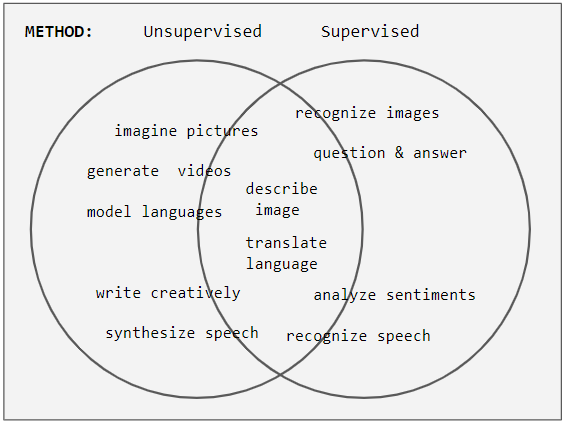
Semi-supervised Learning
Weak supervision (also known as semi-supervised learning) is a paradigm in machine learning, the relevance and notability of which increased with the advent of large language models due to large amount of data required to train them. It is characterized by using a combination of a small amount of human-labeled data (exclusively used in more expensive and time-consuming supervised learning paradigm), followed by a large amount of unlabeled data (used exclusively in unsupervised learning paradigm). In other words, the desired output values are provided only for a subset of the training data. The remaining data is unlabeled or imprecisely labeled. Intuitively, it can be seen as an exam and labeled data as sample problems that the teacher solves for the class as an aid in solving another set of problems. In the Transduction (machine learning), transductive setting, these unsolved problems act as exam questions. In the Inductive reasoning, inductive setting, they become practice problems ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spectral Graph Theory
In mathematics, spectral graph theory is the study of the properties of a Graph (discrete mathematics), graph in relationship to the characteristic polynomial, eigenvalues, and eigenvectors of matrices associated with the graph, such as its adjacency matrix or Laplacian matrix. The adjacency matrix of a simple undirected graph is a Real number, real symmetric matrix and is therefore Orthogonal diagonalization, orthogonally diagonalizable; its eigenvalues are real algebraic integers. While the adjacency matrix depends on the vertex labeling, its Spectrum of a matrix, spectrum is a graph invariant, although not a complete one. Spectral graph theory is also concerned with graph parameters that are defined via multiplicities of eigenvalues of matrices associated to the graph, such as the Colin de Verdière graph invariant, Colin de Verdière number. Cospectral graphs Two graphs are called cospectral or isospectral if the adjacency matrices of the graphs are isospectral, that is, if t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spectral Clustering
In multivariate statistics, spectral clustering techniques make use of the spectrum (eigenvalues) of the similarity matrix of the data to perform dimensionality reduction before clustering in fewer dimensions. The similarity matrix is provided as an input and consists of a quantitative assessment of the relative similarity of each pair of points in the dataset. In application to image segmentation, spectral clustering is known as segmentation-based object categorization. Definitions Given an enumerated set of data points, the similarity matrix may be defined as a symmetric matrix A, where A_\geq 0 represents a measure of the similarity between data points with indices i and j. The general approach to spectral clustering is to use a standard clustering method (there are many such methods, ''k''-means is discussed below) on relevant eigenvectors of a Laplacian matrix of A. There are many different ways to define a Laplacian which have different mathematical interpretatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bioinformatics
Bioinformatics () is an interdisciplinary field of science that develops methods and Bioinformatics software, software tools for understanding biological data, especially when the data sets are large and complex. Bioinformatics uses biology, chemistry, physics, computer science, data science, computer programming, information engineering, mathematics and statistics to analyze and interpret biological data. The process of analyzing and interpreting data can sometimes be referred to as computational biology, however this distinction between the two terms is often disputed. To some, the term ''computational biology'' refers to building and using models of biological systems. Computational, statistical, and computer programming techniques have been used for In silico, computer simulation analyses of biological queries. They include reused specific analysis "pipelines", particularly in the field of genomics, such as by the identification of genes and single nucleotide polymorphis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Image Retrieval
An image retrieval system is a computer system used for browsing, searching and retrieving images from a large database of digital images. Most traditional and common methods of image retrieval utilize some method of adding metadata such as captioning, keywords, title or descriptions to the images so that retrieval can be performed over the annotation words. Manual image annotation is time-consuming, laborious and expensive; to address this, there has been a large amount of research done on automatic image annotation. Additionally, the increase in social web applications and the semantic web have inspired the development of several web-based image annotation tools. The first microcomputer-based image database retrieval system was developed at MIT, in the 1990s, by Banireddy Prasaad, Amar Gupta, Hoo-min Toong, and Stuart Madnick. A 2008 survey article documented progresses after 2007. Search methods Image search is a specialized data search used to find images. To search for i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Recommender System
A recommender system (RecSys), or a recommendation system (sometimes replacing ''system'' with terms such as ''platform'', ''engine'', or ''algorithm'') and sometimes only called "the algorithm" or "algorithm", is a subclass of information filtering system that provides suggestions for items that are most pertinent to a particular user. Recommender systems are particularly useful when an individual needs to choose an item from a potentially overwhelming number of items that a service may offer. Modern recommendation systems such as those used on large social media sites make extensive use of AI, machine learning and related techniques to learn the behavior and preferences of each user and categorize content to tailor their feed individually. Typically, the suggestions refer to various decision-making processes, such as what product to purchase, what music to listen to, or what online news to read. Recommender systems are used in a variety of areas, with commonly recognised ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regularization (mathematics)
In mathematics, statistics, Mathematical finance, finance, and computer science, particularly in machine learning and inverse problems, regularization is a process that converts the Problem solving, answer to a problem to a simpler one. It is often used in solving ill-posed problems or to prevent overfitting. Although regularization procedures can be divided in many ways, the following delineation is particularly helpful: * Explicit regularization is regularization whenever one explicitly adds a term to the optimization problem. These terms could be Prior probability, priors, penalties, or constraints. Explicit regularization is commonly employed with ill-posed optimization problems. The regularization term, or penalty, imposes a cost on the optimization function to make the optimal solution unique. * Implicit regularization is all other forms of regularization. This includes, for example, early stopping, using a robust loss function, and discarding outliers. Implicit regularizat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Machine Learning
Machine learning (ML) is a field of study in artificial intelligence concerned with the development and study of Computational statistics, statistical algorithms that can learn from data and generalise to unseen data, and thus perform Task (computing), tasks without explicit Machine code, instructions. Within a subdiscipline in machine learning, advances in the field of deep learning have allowed Neural network (machine learning), neural networks, a class of statistical algorithms, to surpass many previous machine learning approaches in performance. ML finds application in many fields, including natural language processing, computer vision, speech recognition, email filtering, agriculture, and medicine. The application of ML to business problems is known as predictive analytics. Statistics and mathematical optimisation (mathematical programming) methods comprise the foundations of machine learning. Data mining is a related field of study, focusing on exploratory data analysi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Steiner Tree Problem
In combinatorial mathematics, the Steiner tree problem, or minimum Steiner tree problem, named after Jakob Steiner, is an umbrella term for a class of problems in combinatorial optimization. While Steiner tree problems may be formulated in a number of settings, they all require an optimal interconnect for a given set of objects and a predefined objective function. One well-known variant, which is often used synonymously with the term Steiner tree problem, is the Steiner tree problem in graphs. Given an undirected graph with non-negative edge weights and a subset of vertices, usually referred to as terminals, the Steiner tree problem in graphs requires a tree of minimum weight that contains all terminals (but may include additional vertices) and minimizes the total weight of its edges. Further well-known variants are the ''Euclidean Steiner tree problem'' and the '' rectilinear minimum Steiner tree problem''. The Steiner tree problem in graphs can be seen as a generalization ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |