|
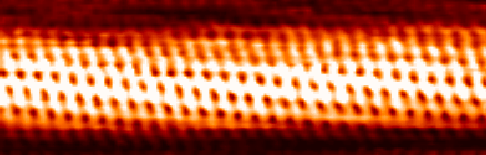
Cylinder Sphere Packing
Sphere packing in a cylinder is a three-dimensional packing problem with the objective of packing a given number of identical spheres inside a cylinder of specified diameter and length. For cylinders with diameters on the same order of magnitude as the spheres, such packings result in what are called columnar structures. These problems are studied extensively in the context of biology, nanoscience, materials science, and so forth due to the analogous assembly of small particles (like cells and atoms) into cylindrical crystalline structures. The book "Columnar Structures of Spheres: Fundamentals and Applications" serves as a notable contributions to this field of study. Authored by Winkelmann and Chan, the book reviews theoretical foundations and practical applications of densely packed spheres within cylindrical confinements. Appearance in science Columnar structures appear in various research fields on a broad range of length scales from metres down to the nanoscale. On the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Notochord
The notochord is an elastic, rod-like structure found in chordates. In vertebrates the notochord is an embryonic structure that disintegrates, as the vertebrae develop, to become the nucleus pulposus in the intervertebral discs of the vertebral column. In non-vertebrate chordates a notochord persists. The notochord is derived from the embryonic mesoderm and consists of an inner core of vacuolated cells filled with glycoproteins, covered by two helical collagen-elastin sheaths. It lies longitudinally along the rostral-caudal (head to tail) axis of the body, dorsal to the gut tube, and ventral to the dorsal nerve cord. Some chordate invertebrates, such as tunicates, develop a notochord during the larval stage but lose it through subsequent stages into adulthood. The notochord is important for signaling the dorso-ventral patterning of cells coming from the mesodermal progenitors. This helps form the precursors needed for certain organs and the embryo to develop ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Nanotubes
A carbon nanotube (CNT) is a tube made of carbon with a diameter in the nanometre range (nanoscale). They are one of the allotropes of carbon. Two broad classes of carbon nanotubes are recognized: * ''Single-walled carbon nanotubes'' (''SWCNTs'') have diameters around 0.5–2.0 nanometres, about 100,000 times smaller than the width of a human hair. They can be idealised as cutouts from a two-dimensional graphene sheet rolled up to form a hollow cylinder. * ''Multi-walled carbon nanotubes'' (''MWCNTs'') consist of nested single-wall carbon nanotubes in a nested, tube-in-tube structure. Double- and triple-walled carbon nanotubes are special cases of MWCNT. Carbon nanotubes can exhibit remarkable properties, such as exceptional tensile strength and thermal conductivity because of their nanostructure and strength of the bonds between carbon atoms. Some SWCNT structures exhibit high electrical conductivity while others are semiconductors. In addition, carbon nanotubes can be chem ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
CT Scan
A computed tomography scan (CT scan), formerly called computed axial tomography scan (CAT scan), is a medical imaging technique used to obtain detailed internal images of the body. The personnel that perform CT scans are called radiographers or radiology technologists. CT scanners use a rotating X-ray tube and a row of detectors placed in a gantry (medical), gantry to measure X-ray Attenuation#Radiography, attenuations by different tissues inside the body. The multiple X-ray measurements taken from different angles are then processed on a computer using tomographic reconstruction algorithms to produce Tomography, tomographic (cross-sectional) images (virtual "slices") of a body. CT scans can be used in patients with metallic implants or pacemakers, for whom magnetic resonance imaging (MRI) is Contraindication, contraindicated. Since its development in the 1970s, CT scanning has proven to be a versatile imaging technique. While CT is most prominently used in medical diagnosis, i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
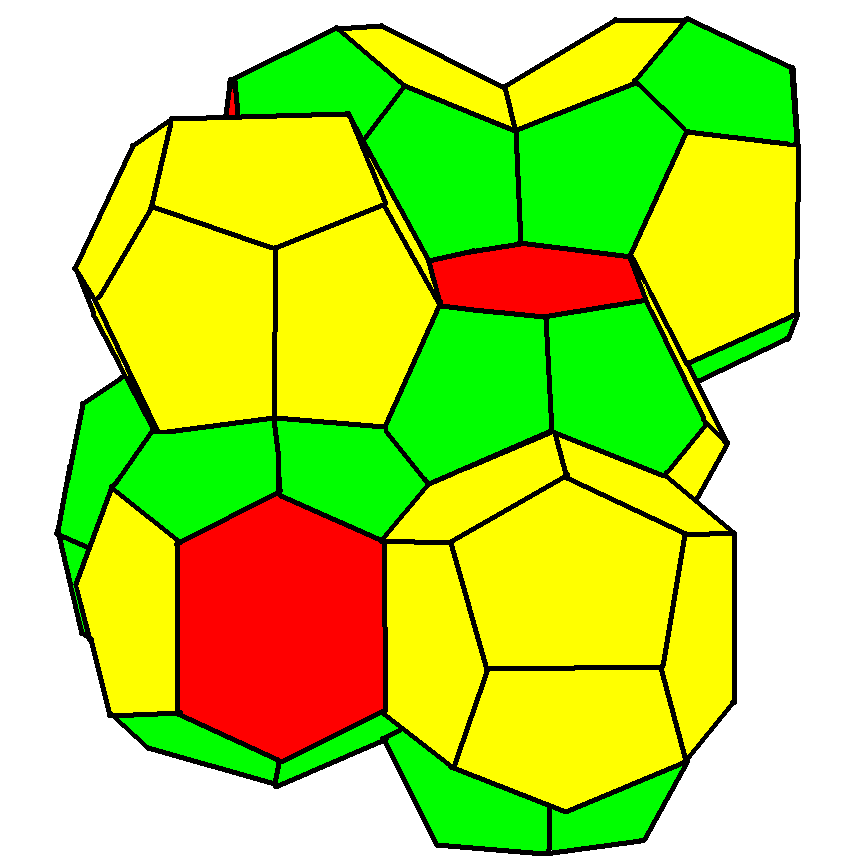
Weaire–Phelan Structure
In geometry, the Weaire–Phelan structure is a three-dimensional structure representing an idealised foam of equal-sized bubbles, with two different shapes. In 1993, Denis Weaire and Robert Phelan found that this structure was a better solution of the Kelvin problem of tiling space by equal volume cells of minimum surface area than the previous best-known solution, the Kelvin structure. History and the Kelvin problem In two dimensions, the subdivision of the plane into cells of equal area with minimum average perimeter is given by the hexagonal tiling, but although the first record of this honeycomb conjecture goes back to the ancient Roman scholar Marcus Terentius Varro (116-27 BCE), it was not proven until the work of Thomas C. Hales in 1999. In 1887, Lord Kelvin asked the corresponding question for three-dimensional space: how can space be partitioned into cells of equal volume with the least area of surface between them? Or, in short, what was the most efficient soap bubbl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Dodecahedron
In geometry, a dodecahedron (; ) or duodecahedron is any polyhedron with twelve flat faces. The most familiar dodecahedron is the regular dodecahedron with regular pentagons as faces, which is a Platonic solid. There are also three Kepler–Poinsot polyhedron, regular star dodecahedra, which are constructed as stellations of the convex form. All of these have icosahedral symmetry, order 120. Some dodecahedra have the same combinatorial structure as the regular dodecahedron (in terms of the graph formed by its vertices and edges), but their pentagonal faces are not regular: The #Pyritohedron, pyritohedron, a common crystal form in pyrite, has pyritohedral symmetry, while the #Tetartoid, tetartoid has tetrahedral symmetry. The rhombic dodecahedron can be seen as a limiting case of the pyritohedron, and it has octahedral symmetry. The elongated dodecahedron and trapezo-rhombic dodecahedron variations, along with the rhombic dodecahedra, are space-filling polyhedra, space-filling. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Cylinder Sphere Packing
Sphere packing in a cylinder is a three-dimensional packing problem with the objective of packing a given number of identical spheres inside a cylinder of specified diameter and length. For cylinders with diameters on the same order of magnitude as the spheres, such packings result in what are called columnar structures. These problems are studied extensively in the context of biology, nanoscience, materials science, and so forth due to the analogous assembly of small particles (like cells and atoms) into cylindrical crystalline structures. The book "Columnar Structures of Spheres: Fundamentals and Applications" serves as a notable contributions to this field of study. Authored by Winkelmann and Chan, the book reviews theoretical foundations and practical applications of densely packed spheres within cylindrical confinements. Appearance in science Columnar structures appear in various research fields on a broad range of length scales from metres down to the nanoscale. On the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Hard Spheres
Hard spheres are widely used as model particles in the statistical mechanical theory of fluids and solids. They are defined simply as impenetrable spheres that cannot overlap in space. They mimic the extremely strong ("infinitely elastic bouncing") repulsion that atoms and spherical molecules experience at very close distances. Hard spheres systems are studied by analytical means, by molecular dynamics simulations, and by the experimental study of certain colloidal model systems. Beside being a model of theoretical significance, the hard-sphere system is used as a basis in the formulation of several modern, predictive Equations of State for real fluids through the SAFT approach, and models for transport properties in gases through Chapman-Enskog Theory. Formal definition Hard spheres of diameter \sigma are particles with the following pairwise interaction potential: V(\mathbf_1, \mathbf_2) = \begin 0 & \text \quad , \mathbf_1-\mathbf_2, \geq \sigma \\ \infty & \text \qu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Surface Evolver
Surface Evolver is an interactive program for the study of surfaces shaped by surface tension and other energies, and subject to various constraints. A surface is implemented as a simplicial complex. The user defines an initial surface in a datafile. The Evolver evolves the surface toward minimal energy by a gradient descent method. The aim can be to find a minimal energy surface, or to model the process of evolution by mean curvature. The energy in the Evolver can be a combination of surface tension, gravitational energy, squared mean curvature, user-defined surface integrals, or knot energies. The Evolver can handle arbitrary topology, volume constraints, boundary constraints, boundary contact angles, prescribed mean curvature, crystalline integrands, gravity, and constraints expressed as surface integrals. The surface can be in an ambient space of arbitrary dimension, which can have a Riemannian metric, and the ambient space can be a quotient space under a group action. Ev ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Polyhedron
In geometry, a polyhedron (: polyhedra or polyhedrons; ) is a three-dimensional figure with flat polygonal Face (geometry), faces, straight Edge (geometry), edges and sharp corners or Vertex (geometry), vertices. The term "polyhedron" may refer either to a solid figure or to its boundary surface (mathematics), surface. The terms solid polyhedron and polyhedral surface are commonly used to distinguish the two concepts. Also, the term ''polyhedron'' is often used to refer implicitly to the whole structure (mathematics), structure formed by a solid polyhedron, its polyhedral surface, its faces, its edges, and its vertices. There are many definitions of polyhedron. Nevertheless, the polyhedron is typically understood as a generalization of a two-dimensional polygon and a three-dimensional specialization of a polytope, a more general concept in any number of dimensions. Polyhedra have several general characteristics that include the number of faces, topological classification by Eule ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Columnar Structure Of A Foam
Epithelium or epithelial tissue is a thin, continuous, protective layer of cells with little extracellular matrix. An example is the epidermis, the outermost layer of the skin. Epithelial (mesothelial) tissues line the outer surfaces of many internal organs, the corresponding inner surfaces of body cavities, and the inner surfaces of blood vessels. Epithelial tissue is one of the four basic types of animal tissue, along with connective tissue, muscle tissue and nervous tissue. These tissues also lack blood or lymph supply. The tissue is supplied by nerves. There are three principal shapes of epithelial cell: squamous (scaly), columnar, and cuboidal. These can be arranged in a singular layer of cells as simple epithelium, either simple squamous, simple columnar, or simple cuboidal, or in layers of two or more cells deep as stratified (layered), or ''compound'', either squamous, columnar or cuboidal. In some tissues, a layer of columnar cells may appear to be stratified due to t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Callistemon
''Callistemon'' is a genus of shrubs in the family Myrtaceae, first described as a genus in 1814. The entire genus is endemic to Australia but widely cultivated in many other regions and naturalised in scattered locations. Their status as a separate taxon is in doubt, some authorities accepting that the difference between callistemons and melaleucas is not sufficient for them to be grouped in a separate genus. Description ''Callistemon'' species have commonly been referred to as bottlebrushes because of their cylindrical, brush like flowers resembling a traditional bottle brush. They are mostly found in the more temperate regions of Australia, especially along the east coast and typically favour moist conditions so when planted in gardens thrive on regular watering. However, two species are found in Tasmania and several others in the south-west of Western Australia. At least some species are drought-resistant and some are used in ornamental landscaping elsewhere in the world. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |