|
Cross Slip
Cross slip is the process by which a screw dislocation moves from one slip plane to another due to local stresses. It allows non-planar movement of screw dislocations. Non-planar movement of edge dislocations is achieved through climb. Since the Burgers vector of a perfect screw dislocation is parallel to the dislocation line, it has an infinite number of possible slip planes (planes containing the dislocation line and the Burgers vector), unlike an edge or mixed dislocation, which has a unique slip plane. Therefore, a screw dislocation can glide or slip along any plane that contains its Burgers vector. During cross slip, the screw dislocation switches from gliding along one slip plane to gliding along a different slip plane, called the cross-slip plane. The cross slip of moving dislocations can be seen by transmission electron microscopy. Mechanisms The possible cross-slip planes are determined by the crystal system. In body centered cubic (BCC) metals, a screw dislocation wi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cross Slip
Cross slip is the process by which a screw dislocation moves from one slip plane to another due to local stresses. It allows non-planar movement of screw dislocations. Non-planar movement of edge dislocations is achieved through climb. Since the Burgers vector of a perfect screw dislocation is parallel to the dislocation line, it has an infinite number of possible slip planes (planes containing the dislocation line and the Burgers vector), unlike an edge or mixed dislocation, which has a unique slip plane. Therefore, a screw dislocation can glide or slip along any plane that contains its Burgers vector. During cross slip, the screw dislocation switches from gliding along one slip plane to gliding along a different slip plane, called the cross-slip plane. The cross slip of moving dislocations can be seen by transmission electron microscopy. Mechanisms The possible cross-slip planes are determined by the crystal system. In body centered cubic (BCC) metals, a screw dislocation wi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Plasticity (physics)
In physics and materials science, plasticity, also known as plastic deformation, is the ability of a solid material to undergo permanent Deformation (engineering), deformation, a non-reversible change of shape in response to applied forces. For example, a solid piece of metal being bent or pounded into a new shape displays plasticity as permanent changes occur within the material itself. In engineering, the transition from Elasticity (physics), elastic behavior to plastic behavior is known as Yield (engineering), yielding. Plastic deformation is observed in most materials, particularly metals, soils, Rock (geology), rocks, concrete, and foams. However, the physical mechanisms that cause plastic deformation can vary widely. At a crystalline scale, plasticity in metals is usually a consequence of dislocations. Such defects are relatively rare in most crystalline materials, but are numerous in some and part of their crystal structure; in such cases, plastic crystallinity can res ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Miller Index
Miller indices form a notation system in crystallography for lattice planes in crystal (Bravais) lattices. In particular, a family of lattice planes of a given (direct) Bravais lattice is determined by three integers ''h'', ''k'', and ''ℓ'', the ''Miller indices''. They are written (hkℓ), and denote the family of (parallel) lattice planes (of the given Bravais lattice) orthogonal to \mathbf_ = h\mathbf + k\mathbf + \ell\mathbf, where \mathbf are the basis or primitive translation vectors of the reciprocal lattice for the given Bravais lattice. (Note that the plane is not always orthogonal to the linear combination of direct or original lattice vectors h\mathbf + k\mathbf + \ell\mathbf because the direct lattice vectors need not be mutually orthogonal.) This is based on the fact that a reciprocal lattice vector \mathbf (the vector indicating a reciprocal lattice point from the reciprocal lattice origin) is the wavevector of a plane wave in the Fourier series of a spatial ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Deformation (engineering)
In engineering, deformation refers to the change in size or shape of an object. ''Displacements'' are the ''absolute'' change in position of a point on the object. Deflection is the relative change in external displacements on an object. Strain is the ''relative'' internal change in shape of an infinitesimally small cube of material and can be expressed as a non-dimensional change in length or angle of distortion of the cube. Strains are related to the forces acting on the cube, which are known as stress, by a stress-strain curve. The relationship between stress and strain is generally linear and reversible up until the yield point and the deformation is elastic. The linear relationship for a material is known as Young's modulus. Above the yield point, some degree of permanent distortion remains after unloading and is termed plastic deformation. The determination of the stress and strain throughout a solid object is given by the field of strength of materials and for a structure ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Recovery (metallurgy)
Recovery is a process by which deformed grains can reduce their stored energy by the removal or rearrangement of defects in their crystal structure. These defects, primarily dislocations, are introduced by plastic deformation of the material and act to increase the yield strength of a material. Since recovery reduces the dislocation density the process is normally accompanied by a reduction in a material's strength and a simultaneous increase in the ductility. As a result, recovery may be considered beneficial or detrimental depending on the circumstances. Recovery is related to the similar process of recrystallization and grain growth, each of them being stages of annealing. Recovery competes with recrystallization, as both are driven by the stored energy, but is also thought to be a necessary prerequisite for the nucleation of recrystallized grains. It is so called because there is a recovery of the electrical conductivity due to a reduction in dislocations. This creates defect ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
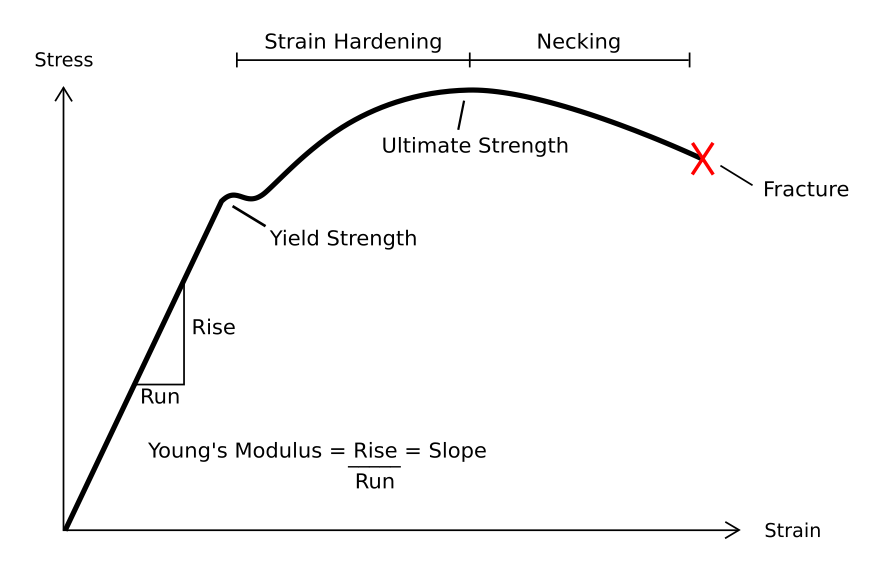
Flow Stress
In materials science the flow stress, typically denoted as Yf (or \sigma_\text), is defined as the instantaneous value of stress required to continue plastically deforming a material - to keep it flowing. It is most commonly, though not exclusively, used in reference to metals. On a stress-strain curve, the flow stress can be found anywhere within the plastic regime; more explicitly, a flow stress can be found for any value of strain between and including yield point (\sigma_\text) and excluding fracture (\sigma_\text): \sigma_\text \leq Y_\text < \sigma_\text. The flow stress changes as deformation proceeds and usually increases as strain accumulates due to , although the flow stress could decrease due to any recovery process. In continuum ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Work Hardening
In materials science, work hardening, also known as strain hardening, is the strengthening of a metal or polymer by plastic deformation. Work hardening may be desirable, undesirable, or inconsequential, depending on the context. This strengthening occurs because of dislocation movements and dislocation generation within the crystal structure of the material. Many non-brittle metals with a reasonably high melting point as well as several polymers can be strengthened in this fashion. Alloys not amenable to heat treatment, including low-carbon steel, are often work-hardened. Some materials cannot be work-hardened at low temperatures, such as indium, however others can be strengthened only via work hardening, such as pure copper and aluminum. Undesirable work hardening An example of undesirable work hardening is during machining when early passes of a cutter inadvertently work-harden the workpiece surface, causing damage to the cutter during the later passes. Certain alloys are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Solid Solution Strengthening
In metallurgy, solid solution strengthening is a type of alloying that can be used to improve the strength of a pure metal. The technique works by adding atoms of one element (the alloying element) to the crystalline lattice of another element (the base metal), forming a solid solution. The local nonuniformity in the lattice due to the alloying element makes plastic deformation more difficult by impeding dislocation motion through stress fields. In contrast, alloying beyond the solubility limit can form a second phase, leading to strengthening via other mechanisms (e.g. the precipitation of intermetallic compounds). Types Depending on the size of the alloying element, a substitutional solid solution or an interstitial solid solution can form. In both cases, atoms are vizualised as rigid spheres where the overall crystal structure is essentially unchanged. The rationale of crystal geometry to atom solubility prediction is summarized in the Hume-Rothery rules and Pauling's rules. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Yield Stress
In materials science and engineering, the yield point is the point on a stress-strain curve that indicates the limit of elastic behavior and the beginning of plastic behavior. Below the yield point, a material will deform elastically and will return to its original shape when the applied stress is removed. Once the yield point is passed, some fraction of the deformation will be permanent and non-reversible and is known as plastic deformation. The yield strength or yield stress is a material property and is the stress corresponding to the yield point at which the material begins to deform plastically. The yield strength is often used to determine the maximum allowable load in a mechanical component, since it represents the upper limit to forces that can be applied without producing permanent deformation. In some materials, such as aluminium, there is a gradual onset of non-linear behavior, making the precise yield point difficult to determine. In such a case, the offset yiel ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Dislocation
In materials science, a partial dislocation is a decomposed form of dislocation that occurs within a crystalline material. An ''extended dislocation'' is a dislocation that has dissociated into a pair of partial dislocations. The vector sum of the Burgers vectors of the partial dislocations is the Burgers vector of the extended dislocation. Reaction favorability A dislocation will decompose into partial dislocations if the energy state of the sum of the partials is less than the energy state of the original dislocation. This is summarized by ''Frank's Energy Criterion'': : \begin , \boldsymbol, ^2>&, \boldsymbol, ^2+, \boldsymbol, ^2 \text\\ , \boldsymbol, ^2& , \frac \sqrt, ^2+, \frac \sqrt, ^2\\ \frac >& \frac+\frac \end The components of the ''Shockley Partials'' must add up to the original vector that is being decomposed: : \begin \frac (1) =& \frac(2)+\frac(1)\\ \frac (0) =& \frac(-1)+\frac(1)\\ \frac (-1) =& \frac(-1)+\frac(-2) \end Frank partial dislocations ''Frank ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dislocation
In materials science, a dislocation or Taylor's dislocation is a linear crystallographic defect or irregularity within a crystal structure that contains an abrupt change in the arrangement of atoms. The movement of dislocations allow atoms to slide over each other at low stress levels and is known as ''glide'' or slip. The crystalline order is restored on either side of a ''glide dislocation'' but the atoms on one side have moved by one position. The crystalline order is not fully restored with a ''partial dislocation''. A dislocation defines the boundary between ''slipped'' and ''unslipped'' regions of material and as a result, must either form a complete loop, intersect other dislocations or defects, or extend to the edges of the crystal. A dislocation can be characterised by the distance and direction of movement it causes to atoms which is defined by the Burgers vector. Plastic deformation of a material occurs by the creation and movement of many dislocations. The number and a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
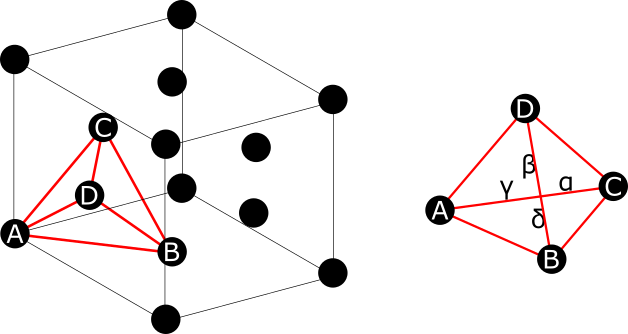
Cubic Crystal System
In crystallography, the cubic (or isometric) crystal system is a crystal system where the Crystal_structure#Unit_cell, unit cell is in the shape of a cube. This is one of the most common and simplest shapes found in crystals and minerals. There are three main varieties of these crystals: *Primitive cubic (abbreviated ''cP'' and alternatively called simple cubic) *Body-centered cubic (abbreviated ''cI'' or bcc) *Face-centered cubic (abbreviated ''cF'' or fcc, and alternatively called Close-packing_of_equal_spheres, ''cubic close-packed'' or ccp) Each is subdivided into other variants listed below. Although the ''unit cells'' in these crystals are conventionally taken to be cubes, the primitive_cell, primitive unit cells often are not. Bravais lattices The three Bravais lattices in the cubic crystal system are: The primitive cubic lattice (cP) consists of one Lattice_(group), lattice point on each corner of the cube; this means each simple cubic unit cell has in total one latt ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |