|
Critical Exponents (phase Transitions)
Critical exponents describe the behavior of physical quantities near continuous phase transitions. It is believed, though not proven, that they are universal, i.e. they do not depend on the details of the physical system, but only on some of its general features. For instance, for ferromagnetic systems at thermal equilibrium, the critical exponents depend only on: * the dimension of the system * the range of the interaction * the spin dimension These properties of critical exponents are supported by experimental data. Analytical results can be theoretically achieved in mean field theory in high dimensions or when exact solutions are known such as the two-dimensional Ising model. The theoretical treatment in generic dimensions requires the renormalization group approach or, for systems at thermal equilibrium, the conformal bootstrap techniques. Phase transitions and critical exponents appear in many physical systems such as water at the critical point, in magnetic systems, in s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Phase Transitions
In physics, chemistry, and other related fields like biology, a phase transition (or phase change) is the physical process of transition between one state of a medium and another. Commonly the term is used to refer to changes among the basic State of matter, states of matter: solid, liquid, and gas, and in rare cases, plasma (physics), plasma. A phase of a thermodynamic system and the states of matter have uniform physical property, physical properties. During a phase transition of a given medium, certain properties of the medium change as a result of the change of external conditions, such as temperature or pressure. This can be a discontinuous change; for example, a liquid may become gas upon heating to its boiling point, resulting in an abrupt change in volume. The identification of the external conditions at which a transformation occurs defines the phase transition point. Types of phase transition States of matter Phase transitions commonly refer to when a substance tran ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thermodynamic Free Energy
In thermodynamics, the thermodynamic free energy is one of the state functions of a thermodynamic system. The change in the free energy is the maximum amount of work that the system can perform in a process at constant temperature, and its sign indicates whether the process is thermodynamically favorable or forbidden. Since free energy usually contains potential energy, it is not absolute but depends on the choice of a zero point. Therefore, only relative free energy values, or changes in free energy, are physically meaningful. The free energy is the portion of any first-law energy that is available to perform thermodynamic work at constant temperature, ''i.e.'', work mediated by thermal energy. Free energy is subject to irreversible loss in the course of such work. Since first-law energy is always conserved, it is evident that free energy is an expendable, second-law kind of energy. Several free energy functions may be formulated based on system criteria. Free energy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ginzburg–Landau Theory
In physics, Ginzburg–Landau theory, often called Landau–Ginzburg theory, named after Vitaly Ginzburg and Lev Landau, is a mathematical physical theory used to describe superconductivity. In its initial form, it was postulated as a phenomenological model which could describe type-I superconductors without examining their microscopic properties. One GL-type superconductor is the famous YBCO, and generally all cuprates. Later, a version of Ginzburg–Landau theory was derived from the Bardeen–Cooper–Schrieffer microscopic theory by Lev Gor'kov, thus showing that it also appears in some limit of microscopic theory and giving microscopic interpretation of all its parameters. The theory can also be given a general geometric setting, placing it in the context of Riemannian geometry, where in many cases exact solutions can be given. This general setting then extends to quantum field theory and string theory, again owing to its solvability, and its close relation to other, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Landau Theory
Landau theory (also known as Ginzburg–Landau theory, despite the confusing name) in physics is a theory that Lev Landau introduced in an attempt to formulate a general theory of continuous (i.e., second-order) phase transitions. It can also be adapted to systems under externally-applied fields, and used as a quantitative model for discontinuous (i.e., first-order) transitions. Although the theory has now been superseded by the renormalization group and scaling theory formulations, it remains an exceptionally broad and powerful framework for phase transitions, and the associated concept of the Phase transitions#Order parameters, order parameter as a descriptor of the essential character of the transition has proven transformative. Mean-field formulation (no long-range correlation) Landau was motivated to suggest that the free energy of any system should obey two conditions: *Be analytic in the order parameter and its gradients. *Obey the symmetry of the Hamiltonian mechanics, H ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dimensional Regularization
__NOTOC__ In theoretical physics, dimensional regularization is a method introduced by Juan José Giambiagi and as well as – independently and more comprehensively – by Gerard 't Hooft and Martinus J. G. Veltman for regularizing integrals in the evaluation of Feynman diagrams; in other words, assigning values to them that are meromorphic functions of a complex parameter ''d'', the analytic continuation of the number of spacetime dimensions. Dimensional regularization writes a Feynman integral as an integral depending on the spacetime dimension ''d'' and the squared distances (''x''''i''−''x''''j'')2 of the spacetime points ''x''''i'', ... appearing in it. In Euclidean space, the integral often converges for −Re(''d'') sufficiently large, and can be analytically continued from this region to a meromorphic function defined for all complex ''d''. In general, there will be a pole at the physical value (usually 4) of ''d'', which needs to be canceled by renorma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Functional (mathematics)
In mathematics, a functional is a certain type of function. The exact definition of the term varies depending on the subfield (and sometimes even the author). * In linear algebra, it is synonymous with a linear form, which is a linear mapping from a vector space V into its field of scalars (that is, it is an element of the dual space V^*) "Let ''E'' be a free module over a commutative ring ''A''. We view ''A'' as a free module of rank 1 over itself. By the dual module ''E''∨ of ''E'' we shall mean the module Hom(''E'', ''A''). Its elements will be called functionals. Thus a functional on ''E'' is an ''A''-linear map ''f'' : ''E'' → ''A''." * In functional analysis and related fields, it refers to a mapping from a space X into the field of real or complex numbers. "A numerical function ''f''(''x'') defined on a normed linear space ''R'' will be called a ''functional''. A functional ''f''(''x'') is said to be ''linear'' if ''f''(α''x'' + β''y'') = α''f''(''x'') + β ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dimension
In physics and mathematics, the dimension of a mathematical space (or object) is informally defined as the minimum number of coordinates needed to specify any point within it. Thus, a line has a dimension of one (1D) because only one coordinate is needed to specify a point on itfor example, the point at 5 on a number line. A surface, such as the boundary of a cylinder or sphere, has a dimension of two (2D) because two coordinates are needed to specify a point on itfor example, both a latitude and longitude are required to locate a point on the surface of a sphere. A two-dimensional Euclidean space is a two-dimensional space on the plane. The inside of a cube, a cylinder or a sphere is three-dimensional (3D) because three coordinates are needed to locate a point within these spaces. In classical mechanics, space and time are different categories and refer to absolute space and time. That conception of the world is a four-dimensional space but not the one that w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
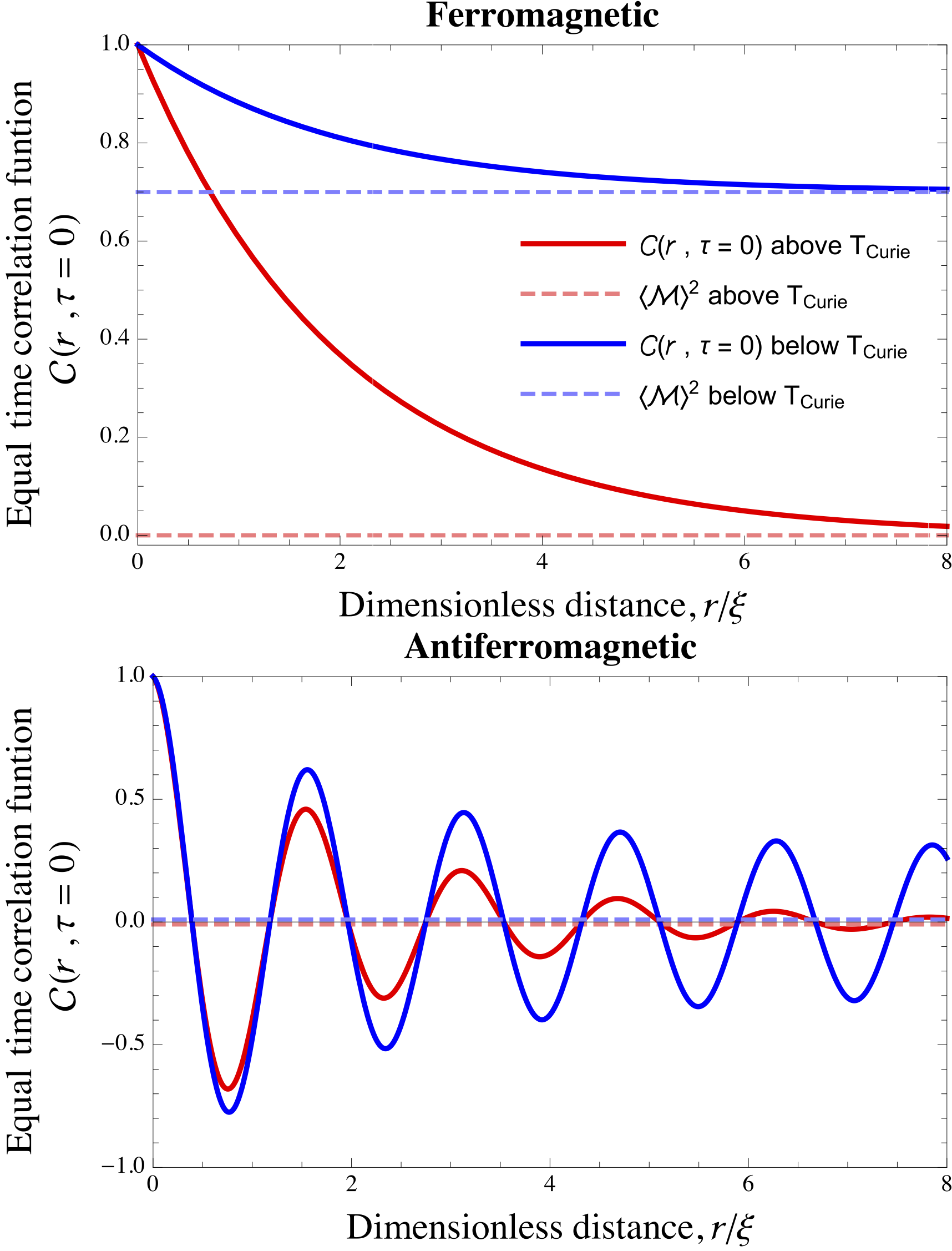
Correlation Function (statistical Mechanics)
In statistical mechanics, the correlation function is a measure of the order in a system, as characterized by a mathematical correlation function. Correlation functions describe how microscopic variables, such as spin and density, at different positions or times are related. More specifically, correlation functions measure quantitatively the extent to which microscopic variables fluctuate together, on average, across space and/or time. Keep in mind that correlation doesn’t automatically equate to causation. So, even if there’s a non-zero correlation between two points in space or time, it doesn’t mean there is a direct causal link between them. Sometimes, a correlation can exist without any causal relationship. This could be purely coincidental or due to other underlying factors, known as confounding variables, which cause both points to covary (statistically). A classic example of spatial correlation can be seen in ferromagnetic and antiferromagnetic materials. In these ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compressibility
In thermodynamics and fluid mechanics, the compressibility (also known as the coefficient of compressibility or, if the temperature is held constant, the isothermal compressibility) is a measure of the instantaneous relative volume change of a fluid or solid as a response to a pressure (or mean stress) change. In its simple form, the compressibility \kappa (denoted in some fields) may be expressed as :\beta =-\frac\frac, where is volume and is pressure. The choice to define compressibility as the negative of the fraction makes compressibility positive in the (usual) case that an increase in pressure induces a reduction in volume. The reciprocal of compressibility at fixed temperature is called the isothermal bulk modulus. Definition The specification above is incomplete, because for any object or system the magnitude of the compressibility depends strongly on whether the process is isentropic or isothermal. Accordingly, isothermal compressibility is defined: :\beta_T=-\ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Response Function
A linear response function describes the input-output relationship of a signal transducer, such as a radio turning electromagnetic waves into music or a neuron turning synaptic input into a response. Because of its many applications in information theory, physics and engineering there exist alternative names for specific linear response functions such as susceptibility, impulse response or impedance; see also transfer function. The concept of a Green's function or fundamental solution of an ordinary differential equation is closely related. Mathematical definition Denote the input of a system by h(t) (e.g. a force), and the response of the system by x(t) (e.g. a position). Generally, the value of x(t) will depend not only on the present value of h(t), but also on past values. Approximately x(t) is a weighted sum of the previous values of h(t'), with the weights given by the linear response function \chi(t-t'): x(t) = \int_^t dt'\, \chi(t-t') h(t') + \cdots\,. The explicit te ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Magnetic Field
A magnetic field (sometimes called B-field) is a physical field that describes the magnetic influence on moving electric charges, electric currents, and magnetic materials. A moving charge in a magnetic field experiences a force perpendicular to its own velocity and to the magnetic field. A permanent magnet's magnetic field pulls on ferromagnetic materials such as iron, and attracts or repels other magnets. In addition, a nonuniform magnetic field exerts minuscule forces on "nonmagnetic" materials by three other magnetic effects: paramagnetism, diamagnetism, and antiferromagnetism, although these forces are usually so small they can only be detected by laboratory equipment. Magnetic fields surround magnetized materials, electric currents, and electric fields varying in time. Since both strength and direction of a magnetic field may vary with location, it is described mathematically by a function (mathematics), function assigning a Euclidean vector, vector to each point of space, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chemical Potential
In thermodynamics, the chemical potential of a Chemical specie, species is the energy that can be absorbed or released due to a change of the particle number of the given species, e.g. in a chemical reaction or phase transition. The chemical potential of a species in a mixture is defined as the rate of change of Thermodynamic free energy, free energy of a thermodynamic system with respect to the change in the number of atoms or molecules of the species that are added to the system. Thus, it is the partial derivative of the free energy with respect to the amount of the species, all other species' concentrations in the mixture remaining constant. When both temperature and pressure are held constant, and the number of particles is expressed in moles, the chemical potential is the partial Molar concentration, molar Gibbs free energy. At chemical equilibrium or in phase equilibrium, the total sum of the product of chemical potentials and stoichiometric coefficients is zero, as the free en ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |