|
Coxeter–Todd Lattice
In mathematics, the Coxeter–Todd lattice K12, discovered by , is a 12-dimensional even integral lattice of discriminant 36 with no norm-2 vectors. It is the sublattice of the Leech lattice fixed by a certain automorphism of order 3, and is analogous to the Barnes–Wall lattice. The automorphism group of the Coxeter–Todd lattice has order 210·37·5·7=78382080, and there are 756 vectors in this lattice of norm 4 (the shortest nonzero vectors in this lattice). Properties The Coxeter–Todd lattice can be made into a 6-dimensional lattice self dual over the Eisenstein integers. The automorphism group of this complex lattice has index 2 in the full automorphism group of the Coxeter–Todd lattice and is a complex reflection group (number 34 on the list) with structure 6.PSU4(F3).2, called the Mitchell group. The genus Genus ( plural genera ) is a taxonomic rank used in the biological classification of extant taxon, living and fossil organisms as well as Virus c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lattice (group)
In geometry and group theory, a lattice in the real coordinate space \mathbb^n is an infinite set of points in this space with the properties that coordinate wise addition or subtraction of two points in the lattice produces another lattice point, that the lattice points are all separated by some minimum distance, and that every point in the space is within some maximum distance of a lattice point. Closure under addition and subtraction means that a lattice must be a subgroup of the additive group of the points in the space, and the requirements of minimum and maximum distance can be summarized by saying that a lattice is a Delone set. More abstractly, a lattice can be described as a free abelian group of dimension n which spans the vector space \mathbb^n. For any basis of \mathbb^n, the subgroup of all linear combinations with integer coefficients of the basis vectors forms a lattice, and every lattice can be formed from a basis in this way. A lattice may be viewed as a regula ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Leech Lattice
In mathematics, the Leech lattice is an even unimodular lattice Λ24 in 24-dimensional Euclidean space, which is one of the best models for the kissing number problem. It was discovered by . It may also have been discovered (but not published) by Ernst Witt in 1940. Characterization The Leech lattice Λ24 is the unique lattice in 24-dimensional Euclidean space, E24, with the following list of properties: *It is unimodular; i.e., it can be generated by the columns of a certain 24×24 matrix with determinant 1. *It is even; i.e., the square of the length of each vector in Λ24 is an even integer. *The length of every non-zero vector in Λ24 is at least 2. The last condition is equivalent to the condition that unit balls centered at the points of Λ24 do not overlap. Each is tangent to 196,560 neighbors, and this is known to be the largest number of non-overlapping 24-dimensional unit balls that can simultaneously touch a single unit ball. This arrangement of 196,560 un ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Barnes–Wall Lattice
In mathematics, the Barnes–Wall lattice Λ16, discovered by Eric Stephen Barnes and G. E. (Tim) Wall (), is the 16-dimensional positive-definite even integral lattice of discriminant 28 with no norm-2 vectors. It is the sublattice of the Leech lattice fixed by a certain automorphism of order 2, and is analogous to the Coxeter–Todd lattice. The automorphism group of the Barnes–Wall lattice has order 89181388800 = 221 35 52 7 and has structure 21+8 PSO8+(F2). There are 4320 vectors of norm 4 in the Barnes–Wall lattice (the shortest nonzero vectors in this lattice). The genus of the Barnes–Wall lattice was described by and contains 24 lattices; all the elements other than the Barnes–Wall lattice have root system of maximal rank 16. The Barnes–Wall lattice is described in detail in . While Λ16 is often referred to as ''the'' Barnes-Wall lattice, their original article in fact construct a family of lattices of increas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
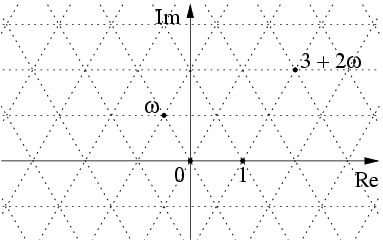
Eisenstein Integers
In mathematics, the Eisenstein integers (named after Gotthold Eisenstein), occasionally also known as Eulerian integers (after Leonhard Euler), are the complex numbers of the form :z = a + b\omega , where and are integers and :\omega = \frac = e^ is a primitive (hence non-real) cube root of unity. The Eisenstein integers form a triangular lattice in the complex plane, in contrast with the Gaussian integers, which form a square lattice in the complex plane. The Eisenstein integers are a countably infinite set. Properties The Eisenstein integers form a commutative ring of algebraic integers in the algebraic number field \mathbb(\omega) — the third cyclotomic field. To see that the Eisenstein integers are algebraic integers note that each is a root of the monic polynomial :z^2 - (2a - b)\;\!z + \left(a^2 - ab + b^2\right)~. In particular, satisfies the equation :\omega^2 + \omega + 1 = 0~. The product of two Eisenstein integers and is given explicitly by :(a + b\;\! ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Reflection Group
In mathematics, a complex reflection group is a finite group acting on a finite-dimensional complex vector space that is generated by complex reflections: non-trivial elements that fix a complex hyperplane pointwise. Complex reflection groups arise in the study of the invariant theory of polynomial rings. In the mid-20th century, they were completely classified in work of Shephard and Todd. Special cases include the symmetric group of permutations, the dihedral groups, and more generally all finite real reflection groups (the Coxeter groups or Weyl groups, including the symmetry groups of regular polyhedra). Definition A (complex) reflection ''r'' (sometimes also called ''pseudo reflection'' or ''unitary reflection'') of a finite-dimensional complex vector space ''V'' is an element r \in GL(V) of finite order that fixes a complex hyperplane pointwise, that is, the ''fixed-space'' \operatorname(r) := \operatorname(r-\operatorname_V) has codimension 1. A (finite) complex reflectio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mitchell Group
Mitchell may refer to: People *Mitchell (surname) *Mitchell (given name) Places Australia * Mitchell, Australian Capital Territory, a light-industrial estate * Mitchell, New South Wales, a suburb of Bathurst * Mitchell, Northern Territory, a suburb of Palmerston * Mitchell, Queensland, a town * Mitchell, South Australia, on lower Eyre Peninsula * Division of Mitchell, a federal Australian Electoral Division in north-west Sydney, New South Wales * Electoral district of Mitchell (Queensland), a former electoral district * Electoral district of Mitchell (South Australia), a state electoral district * Electoral district of Mitchell (Western Australia) a state electoral district * Shire of Mitchell, a local government area in Victoria Canada * Mitchell, Ontario * Mitchell, Manitoba, an unincorporated community * Mitchell Island, British Columbia * Mitchell Island (Nunavut) United Kingdom * Mitchell, Cornwall, a village * Mitchell (UK Parliament constituency) Unite ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Genus Of A Quadratic Form
In mathematics, the genus is a classification of quadratic forms and lattices over the ring of integers. An integral quadratic form is a quadratic form on Z''n'', or equivalently a free Z-module of finite rank. Two such forms are in the same ''genus'' if they are equivalent over the local rings Z''p'' for each prime ''p'' and also equivalent over R. Equivalent forms are in the same genus, but the converse does not hold. For example, ''x''2 + 82''y''2 and 2''x''2 + 41''y''2 are in the same genus but not equivalent over Z. Forms in the same genus have equal discriminant and hence there are only finitely many equivalence classes in a genus. The Smith–Minkowski–Siegel mass formula gives the ''weight'' or ''mass'' of the quadratic forms in a genus, the count of equivalence classes weighted by the reciprocals of the orders of their automorphism groups. Binary quadratic forms For binary quadratic forms there is a group A group is a number of persons or things that are located, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Springer-Verlag
Springer Science+Business Media, commonly known as Springer, is a German multinational publishing company of books, e-books and peer-reviewed journals in science, humanities, technical and medical (STM) publishing. Originally founded in 1842 in Berlin, it expanded internationally in the 1960s, and through mergers in the 1990s and a sale to venture capitalists it fused with Wolters Kluwer and eventually became part of Springer Nature in 2015. Springer has major offices in Berlin, Heidelberg, Dordrecht, and New York City. History Julius Springer founded Springer-Verlag in Berlin in 1842 and his son Ferdinand Springer grew it from a small firm of 4 employees into Germany's then second largest academic publisher with 65 staff in 1872.Chronology ". Springer Science+Business Media. In 1964, Springer expanded its business internationally, o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
