|
Covering Number
In mathematics, a covering number is the number of spherical balls of a given size needed to completely cover a given space, with possible overlaps. Two related concepts are the ''packing number'', the number of disjoint balls that fit in a space, and the ''metric entropy'', the number of points that fit in a space when constrained to lie at some fixed minimum distance apart. Definition Let (''M'', ''d'') be a metric space, let ''K'' be a subset of ''M'', and let ''r'' be a positive real number. Let ''B''''r''(''x'') denote the ball of radius ''r'' centered at ''x''. A subset ''C'' of ''M'' is an ''r-external covering'' of ''K'' if: :K \subseteq \bigcup_ B_r(x). In other words, for every y\in K there exists x\in C such that d(x,y)\leq r. If furthermore ''C'' is a subset of ''K'', then it is an ''r-internal covering''. The external covering number of ''K'', denoted N^_r(K), is the minimum cardinality of any external covering of ''K''. The internal covering number, denoted N^_r( ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Winding Number
In mathematics, the winding number or winding index of a closed curve in the plane around a given point is an integer representing the total number of times that curve travels counterclockwise around the point, i.e., the curve's number of turns. The winding number depends on the orientation of the curve, and it is negative if the curve travels around the point clockwise. Winding numbers are fundamental objects of study in algebraic topology, and they play an important role in vector calculus, complex analysis, geometric topology, differential geometry, and physics (such as in string theory). Intuitive description Suppose we are given a closed, oriented curve in the ''xy'' plane. We can imagine the curve as the path of motion of some object, with the orientation indicating the direction in which the object moves. Then the winding number of the curve is equal to the total number of counterclockwise turns that the object makes around the origin. When counting the total nu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
L-infinity
In mathematics, \ell^\infty, the (real or complex) vector space of bounded sequences with the supremum norm, and L^\infty = L^\infty(X,\Sigma,\mu), the vector space of essentially bounded measurable functions with the essential supremum norm, are two closely related Banach spaces. In fact the former is a special case of the latter. As a Banach space they are the continuous dual of the Banach spaces \ell_1 of absolutely summable sequences, and L^1 = L^1(X,\Sigma, \mu) of absolutely integrable measurable functions (if the measure space fulfills the conditions of being localizable and therefore semifinite). Pointwise multiplication gives them the structure of a Banach algebra, and in fact they are the standard examples of abelian Von Neumann algebras. Sequence space The vector space \ell^\infty is a sequence space whose elements are the bounded sequences. The vector space operations, addition and scalar multiplication, are applied coordinate by coordinate. With respect to the norm ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kissing Number
In geometry, the kissing number of a mathematical space is defined as the greatest number of non-overlapping unit spheres that can be arranged in that space such that they each touch a common unit sphere. For a given sphere packing (arrangement of spheres) in a given space, a kissing number can also be defined for each individual sphere as the number of spheres it touches. For a lattice packing the kissing number is the same for every sphere, but for an arbitrary sphere packing the kissing number may vary from one sphere to another. Other names for kissing number that have been used are Newton number (after the originator of the problem), and contact number. In general, the kissing number problem seeks the maximum possible kissing number for ''n''-dimensional spheres in (''n'' + 1)-dimensional Euclidean space. Ordinary spheres correspond to two-dimensional closed surfaces in three-dimensional space. Finding the kissing number when centers of spheres are confined to a line (the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polygon Covering
In geometry, a covering of a polygon is a set of primitive units (e.g. squares) whose union equals the polygon. A polygon covering problem is a problem of finding a covering with a smallest number of units for a given polygon. This is an important class of problems in computational geometry. There are many different polygon covering problems, depending on the type of polygon being covered. An example polygon covering problem is: given a rectilinear polygon, find a smallest set of squares whose union equals the polygon. In some scenarios, it is not required to cover the entire polygon but only its edges (this is called ''polygon edge covering'') or its vertices (this is called ''polygon vertex covering''). In a covering problem, the units in the covering are allowed to overlap, as long as their union is exactly equal to the target polygon. This is in contrast to a packing problem, in which the units must be disjoint and their union may be smaller than the target polygon, and to a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
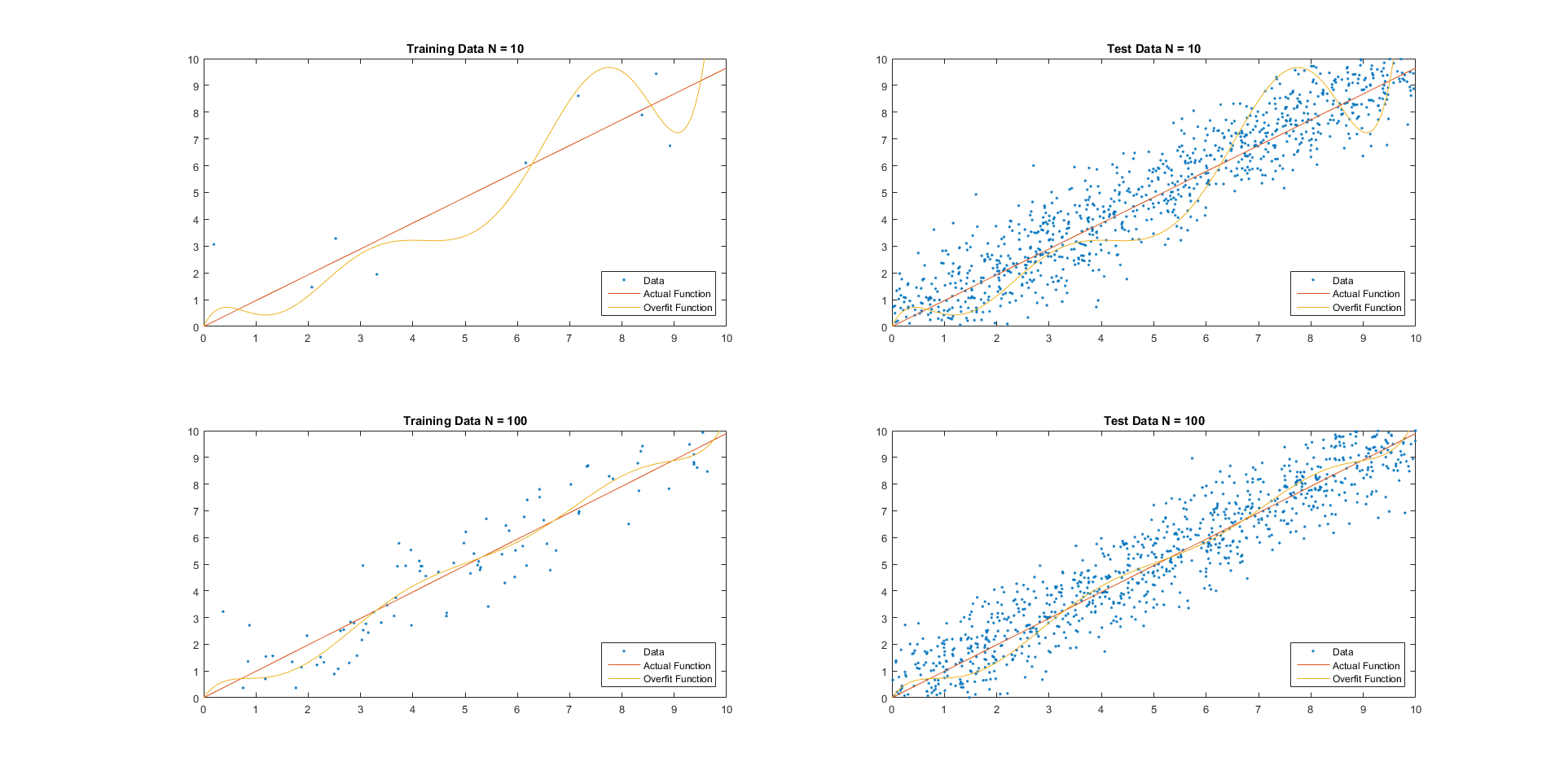
Generalization Error
For supervised learning applications in machine learning and statistical learning theory, generalization error (also known as the out-of-sample error or the risk) is a measure of how accurately an algorithm is able to predict outcome values for previously unseen data. Because learning algorithms are evaluated on finite samples, the evaluation of a learning algorithm may be sensitive to sampling error. As a result, measurements of prediction error on the current data may not provide much information about predictive ability on new data. Generalization error can be minimized by avoiding overfitting in the learning algorithm. The performance of a machine learning algorithm is visualized by plots that show values of ''estimates'' of the generalization error through the learning process, which are called learning curves. Definition In a learning problem, the goal is to develop a function f_n(\vec) that predicts output values y for each input datum \vec. The subscript n indicates tha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lipschitz Constant
In mathematical analysis, Lipschitz continuity, named after German mathematician Rudolf Lipschitz, is a strong form of uniform continuity for functions. Intuitively, a Lipschitz continuous function is limited in how fast it can change: there exists a real number such that, for every pair of points on the graph of this function, the absolute value of the slope of the line connecting them is not greater than this real number; the smallest such bound is called the ''Lipschitz constant'' of the function (or '' modulus of uniform continuity''). For instance, every function that has bounded first derivatives is Lipschitz continuous. In the theory of differential equations, Lipschitz continuity is the central condition of the Picard–Lindelöf theorem which guarantees the existence and uniqueness of the solution to an initial value problem. A special type of Lipschitz continuity, called contraction, is used in the Banach fixed-point theorem. We have the following chain of strict inclus ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lipschitz Function
In mathematical analysis, Lipschitz continuity, named after German mathematician Rudolf Lipschitz, is a strong form of uniform continuity for functions. Intuitively, a Lipschitz continuous function is limited in how fast it can change: there exists a real number such that, for every pair of points on the graph of this function, the absolute value of the slope of the line connecting them is not greater than this real number; the smallest such bound is called the ''Lipschitz constant'' of the function (or '' modulus of uniform continuity''). For instance, every function that has bounded first derivatives is Lipschitz continuous. In the theory of differential equations, Lipschitz continuity is the central condition of the Picard–Lindelöf theorem which guarantees the existence and uniqueness of the solution to an initial value problem. A special type of Lipschitz continuity, called contraction, is used in the Banach fixed-point theorem. We have the following chain of strict inclus ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compact Set
In mathematics, specifically general topology, compactness is a property that seeks to generalize the notion of a closed and bounded subset of Euclidean space by making precise the idea of a space having no "punctures" or "missing endpoints", i.e. that the space not exclude any ''limiting values'' of points. For example, the open interval (0,1) would not be compact because it excludes the limiting values of 0 and 1, whereas the closed interval ,1would be compact. Similarly, the space of rational numbers \mathbb is not compact, because it has infinitely many "punctures" corresponding to the irrational numbers, and the space of real numbers \mathbb is not compact either, because it excludes the two limiting values +\infty and -\infty. However, the ''extended'' real number line ''would'' be compact, since it contains both infinities. There are many ways to make this heuristic notion precise. These ways usually agree in a metric space, but may not be equivalent in other topologic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Metric
In mathematics, the Euclidean distance between two points in Euclidean space is the length of a line segment between the two points. It can be calculated from the Cartesian coordinates of the points using the Pythagorean theorem, therefore occasionally being called the Pythagorean distance. These names come from the ancient Greek mathematicians Euclid and Pythagoras, although Euclid did not represent distances as numbers, and the connection from the Pythagorean theorem to distance calculation was not made until the 18th century. The distance between two objects that are not points is usually defined to be the smallest distance among pairs of points from the two objects. Formulas are known for computing distances between different types of objects, such as the distance from a point to a line. In advanced mathematics, the concept of distance has been generalized to abstract metric spaces, and other distances than Euclidean have been studied. In some applications in statistics an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Degree Of A Continuous Mapping
In topology, the degree of a continuous mapping between two compact oriented manifolds of the same dimension is a number that represents the number of times that the domain manifold wraps around the range manifold under the mapping. The degree is always an integer, but may be positive or negative depending on the orientations. The degree of a map was first defined by Brouwer, who showed that the degree is homotopy invariant (invariant among homotopies), and used it to prove the Brouwer fixed point theorem. In modern mathematics, the degree of a map plays an important role in topology and geometry. In physics, the degree of a continuous map (for instance a map from space to some order parameter set) is one example of a topological quantum number. Definitions of the degree From ''S''''n'' to ''S''''n'' The simplest and most important case is the degree of a continuous map from the n-sphere S^n to itself (in the case n=1, this is called the winding number): Let f\colon S^n\t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, that is, in Euclid's Elements, Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are Euclidean spaces of any positive integer dimension (mathematics), dimension, including the three-dimensional space and the ''Euclidean plane'' (dimension two). The qualifier "Euclidean" is used to distinguish Euclidean spaces from other spaces that were later considered in physics and modern mathematics. Ancient History of geometry#Greek geometry, Greek geometers introduced Euclidean space for modeling the physical space. Their work was collected by the Greek mathematics, ancient Greek mathematician Euclid in his ''Elements'', with the great innovation of ''mathematical proof, proving'' all properties of the space as theorems, by starting from a few fundamental properties, called ''postulates'', which either were considered as eviden ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pairwise Disjoint
In mathematics, two sets are said to be disjoint sets if they have no element in common. Equivalently, two disjoint sets are sets whose intersection is the empty set.. For example, and are ''disjoint sets,'' while and are not disjoint. A collection of two or more sets is called disjoint if any two distinct sets of the collection are disjoint. Generalizations This definition of disjoint sets can be extended to a family of sets \left(A_i\right)_: the family is pairwise disjoint, or mutually disjoint if A_i \cap A_j = \varnothing whenever i \neq j. Alternatively, some authors use the term disjoint to refer to this notion as well. For families the notion of pairwise disjoint or mutually disjoint is sometimes defined in a subtly different manner, in that repeated identical members are allowed: the family is pairwise disjoint if A_i \cap A_j = \varnothing whenever A_i \neq A_j (every two ''distinct'' sets in the family are disjoint).. For example, the collection of sets is d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
