|
Coopmans Approximation
The Coopmans approximation is a method for approximating a fractional-order integrator in a continuous process with constant space complexity. The most correct and accurate methods for calculating the fractional integral require a record of all previous history, and therefore would require a linear space complexity solution O(''n''), where ''n'' is the number of samples measured for the complete history. The fractor ( fractional capacitor ) is an analog component useful in control system A control system manages, commands, directs, or regulates the behavior of other devices or systems using control loops. It can range from a single home heating controller using a thermostat controlling a domestic boiler to large industrial c ...s. In order to model the components behavior in a digital simulation, or replace the fractor in a digital controller, a linear solution is generally untenable. In order to reduce the space complexity however, it is necessary to lose information in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fractional-order Integrator
A fractional-order integrator or just simply fractional integrator is an integrator device that calculates the fractional-order integral or derivative (usually called a differintegral) of an input. Differentiation or integration is a real or complex parameter. The fractional integrator is useful in fractional-order control where the history of the system under control is important to the control system output. Overview The differintegral function, :_a \mathbb^q_t \left( f(x) \right) includes the integer order differentiation and integration functions, and allows a continuous range of functions around them. The differintegral parameters are ''a'', ''t'', and ''q''. The parameters ''a'' and ''t'' describe the range over which to compute the result. The differintegral parameter ''q'' may be any real number or complex number. If ''q'' is greater than zero, the differintegral computes a derivative. If ''q'' is less than zero, the differintegral computes an integral. The integer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Space Complexity
The space complexity of an algorithm or a computer program is the amount of memory space required to solve an instance of the computational problem as a function of characteristics of the input. It is the memory required by an algorithm until it executes completely. Similar to time complexity, space complexity is often expressed asymptotically in big O notation, such as O(n), O(n\log n), O(n^\alpha), O(2^n), etc., where is a characteristic of the input influencing space complexity. Space complexity classes Analogously to time complexity classes DTIME(f(n)) and NTIME(f(n)), the complexity classes DSPACE(f(n)) and NSPACE(f(n)) are the sets of languages that are decidable by deterministic (respectively, non-deterministic) Turing machines that use O(f(n)) space. The complexity classes PSPACE and NPSPACE allow f to be any polynomial, analogously to P and NP. That is, :\mathsf = \bigcup_ \mathsf(n^c) and :\mathsf = \bigcup_ \mathsf(n^c) Relationships between classes The s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Control System
A control system manages, commands, directs, or regulates the behavior of other devices or systems using control loops. It can range from a single home heating controller using a thermostat controlling a domestic boiler to large industrial control systems which are used for controlling processes or machines. The control systems are designed via control engineering process. For continuously modulated control, a feedback controller is used to automatically control a process or operation. The control system compares the value or status of the process variable (PV) being controlled with the desired value or setpoint (SP), and applies the difference as a control signal to bring the process variable output of the plant to the same value as the setpoint. For sequential and combinational logic, software logic, such as in a programmable logic controller, is used. Open-loop and closed-loop control There are two common classes of control action: open loop and closed loop. I ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convolution
In mathematics (in particular, functional analysis), convolution is a mathematical operation on two functions ( and ) that produces a third function (f*g) that expresses how the shape of one is modified by the other. The term ''convolution'' refers to both the result function and to the process of computing it. It is defined as the integral of the product of the two functions after one is reflected about the y-axis and shifted. The choice of which function is reflected and shifted before the integral does not change the integral result (see commutativity). The integral is evaluated for all values of shift, producing the convolution function. Some features of convolution are similar to cross-correlation: for real-valued functions, of a continuous or discrete variable, convolution (f*g) differs from cross-correlation (f \star g) only in that either or is reflected about the y-axis in convolution; thus it is a cross-correlation of and , or and . For complex-valued fu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
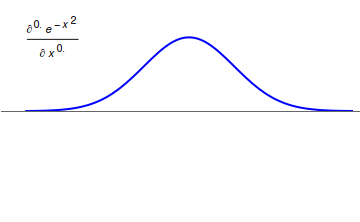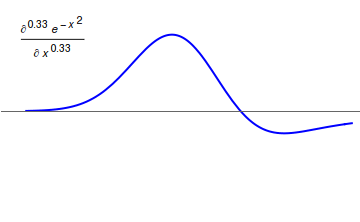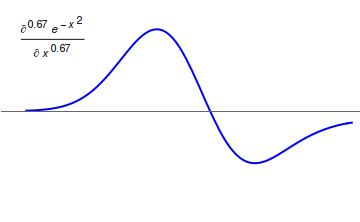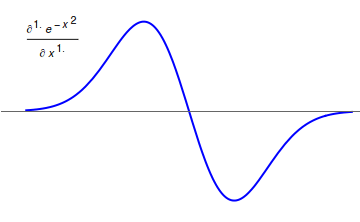
Fractional Calculus
Fractional calculus is a branch of mathematical analysis that studies the several different possibilities of defining real number powers or complex number powers of the differentiation operator D :D f(x) = \frac f(x)\,, and of the integration operator J The symbol J is commonly used instead of the intuitive I in order to avoid confusion with other concepts identified by similar I–like glyphs, such as identities. :J f(x) = \int_0^x f(s) \,ds\,, and developing a calculus for such operators generalizing the classical one. In this context, the term ''powers'' refers to iterative application of a linear operator D to a function f, that is, repeatedly composing D with itself, as in D^n(f) = (\underbrace_n)(f) = \underbrace_n (f)\cdots))). For example, one may ask for a meaningful interpretation of :\sqrt = D^\frac12 as an analogue of the functional square root for the differentiation operator, that is, an expression for some linear operator that, when applied ''twice'' to an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electronic Design
''Electronic Design'' magazine, founded in 1952, is an electronics and electrical engineering trade magazine and website. History Hayden Publishing Company began publishing the bi-weekly magazine Electronic Design in December 1952, and was later published by InformaUSA, Inc. In 1986, Verenigde Nederlandse Uitgeverijen, purchased Hayden Publishing Inc. In June 1988, Verenigde Nederlandse Uitgeverijen, purchased ''Electronic Design'' from McGraw-Hill. In July 1989, Penton Media, purchased ''Electronic Design'', then in Hasbrouck, N.J., from Verenigde Nederlandse Uitgeverijen. In July 2007, Penton Media's OEM electronics publication, ''EE Product News'', merged with Penton Media's "Electronic Design" magazine. ''EE Product News'' was founded in 1941, as a monthly publication. In September 2016, Informa, purchased Penton Media, including ''Electronic Design''. In November 2019, Endeavor Business Media purchased ''Electronic Design'' from Informa. Content Sections i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fractional Calculus
Fractional calculus is a branch of mathematical analysis that studies the several different possibilities of defining real number powers or complex number powers of the differentiation operator D :D f(x) = \frac f(x)\,, and of the integration operator J The symbol J is commonly used instead of the intuitive I in order to avoid confusion with other concepts identified by similar I–like glyphs, such as identities. :J f(x) = \int_0^x f(s) \,ds\,, and developing a calculus for such operators generalizing the classical one. In this context, the term ''powers'' refers to iterative application of a linear operator D to a function f, that is, repeatedly composing D with itself, as in D^n(f) = (\underbrace_n)(f) = \underbrace_n (f)\cdots))). For example, one may ask for a meaningful interpretation of :\sqrt = D^\frac12 as an analogue of the functional square root for the differentiation operator, that is, an expression for some linear operator that, when applied ''twice'' to an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.jpg)