|
Conway Ortho Operator
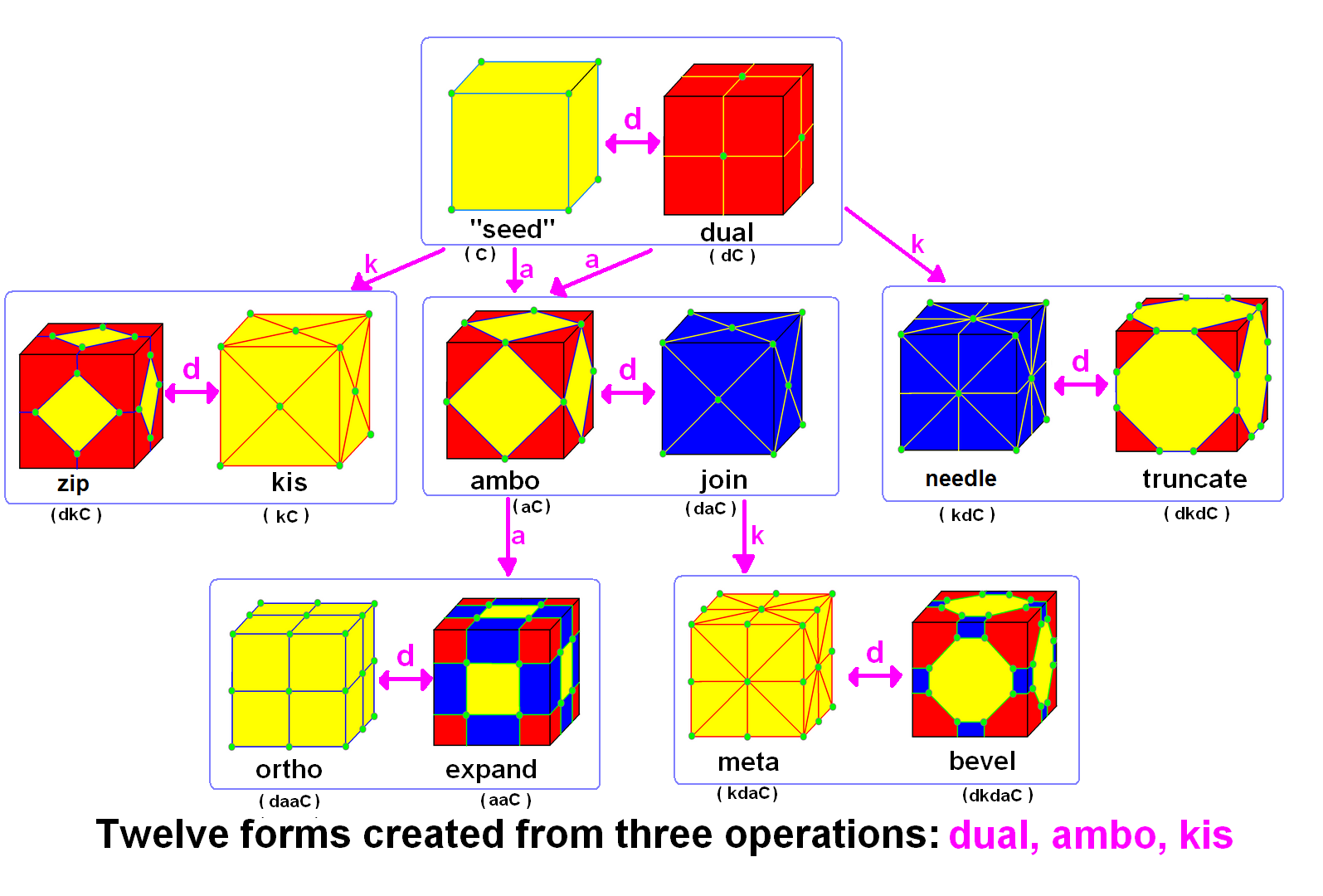
In geometry, Conway polyhedron notation, invented by John Horton Conway and promoted by George W. Hart, is used to describe polyhedra based on a seed polyhedron modified by various prefix operations. Conway and Hart extended the idea of using operators, like truncation as defined by Kepler, to build related polyhedra of the same symmetry. For example, represents a truncated cube, and , parsed as , is (topologically) a truncated cuboctahedron. The simplest operator dual swaps vertex and face elements; e.g., a dual cube is an octahedron: . Applied in a series, these operators allow many higher order polyhedra to be generated. Conway defined the operators (ambo), (bevel), (dual), (expand), (gyro), (join), (kis), (meta), (ortho), ( snub), and ( truncate), while Hart added ( reflect) and (propellor). Later implementations named further operators, sometimes referred to as "extended" operators. Conway's basic operations are sufficient to generate the Archimedean ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conway Relational Chart
Conway may refer to: Places United States * Conway, Arkansas * Conway County, Arkansas * Lake Conway, Arkansas * Conway, Florida * Conway, Iowa * Conway, Kansas * Conway, Louisiana * Conway, Massachusetts * Conway, Michigan * Conway Township, Michigan * Conway, Missouri * Conway, New Hampshire, a New England town ** Conway (CDP), New Hampshire, village in the town * Conway, North Dakota * Conway, North Carolina * Conway, Pennsylvania * Conway, South Carolina * Conway River (Virginia) * Conway, Washington Elsewhere * Conway, Queensland, a locality in the Whitsunday Region, Queensland, Australia * Conway River (New Zealand) * Conway, Wales, now spelt Conwy, a town with a castle in North Wales * River Conway, Wales, similarly respelt River Conwy Ships * HMS ''Conway'' (school ship) * HMS ''Conway'' (1832), a 26-gun sixth rate launched in 1832 * USS ''Conway'' (DD-70) or USS ''Craven'' (DD-70), a Caldwell class destroyer launched in 1918 * USS ''Conway'' (DD-507), ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bevel
A bevelled edge (UK) or beveled edge (US) is an edge of a structure that is not perpendicular to the faces of the piece. The words bevel and chamfer overlap in usage; in general usage they are often interchanged, while in technical usage they may sometimes be differentiated as shown in the image at right. A bevel is typically used to soften the edge of a piece for the sake of safety, wear resistance, or aesthetics; or to facilitate mating with another piece. Applications Cutting tools Most cutting tools have a bevelled edge which is apparent when one examines the grind. Bevel angles can be duplicated using a sliding T bevel. Graphic design Typographic bevels are shading and artificial shadows that emulate the appearance of a 3-dimensional letter. The bevel is a relatively common effect in graphic editors such as Photoshop. As such, it is in widespread use in mainstream logos and other design elements. Glass and mirrors Bevelled edges are a common aesthetic nicety added to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Achiral
Chirality is a property of asymmetry important in several branches of science. The word ''chirality'' is derived from the Greek (''kheir''), "hand", a familiar chiral object. An object or a system is ''chiral'' if it is distinguishable from its mirror image; that is, it cannot be superimposed onto it. Conversely, a mirror image of an ''achiral'' object, such as a sphere, cannot be distinguished from the object. A chiral object and its mirror image are called ''enantiomorphs'' (Greek, "opposite forms") or, when referring to molecules, ''enantiomers''. A non-chiral object is called ''achiral'' (sometimes also ''amphichiral'') and can be superposed on its mirror image. The term was first used by Lord Kelvin in 1893 in the second Robert Boyle Lecture at the Oxford University Junior Scientific Club which was published in 1894: Human hands are perhaps the most recognized example of chirality. The left hand is a non-superimposable mirror image of the right hand; no matter how t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fundamental Domain
Given a topological space and a group acting on it, the images of a single point under the group action form an orbit of the action. A fundamental domain or fundamental region is a subset of the space which contains exactly one point from each of these orbits. It serves as a geometric realization for the abstract set of representatives of the orbits. There are many ways to choose a fundamental domain. Typically, a fundamental domain is required to be a connected subset with some restrictions on its boundary, for example, smooth or polyhedral. The images of a chosen fundamental domain under the group action then tile the space. One general construction of fundamental domains uses Voronoi cells. Hints at a general definition Given an action of a group ''G'' on a topological space ''X'' by homeomorphisms, a fundamental domain for this action is a set ''D'' of representatives for the orbits. It is usually required to be a reasonably nice set topologically, in one of several preci ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Commutative
In mathematics, a binary operation is commutative if changing the order of the operands does not change the result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it. Most familiar as the name of the property that says something like or , the property can also be used in more advanced settings. The name is needed because there are operations, such as division and subtraction, that do not have it (for example, ); such operations are ''not'' commutative, and so are referred to as ''noncommutative operations''. The idea that simple operations, such as the multiplication and addition of numbers, are commutative was for many years implicitly assumed. Thus, this property was not named until the 19th century, when mathematics started to become formalized. A similar property exists for binary relations; a binary relation is said to be symmetric if the relation applies regardless of the order of its operands; for example, equality is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cuboctahedron
A cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such, it is a quasiregular polyhedron, i.e. an Archimedean solid that is not only vertex-transitive but also edge-transitive. It is radially equilateral. Its dual polyhedron is the rhombic dodecahedron. The cuboctahedron was probably known to Plato: Heron's ''Definitiones'' quotes Archimedes as saying that Plato knew of a solid made of 8 triangles and 6 squares. Synonyms *''Vector Equilibrium'' (Buckminster Fuller) because its center-to-vertex radius equals its edge length (it has radial equilateral symmetry). Fuller also called a cuboctahedron built of rigid struts and flexible vertices a ''jitterbug''; this object can be progressively transformed into an icosahedron, octahedron, and tetrahedron by folding along the diagonals of its square sid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Canonical Polyhedron
In geometry, the midsphere or intersphere of a polyhedron is a sphere which is tangent to every edge of the polyhedron. That is to say, it touches any given edge at exactly one point. Not every polyhedron has a midsphere, but for every convex polyhedron there is a combinatorially equivalent polyhedron, the canonical polyhedron, that does have a midsphere. The radius of the midsphere is called the midradius. Examples The uniform polyhedra, including the regular, quasiregular and semiregular polyhedra and their duals all have midspheres. In the regular polyhedra, the inscribed sphere, midsphere, and circumscribed sphere all exist and are concentric, and the midsphere touches each edge at its midpoint. Not every irregular tetrahedron has a midsphere. The tetrahedra that have a midsphere have been called "Crelle's tetrahedra"; they form a four-dimensional subfamily of the six-dimensional space of all tetrahedra (as parameterized by their six edge lengths). Tangent circles If is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Genus (mathematics)
In mathematics, genus (plural genera) has a few different, but closely related, meanings. Intuitively, the genus is the number of "holes" of a surface. A sphere has genus 0, while a torus has genus 1. Topology Orientable surfaces The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It is equal to the number of handles on it. Alternatively, it can be defined in terms of the Euler characteristic ''χ'', via the relationship ''χ'' = 2 − 2''g'' for closed surfaces, where ''g'' is the genus. For surfaces with ''b'' boundary components, the equation reads ''χ'' = 2 − 2''g'' − ''b''. In layman's terms, it's the number of "holes" an object has ("holes" interpreted in the sense of doughnut holes; a hollow sphere would be considered as having zero holes in this sense). A torus has 1 such h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polyhedral Graph
In geometric graph theory, a branch of mathematics, a polyhedral graph is the undirected graph formed from the vertices and edges of a convex polyhedron. Alternatively, in purely graph-theoretic terms, the polyhedral graphs are the 3-vertex-connected, planar graphs. Characterization The Schlegel diagram of a convex polyhedron represents its vertices and edges as points and line segments in the Euclidean plane, forming a subdivision of an outer convex polygon into smaller convex polygons (a convex drawing of the graph of the polyhedron). It has no crossings, so every polyhedral graph is also a planar graph. Additionally, by Balinski's theorem, it is a 3-vertex-connected graph. According to Steinitz's theorem, these two graph-theoretic properties are enough to completely characterize the polyhedral graphs: they are exactly the 3-vertex-connected planar graphs. That is, whenever a graph is both planar and 3-vertex-connected, there exists a polyhedron whose vertices and edges fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graph Embedding
In topological graph theory, an embedding (also spelled imbedding) of a Graph (discrete mathematics), graph G on a surface (mathematics), surface \Sigma is a representation of G on \Sigma in which points of \Sigma are associated with graph theory, vertices and simple arcs (Homeomorphism, homeomorphic images of [0,1]) are associated with graph theory, edges in such a way that: * the endpoints of the arc associated with an edge e are the points associated with the end vertices of e, * no arcs include points associated with other vertices, * two arcs never intersect at a point which is interior to either of the arcs. Here a surface is a compact space, compact, connected space, connected 2-manifold. Informally, an embedding of a graph into a surface is a drawing of the graph on the surface in such a way that its edges may intersect only at their endpoints. It is well known that any finite graph can be embedded in 3-dimensional Euclidean space \mathbb^3.. A planar graph is one that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Platonic Solid
In geometry, a Platonic solid is a convex, regular polyhedron in three-dimensional Euclidean space. Being a regular polyhedron means that the faces are congruent (identical in shape and size) regular polygons (all angles congruent and all edges congruent), and the same number of faces meet at each vertex. There are only five such polyhedra: Geometers have studied the Platonic solids for thousands of years. They are named for the ancient Greek philosopher Plato who hypothesized in one of his dialogues, the ''Timaeus'', that the classical elements were made of these regular solids. History The Platonic solids have been known since antiquity. It has been suggested that certain carved stone balls created by the late Neolithic people of Scotland represent these shapes; however, these balls have rounded knobs rather than being polyhedral, the numbers of knobs frequently differed from the numbers of vertices of the Platonic solids, there is no ball whose knobs match the 20 vertic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Catalan Solid
In mathematics, a Catalan solid, or Archimedean dual, is a dual polyhedron to an Archimedean solid. There are 13 Catalan solids. They are named for the Belgian mathematician Eugène Catalan, who first described them in 1865. The Catalan solids are all convex. They are face-transitive but not vertex-transitive. This is because the dual Archimedean solids are vertex-transitive and not face-transitive. Note that unlike Platonic solids and Archimedean solids, the faces of Catalan solids are ''not'' regular polygons. However, the vertex figures of Catalan solids are regular, and they have constant dihedral angles. Being face-transitive, Catalan solids are isohedron, isohedra. Additionally, two of the Catalan solids are edge-transitive: the rhombic dodecahedron and the rhombic triacontahedron. These are the Quasiregular polyhedron#Quasiregular duals, duals of the two Quasiregular polyhedron, quasi-regular Archimedean solids. Just as Prism (geometry), prisms and antiprisms are ge ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
