|
Convexity Risk
In mathematical finance, convexity refers to non-linearities in a financial model. In other words, if the price of an underlying variable changes, the price of an output does not change linearly, but depends on the second derivative (or, loosely speaking, higher-order terms) of the modeling function. Geometrically, the model is no longer flat but curved, and the degree of curvature is called the convexity. Terminology Strictly speaking, convexity refers to the second derivative of output price with respect to an input price. In derivative pricing, this is referred to as Gamma (Γ), one of the Greeks. In practice the most significant of these is bond convexity, the second derivative of bond price with respect to interest rates. As the second derivative is the first non-linear term, and thus often the most significant, "convexity" is also used loosely to refer to non-linearities generally, including higher-order terms. Refining a model to account for non-linearities is referred t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Finance
Mathematical finance, also known as quantitative finance and financial mathematics, is a field of applied mathematics, concerned with mathematical modeling in the financial field. In general, there exist two separate branches of finance that require advanced quantitative techniques: derivatives pricing on the one hand, and risk and portfolio management on the other. Mathematical finance overlaps heavily with the fields of computational finance and financial engineering. The latter focuses on applications and modeling, often with the help of stochastic asset models, while the former focuses, in addition to analysis, on building tools of implementation for the models. Also related is quantitative investing, which relies on statistical and numerical models (and lately machine learning) as opposed to traditional fundamental analysis when managing portfolios. French mathematician Louis Bachelier's doctoral thesis, defended in 1900, is considered the first scholarly work on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
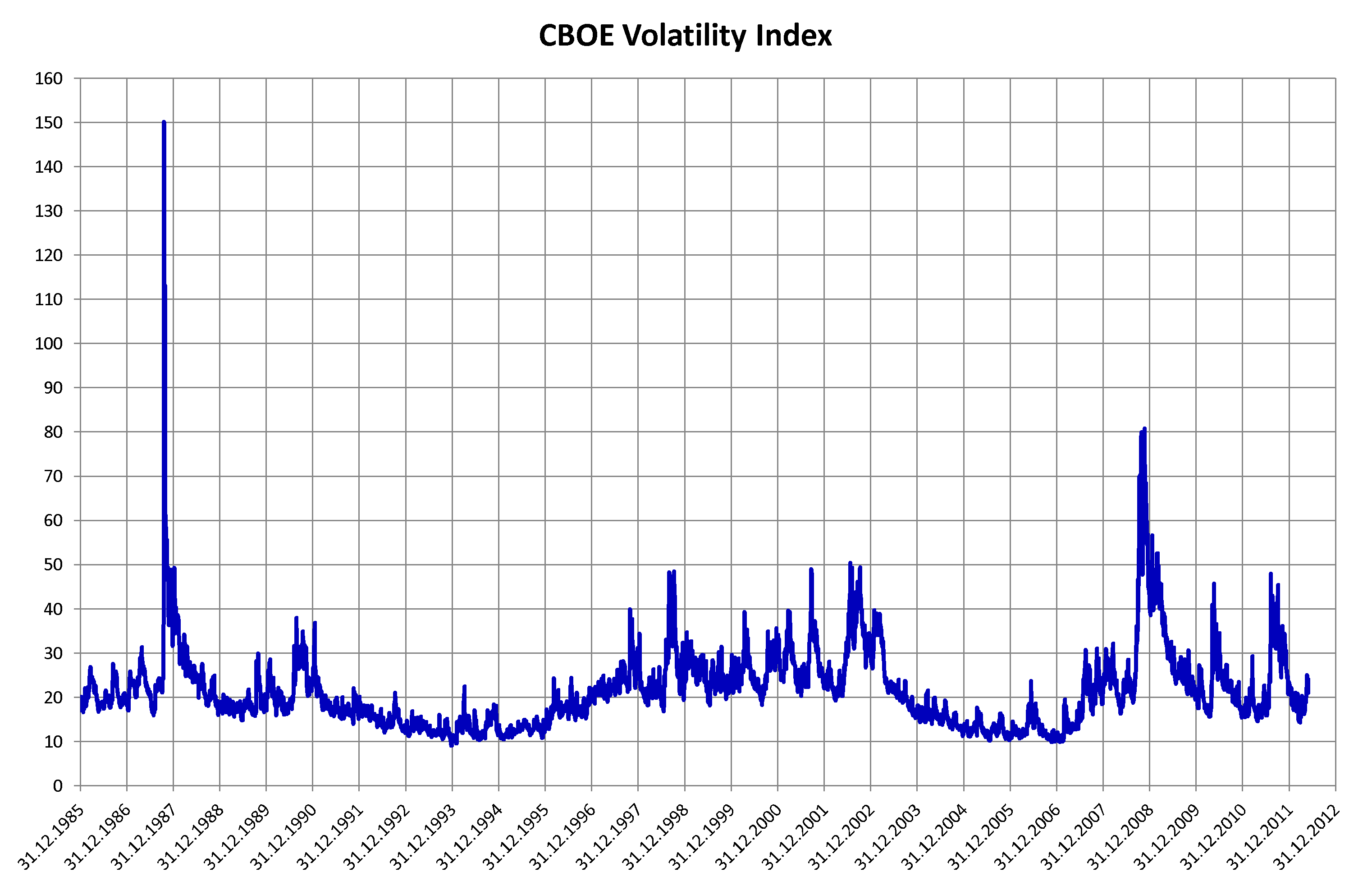
Volatility (finance)
In finance, volatility (usually denoted by "sigma, σ") is the Variability (statistics), degree of variation of a trading price series over time, usually measured by the standard deviation of logarithmic returns. Historic volatility measures a time series of past market prices. Implied volatility looks forward in time, being derived from the market price of a market-traded derivative (in particular, an option). Volatility terminology Volatility as described here refers to the actual volatility, more specifically: * actual current volatility of a financial instrument for a specified period (for example 30 days or 90 days), based on historical prices over the specified period with the last observation the most recent price. * actual historical volatility which refers to the volatility of a financial instrument over a specified period but with the last observation on a date in the past **near synonymous is realized volatility, the square root of the realized variance, in turn c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eurodollar
Eurodollars are U.S. dollars held in time deposit accounts in banks outside the United States. The term was originally applied to U.S. dollar accounts held in banks situated in Europe, but it expanded over the years to cover US dollar accounts held anywhere outside the U.S. Thus, a U.S. dollar-denominated deposit in Dubai or Singapore would likewise be deemed a Eurodollar deposit (sometimes an Asiadollar). More generally, the ''euro-'' prefix can be used to indicate any currency held in a country where it is not the official currency, broadly termed "eurocurrency", for example, Euroyen or even Euroeuro. Eurodollars have different regulatory requirements than dollars held in U.S. banks. Eurodollars can be riskier than assets held in U.S. banks, which include at least partial deposit insurance, and as a result, demand a higher interest rate. There is no connection with the euro currency of the European Union. History After World War II, the quantity of physical U.S. dollar ba ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Callable Bond
A callable bond (also called redeemable bond) is a type of bond ( debt security) that allows the issuer of the bond to retain the privilege of redeeming the bond at some point before the bond reaches its date of maturity. In other words, on the call date(s), the issuer has the right, but not the obligation, to buy back the bonds from the bond holders at a defined call price. Technically speaking, the bonds are not really bought and held by the issuer but are instead cancelled immediately. The call price will usually exceed the par or issue price. In certain cases, mainly in the high-yield debt market, there can be a substantial call premium. Thus, the issuer has an option which it pays for by offering a higher coupon rate. If interest rates in the market have gone down by the time of the call date, the issuer will be able to refinance its debt at a cheaper level and so will be incentivized to call the bonds it originally issued. Another way to look at this interplay is tha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mortgage-backed Securities
A mortgage-backed security (MBS) is a type of asset-backed security (an "Financial instrument, instrument") which is secured by a mortgage loan, mortgage or collection of mortgages. The mortgages are aggregated and sold to a group of individuals (a government agency or investment bank) that securitization, securitizes, or packages, the loans together into a security that investors can buy. Bonds securitizing mortgages are usually treated as a separate class, termed Residential mortgage-backed security, residential; another class is Commercial mortgage-backed security, commercial, depending on whether the underlying asset is mortgages owned by borrowers or assets for commercial purposes ranging from office space to multi-dwelling buildings. The structure of the MBS may be known as pass-through security, "pass-through", where the interest and principal payments from the borrower or homebuyer pass through it to the MBS holder, or it may be more complex, made up of a pool of other MBSs ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Option-adjusted Spread
Option-adjusted spread (OAS) is the yield spread which has to be added to a benchmark yield curve to discount a security's payments to match its market price, using a dynamic pricing model that accounts for embedded options. OAS is hence model-dependent. This concept can be applied to a mortgage-backed security (MBS), or another bond with embedded options, or any other interest rate derivative or option. More loosely, the OAS of a security can be interpreted as its "expected outperformance" versus the benchmarks, if the cash flows and the yield curve behave consistently with the valuation model. In the context of an MBS or callable bond, the embedded option relates primarily to the borrower's right to early repayment, a right commonly exercised via the borrower refinancing the debt. These securities must therefore pay higher yields than noncallable debt, and their values are more fairly compared by OAS than by yield. OAS is usually measured in basis points (bp, or 0.01%) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Constant Maturity Swap
A constant maturity swap (CMS) is a swap that allows the purchaser to fix the duration of received flows on a swap. The floating leg of an interest rate swap typically resets against a published index. The floating leg of a constant maturity swap fixes against a point on the swap curve on a periodic basis. A constant maturity swap is an interest rate swap where the interest rate on one leg is reset periodically, but with reference to a market swap rate rather than LIBOR. The other leg of the swap is generally LIBOR, but may be a fixed rate or potentially another constant maturity rate. Constant maturity swaps can either be single currency or cross currency swaps. Therefore, the prime factor for a constant maturity swap is the shape of the forward implied yield curves. A single currency constant maturity swap versus LIBOR is similar to a series of differential interest rate fixes (or "DIRF") in the same way that an interest rate swap is similar to a series of forward rate agreem ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quanto Options
In finance, the style or family of an option is the class into which the option falls, usually defined by the dates on which the option may be exercised. The vast majority of options are either European or American (style) options. These options—as well as others where the payoff is calculated similarly—are referred to as " vanilla options". Options where the payoff is calculated differently are categorized as "exotic options". Exotic options can pose challenging problems in valuation and hedging. American and European options The key difference between American and European options relates to when the options can be exercised: * A European option may be exercised only at the expiration date of the option, i.e. at a single pre-defined point in time. * An American option on the other hand may be exercised at any time before the expiration date. For both, the payoff—when it occurs—is given by * \max\, for a call option * \max\, for a put option where K is the strike ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Girsanov's Theorem
In probability theory, Girsanov's theorem or the Cameron-Martin-Girsanov theorem explains how stochastic processes change under changes in measure. The theorem is especially important in the theory of financial mathematics as it explains how to convert from the physical measure, which describes the probability that an underlying instrument (such as a share price or interest rate) will take a particular value or values, to the risk-neutral measure which is a very useful tool for evaluating the value of derivatives on the underlying. History Results of this type were first proved by Cameron-Martin in the 1940s and by Igor Girsanov in 1960. They have been subsequently extended to more general classes of process culminating in the general form of Lenglart (1977). Significance Girsanov's theorem is important in the general theory of stochastic processes since it enables the key result that if ''Q'' is a measure that is absolutely continuous with respect to ''P'' then every ''P ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Risk-neutral Measure
In mathematical finance, a risk-neutral measure (also called an equilibrium measure, or '' equivalent martingale measure'') is a probability measure such that each share price is exactly equal to the discounted expectation of the share price under this measure. This is heavily used in the pricing of financial derivatives due to the fundamental theorem of asset pricing, which implies that in a complete market, a derivative's price is the discounted expected value of the future payoff under the unique risk-neutral measure. Such a measure exists if and only if the market is arbitrage-free. A risk-neutral measure is a probability measure The easiest way to remember what the risk-neutral measure is, or to explain it to a probability generalist who might not know much about finance, is to realize that it is: # The probability measure of a transformed random variable. Typically this transformation is the utility function of the payoff. The risk-neutral measure would be the measure co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Martingale (probability Theory)
In probability theory, a martingale is a stochastic process in which the expected value of the next observation, given all prior observations, is equal to the most recent value. In other words, the conditional expectation of the next value, given the past, is equal to the present value. Martingales are used to model fair games, where future expected winnings are equal to the current amount regardless of past outcomes. History Originally, ''martingale (betting system), martingale'' referred to a class of betting strategy, betting strategies that was popular in 18th-century France. The simplest of these strategies was designed for a game in which the gambler wins their stake if a coin comes up heads and loses it if the coin comes up tails. The strategy had the gambler double their bet after every loss so that the first win would recover all previous losses plus win a profit equal to the original stake. As the gambler's wealth and available time jointly approach infinity, their pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Straddle
In finance, a straddle strategy involves two transactions in options on the same underlying, with opposite positions. One holds long risk, the other short. As a result, it involves the purchase or sale of particular option derivatives that allow the holder to profit based on how much the price of the underlying security moves, regardless of the ''direction'' of price movement. A straddle involves buying a call and put with same strike price and expiration date. If the stock price is close to the strike price at expiration of the options, the straddle leads to a loss. However, if there is a sufficiently large move in either direction, a significant profit will result. A straddle is appropriate when an investor is expecting a large move in a stock price but does not know in which direction the move will be. A straddle made from the ''purchase'' of options is known as a long straddle, bottom straddle, or straddle purchase, while the reverse position, made from the ''sale'' of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |