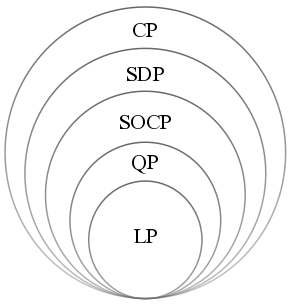
|
Convex Programming
Convex optimization is a subfield of mathematical optimization that studies the problem of minimizing convex functions over convex sets (or, equivalently, maximizing concave functions over convex sets). Many classes of convex optimization problems admit polynomial-time algorithms, whereas mathematical optimization is in general NP-hard. Convex optimization has applications in a wide range of disciplines, such as automatic control systems, estimation and signal processing, communications and networks, electronic circuit design, data analysis and modeling, finance, statistics ( optimal experimental design), and structural optimization, where the approximation concept has proven to be efficient. With recent advancements in computing and optimization algorithms, convex programming is nearly as straightforward as linear programming. Definition A convex optimization problem is an optimization problem in which the objective function is a convex function and the feasible s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Optimization
Mathematical optimization (alternatively spelled ''optimisation'') or mathematical programming is the selection of a best element, with regard to some criterion, from some set of available alternatives. It is generally divided into two subfields: discrete optimization and continuous optimization. Optimization problems of sorts arise in all quantitative disciplines from computer science and engineering to operations research and economics, and the development of solution methods has been of interest in mathematics for centuries. In the more general approach, an optimization problem consists of maxima and minima, maximizing or minimizing a Function of a real variable, real function by systematically choosing Argument of a function, input values from within an allowed set and computing the Value (mathematics), value of the function. The generalization of optimization theory and techniques to other formulations constitutes a large area of applied mathematics. More generally, opti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sublevel Set
In mathematics, a level set of a real-valued function of real variables is a set where the function takes on a given constant value , that is: : L_c(f) = \left\~, When the number of independent variables is two, a level set is called a level curve, also known as ''contour line'' or ''isoline''; so a level curve is the set of all real-valued solutions of an equation in two variables and . When , a level set is called a level surface (or ''isosurface''); so a level surface is the set of all real-valued roots of an equation in three variables , and . For higher values of , the level set is a level hypersurface, the set of all real-valued roots of an equation in variables. A level set is a special case of a fiber. Alternative names Level sets show up in many applications, often under different names. For example, an implicit curve is a level curve, which is considered independently of its neighbor curves, emphasizing that such a curve is defined by an implicit e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conic Optimization
Conic optimization is a subfield of convex optimization that studies problems consisting of minimizing a convex function over the intersection of an affine subspace and a convex cone. The class of conic optimization problems includes some of the most well known classes of convex optimization problems, namely linear and semidefinite programming. Definition Given a real vector space ''X'', a convex, real-valued function :f:C \to \mathbb R defined on a convex cone C \subset X, and an affine subspace \mathcal defined by a set of affine constraints h_i(x) = 0 \ , a conic optimization problem is to find the point x in C \cap \mathcal for which the number f(x) is smallest. Examples of C include the positive orthant \mathbb_+^n = \left\ , positive semidefinite matrices \mathbb^n_, and the second-order cone \left \ . Often f \ is a linear function, in which case the conic optimization problem reduces to a linear program, a semidefinite program, and a second order cone program, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quadratically Constrained Quadratic Programming
In mathematical optimization, a quadratically constrained quadratic program (QCQP) is an optimization problem in which both the objective function and the constraints are quadratic functions. It has the form : \begin & \text && \tfrac12 x^\mathrm P_0 x + q_0^\mathrm x \\ & \text && \tfrac12 x^\mathrm P_i x + q_i^\mathrm x + r_i \leq 0 \quad \text i = 1,\dots,m , \\ &&& Ax = b, \end where ''P''0, …, ''P''''m'' are ''n''-by-''n'' matrices and ''x'' ∈ R''n'' is the optimization variable. If ''P''0, …, ''P''''m'' are all positive semidefinite, then the problem is convex. If these matrices are neither positive nor negative semidefinite, the problem is non-convex. If ''P''1, … ,''P''''m'' are all zero, then the constraints are in fact linear and the problem is a quadratic program. Hardness Solving the general case is an NP-hard problem. To see this, note that the two constraints ''x''1(''x''1 − 1) ≤ 0 and ''x''1(''x''1 − 1) ≥ 0 are equivalen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quadratic Programming
Quadratic programming (QP) is the process of solving certain mathematical optimization problems involving quadratic functions. Specifically, one seeks to optimize (minimize or maximize) a multivariate quadratic function subject to linear constraints on the variables. Quadratic programming is a type of nonlinear programming. "Programming" in this context refers to a formal procedure for solving mathematical problems. This usage dates to the 1940s and is not specifically tied to the more recent notion of "computer programming." To avoid confusion, some practitioners prefer the term "optimization" — e.g., "quadratic optimization." Problem formulation The quadratic programming problem with variables and constraints can be formulated as follows. Given: * a real-valued, -dimensional vector , * an -dimensional real symmetric matrix , * an -dimensional real matrix , and * an -dimensional real vector , the objective of quadratic programming is to find an -dimensional vector , that wi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Programming
Linear programming (LP), also called linear optimization, is a method to achieve the best outcome (such as maximum profit or lowest cost) in a mathematical model whose requirements are represented by linear function#As a polynomial function, linear relationships. Linear programming is a special case of mathematical programming (also known as mathematical optimization). More formally, linear programming is a technique for the mathematical optimization, optimization of a linear objective function, subject to linear equality and linear inequality Constraint (mathematics), constraints. Its feasible region is a convex polytope, which is a set defined as the intersection (mathematics), intersection of finitely many Half-space (geometry), half spaces, each of which is defined by a linear inequality. Its objective function is a real number, real-valued affine function, affine (linear) function defined on this polyhedron. A linear programming algorithm finds a point in the polytope where ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Least Squares
The method of least squares is a standard approach in regression analysis to approximate the solution of overdetermined systems (sets of equations in which there are more equations than unknowns) by minimizing the sum of the squares of the residuals (a residual being the difference between an observed value and the fitted value provided by a model) made in the results of each individual equation. The most important application is in data fitting. When the problem has substantial uncertainties in the independent variable (the ''x'' variable), then simple regression and least-squares methods have problems; in such cases, the methodology required for fitting errors-in-variables models may be considered instead of that for least squares. Least squares problems fall into two categories: linear or ordinary least squares and nonlinear least squares, depending on whether or not the residuals are linear in all unknowns. The linear least-squares problem occurs in statistical regressio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hierarchy Compact Convex
A hierarchy (from Greek: , from , 'president of sacred rites') is an arrangement of items (objects, names, values, categories, etc.) that are represented as being "above", "below", or "at the same level as" one another. Hierarchy is an important concept in a wide variety of fields, such as architecture, philosophy, design, mathematics, computer science, organizational theory, systems theory, systematic biology, and the social sciences (especially political philosophy). A hierarchy can link entities either directly or indirectly, and either vertically or diagonally. The only direct links in a hierarchy, insofar as they are hierarchical, are to one's immediate superior or to one of one's subordinates, although a system that is largely hierarchical can also incorporate alternative hierarchies. Hierarchical links can extend "vertically" upwards or downwards via multiple links in the same direction, following a path. All parts of the hierarchy that are not linked vertically to one ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Farkas' Lemma
Farkas' lemma is a solvability theorem for a finite system of linear inequalities in mathematics. It was originally proven by the Hungarian mathematician Gyula Farkas (natural scientist), Gyula Farkas. Farkas' Lemma (mathematics), lemma is the key result underpinning the linear programming duality and has played a central role in the development of mathematical optimization (alternatively, mathematical programming). It is used amongst other things in the proof of the Karush–Kuhn–Tucker, Karush–Kuhn–Tucker theorem in nonlinear programming. Remarkably, in the area of the foundations of quantum theory, the lemma also underlies the complete set of Bell's theorem, Bell inequalities in the form of necessary and sufficient conditions for the existence of a Local hidden-variable theory, local hidden-variable theory, given data from any specific set of measurements. Generalizations of the Farkas' lemma are about the solvability theorem for convex inequalities, i.e., infinite syste ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Separating Hyperplane Theorem
In geometry, the hyperplane separation theorem is a theorem about disjoint convex sets in ''n''-dimensional Euclidean space. There are several rather similar versions. In one version of the theorem, if both these sets are closed and at least one of them is compact, then there is a hyperplane in between them and even two parallel hyperplanes in between them separated by a gap. In another version, if both disjoint convex sets are open, then there is a hyperplane in between them, but not necessarily any gap. An axis which is orthogonal to a separating hyperplane is a separating axis, because the orthogonal projections of the convex bodies onto the axis are disjoint. The hyperplane separation theorem is due to Hermann Minkowski. The Hahn–Banach separation theorem generalizes the result to topological vector spaces. A related result is the supporting hyperplane theorem. In the context of support-vector machines, the ''optimally separating hyperplane'' or ''maximum-margin hype ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hilbert Projection Theorem
In mathematics, the Hilbert projection theorem is a famous result of convex analysis that says that for every vector x in a Hilbert space H and every nonempty closed convex C \subseteq H, there exists a unique vector m \in C for which \, c - x\, is minimized over the vectors c \in C; that is, such that \, m - x\, \leq \, c - x\, for every c \in C. Finite dimensional case Some intuition for the theorem can be obtained by considering the first order condition In calculus, a derivative test uses the derivatives of a function to locate the critical points of a function and determine whether each point is a local maximum, a local minimum, or a saddle point. Derivative tests can also give information abou ... of the optimization problem. Consider a finite dimensional real Hilbert space H with a subspace C and a point x. If m \in C is a or of the function N : C \to \R defined by N(c) := \, c - x\, (which is the same as the minimum point of c \mapsto \, c - x\, ^2), then deriv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Functional Analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure (e.g. Inner product space#Definition, inner product, Norm (mathematics)#Definition, norm, Topological space#Definition, topology, etc.) and the linear transformation, linear functions defined on these spaces and respecting these structures in a suitable sense. The historical roots of functional analysis lie in the study of function space, spaces of functions and the formulation of properties of transformations of functions such as the Fourier transform as transformations defining continuous function, continuous, unitary operator, unitary etc. operators between function spaces. This point of view turned out to be particularly useful for the study of differential equations, differential and integral equations. The usage of the word ''functional (mathematics), functional'' as a noun goes back to the calculus of variati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
