|
Constructor Theory
Constructor theory is a proposal for a new mode of explanation in fundamental physics in the language of ergodic theory, developed by physicists David Deutsch and Chiara Marletto, at the University of Oxford, since 2012. Constructor theory expresses physical laws exclusively in terms of which physical transformations, or ''tasks'', are possible versus which are impossible, and why. By allowing such counterfactual statements into fundamental physics, it allows new physical laws to be expressed, such as the constructor theory of information. Overview The fundamental elements of the theory are tasks: the abstract specifications of transformations as input–output pairs of attributes. A task is ''impossible'' if there is a law of physics that forbids its being performed with arbitrarily high accuracy, and ''possible'' otherwise. When it is possible, a ''constructor'' for it can be built, again with arbitrary accuracy and reliability. A constructor is an entity that can cause the tas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Physics
Physics is the natural science that studies matter, its fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which relates to the order of nature, or, in other words, to the regular succession of events." Physics is one of the most fundamental scientific disciplines, with its main goal being to understand how the universe behaves. "Physics is one of the most fundamental of the sciences. Scientists of all disciplines use the ideas of physics, including chemists who study the structure of molecules, paleontologists who try to reconstruct how dinosaurs walked, and climatologists who study how human activities affect the atmosphere and oceans. Physics is also the foundation of all engineering and technology. No engineer could design a flat-screen TV, an interplanetary spacecraft, or even a better mousetrap without first understanding the basic laws of physic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Computation
Quantum computing is a type of computation whose operations can harness the phenomena of quantum mechanics, such as superposition, interference, and entanglement. Devices that perform quantum computations are known as quantum computers. Though current quantum computers may be too small to outperform usual (classical) computers for practical applications, larger realizations are believed to be capable of solving certain computational problems, such as integer factorization (which underlies RSA encryption), substantially faster than classical computers. The study of quantum computing is a subfield of quantum information science. There are several models of quantum computation with the most widely used being quantum circuits. Other models include the quantum Turing machine, quantum annealing, and adiabatic quantum computation. Most models are based on the quantum bit, or "qubit", which is somewhat analogous to the bit in classical computation. A qubit can be in a 1 or 0 quantum s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Undecidable Problem
In computability theory and computational complexity theory, an undecidable problem is a decision problem for which it is proved to be impossible to construct an algorithm that always leads to a correct yes-or-no answer. The halting problem is an example: it can be proven that there is no algorithm that correctly determines whether arbitrary programs eventually halt when run. Background A decision problem is any arbitrary yes-or-no question on an infinite set of inputs. Because of this, it is traditional to define the decision problem equivalently as the set of inputs for which the problem returns ''yes''. These inputs can be natural numbers, but also other values of some other kind, such as strings of a formal language. Using some encoding, such as a Gödel numbering, the strings can be encoded as natural numbers. Thus, a decision problem informally phrased in terms of a formal language is also equivalent to a set of natural numbers. To keep the formal definition simple, it is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computability Theory
Computability theory, also known as recursion theory, is a branch of mathematical logic, computer science, and the theory of computation that originated in the 1930s with the study of computable functions and Turing degrees. The field has since expanded to include the study of generalized computability and definability. In these areas, computability theory overlaps with proof theory and effective descriptive set theory. Basic questions addressed by computability theory include: * What does it mean for a function on the natural numbers to be computable? * How can noncomputable functions be classified into a hierarchy based on their level of noncomputability? Although there is considerable overlap in terms of knowledge and methods, mathematical computability theorists study the theory of relative computability, reducibility notions, and degree structures; those in the computer science field focus on the theory of subrecursive hierarchies, formal methods, and formal languages. I ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Calculating Space
''Calculating Space'' (german: Rechnender Raum) is Konrad Zuse's 1969 book on automata theory. He proposed that all processes in the universe are computational. This view is known today as the simulation hypothesis, digital philosophy, digital physics or pancomputationalism. Zuse proposed that the universe is being computed by some sort of cellular automaton or other discrete computing machinery, challenging the long-held view that some physical laws are continuous by nature. He focused on cellular automata as a possible substrate of the computation, and pointed out that the classical notions of entropy and its growth do not make sense in deterministically computed universes. Zuse's thesis was later expanded by German computer scientist Jürgen Schmidhuber in his technical report ''Algorithmic Theories of Everything''. See also * ''A New Kind of Science'' * Simulated reality References Further reading * (70+4 pages) * (98 pages); (69 pages) * External links * Jürgen S ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
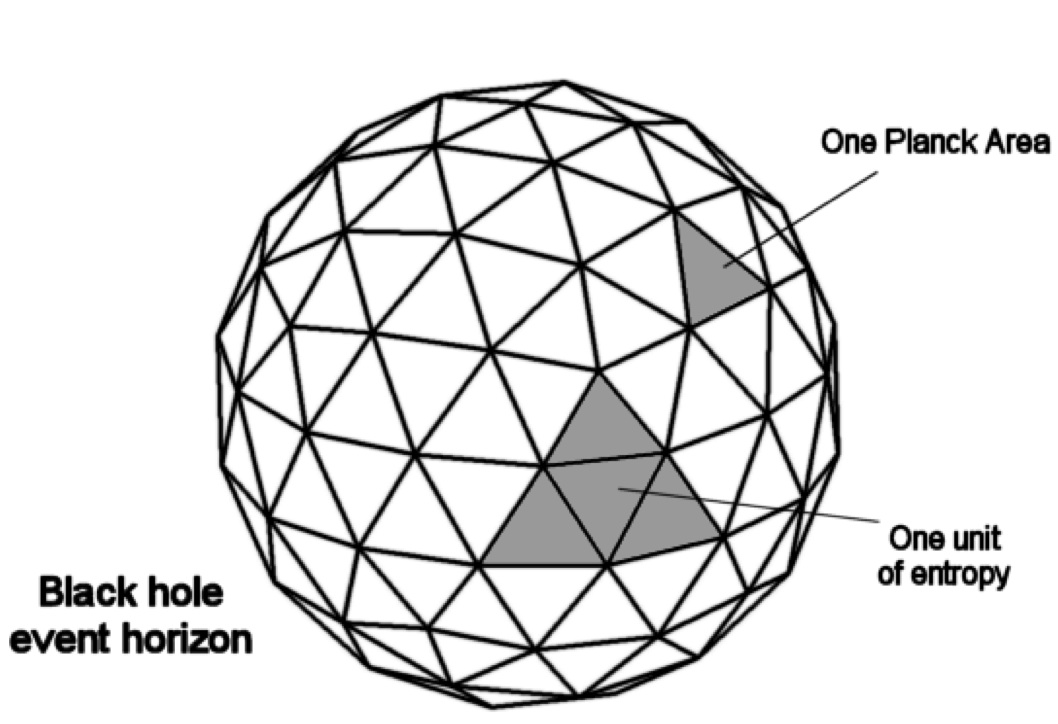
Bekenstein Bound
In physics, the Bekenstein bound (named after Jacob Bekenstein) is an upper limit on the thermodynamic entropy ''S'', or Shannon entropy ''H'', that can be contained within a given finite region of space which has a finite amount of energy—or conversely, the maximal amount of information required to perfectly describe a given physical system down to the quantum level. It implies that the information of a physical system, or the information necessary to perfectly describe that system, must be finite if the region of space and the energy are finite. In computer science this implies that non-finite models such as Turing machines are not realizable as finite devices. Equations The universal form of the bound was originally found by Jacob Bekenstein in 1981 as the inequality : S \leq \frac, where ''S'' is the entropy, ''k'' is the Boltzmann constant, ''R'' is the radius of a sphere that can enclose the given system, ''E'' is the total mass–energy including any rest masses, ''ħ' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Event Horizon
In astrophysics, an event horizon is a boundary beyond which events cannot affect an observer. Wolfgang Rindler coined the term in the 1950s. In 1784, John Michell proposed that gravity can be strong enough in the vicinity of massive compact objects that even light cannot escape. At that time, the Newtonian theory of gravitation and the so-called corpuscular theory of light were dominant. In these theories, if the escape velocity of the gravitational influence of a massive object exceeds the speed of light, then light originating inside or from it can escape temporarily but will return. In 1958, David Finkelstein used general relativity to introduce a stricter definition of a local black hole event horizon as a boundary beyond which events of any kind cannot affect an outside observer, leading to information and firewall paradoxes, encouraging the re-examination of the concept of local event horizons and the notion of black holes. Several theories were subsequently developed, som ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Black Hole
A black hole is a region of spacetime where gravitation, gravity is so strong that nothing, including light or other Electromagnetic radiation, electromagnetic waves, has enough energy to escape it. The theory of general relativity predicts that a sufficiently compact mass can deform spacetime to form a black hole. The boundary (topology), boundary of no escape is called the event horizon. Although it has a great effect on the fate and circumstances of an object crossing it, it has no locally detectable features according to general relativity. In many ways, a black hole acts like an ideal black body, as it reflects no light. Moreover, quantum field theory in curved spacetime predicts that event horizons emit Hawking radiation, with thermal radiation, the same spectrum as a black body of a temperature inversely proportional to its mass. This temperature is of the order of billionths of a kelvin for stellar black holes, making it essentially impossible to observe directly. Obje ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Entropy
Entropy is a scientific concept, as well as a measurable physical property, that is most commonly associated with a state of disorder, randomness, or uncertainty. The term and the concept are used in diverse fields, from classical thermodynamics, where it was first recognized, to the microscopic description of nature in statistical physics, and to the principles of information theory. It has found far-ranging applications in chemistry and physics, in biological systems and their relation to life, in cosmology, economics, sociology, weather science, climate change, and information systems including the transmission of information in telecommunication. The thermodynamic concept was referred to by Scottish scientist and engineer William Rankine in 1850 with the names ''thermodynamic function'' and ''heat-potential''. In 1865, German physicist Rudolf Clausius, one of the leading founders of the field of thermodynamics, defined it as the quotient of an infinitesimal amount of hea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Mechanics
Quantum mechanics is a fundamental theory in physics that provides a description of the physical properties of nature at the scale of atoms and subatomic particles. It is the foundation of all quantum physics including quantum chemistry, quantum field theory, quantum technology, and quantum information science. Classical physics, the collection of theories that existed before the advent of quantum mechanics, describes many aspects of nature at an ordinary (macroscopic) scale, but is not sufficient for describing them at small (atomic and subatomic) scales. Most theories in classical physics can be derived from quantum mechanics as an approximation valid at large (macroscopic) scale. Quantum mechanics differs from classical physics in that energy, momentum, angular momentum, and other quantities of a bound system are restricted to discrete values ( quantization); objects have characteristics of both particles and waves (wave–particle duality); and there are limits to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Information Theory
Information theory is the scientific study of the quantification (science), quantification, computer data storage, storage, and telecommunication, communication of information. The field was originally established by the works of Harry Nyquist and Ralph Hartley, in the 1920s, and Claude Shannon in the 1940s. The field is at the intersection of probability theory, statistics, computer science, statistical mechanics, information engineering (field), information engineering, and electrical engineering. A key measure in information theory is information entropy, entropy. Entropy quantifies the amount of uncertainty involved in the value of a random variable or the outcome of a random process. For example, identifying the outcome of a fair coin flip (with two equally likely outcomes) provides less information (lower entropy) than specifying the outcome from a roll of a dice, die (with six equally likely outcomes). Some other important measures in information theory are mutual informat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.jpg "Click for more on -> Quantum Computation")
