|
Conjunctive Grammar
Conjunctive grammars are a class of formal grammars studied in formal language theory. They extend the basic type of grammars, the context-free grammars, with a conjunction operation. Besides explicit conjunction, conjunctive grammars allow implicit disjunction represented by multiple rules for a single nonterminal symbol, which is the only logical connective expressible in context-free grammars. Conjunction can be used, in particular, to specify intersection of languages. A further extension of conjunctive grammars known as Boolean grammars additionally allows explicit negation. The rules of a conjunctive grammar are of the form :A \to \alpha_1 \And \ldots \And \alpha_m where A is a nonterminal and \alpha_1, ..., \alpha_m are strings formed of symbols in \Sigma and V (finite sets of terminal and nonterminal symbols respectively). Informally, such a rule asserts that every string w over \Sigma that satisfies each of the syntactical conditions represented by \alpha_1, ..., \alpha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Formal Grammar
A formal grammar is a set of Terminal and nonterminal symbols, symbols and the Production (computer science), production rules for rewriting some of them into every possible string of a formal language over an Alphabet (formal languages), alphabet. A grammar does not describe the semantics, meaning of the strings — only their form. In applied mathematics, formal language theory is the discipline that studies formal grammars and languages. Its applications are found in theoretical computer science, theoretical linguistics, Formal semantics (logic), formal semantics, mathematical logic, and other areas. A formal grammar is a Set_(mathematics), set of rules for rewriting strings, along with a "start symbol" from which rewriting starts. Therefore, a grammar is usually thought of as a language generator. However, it can also sometimes be used as the basis for a "recognizer"—a function in computing that determines whether a given string belongs to the language or is grammatical ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
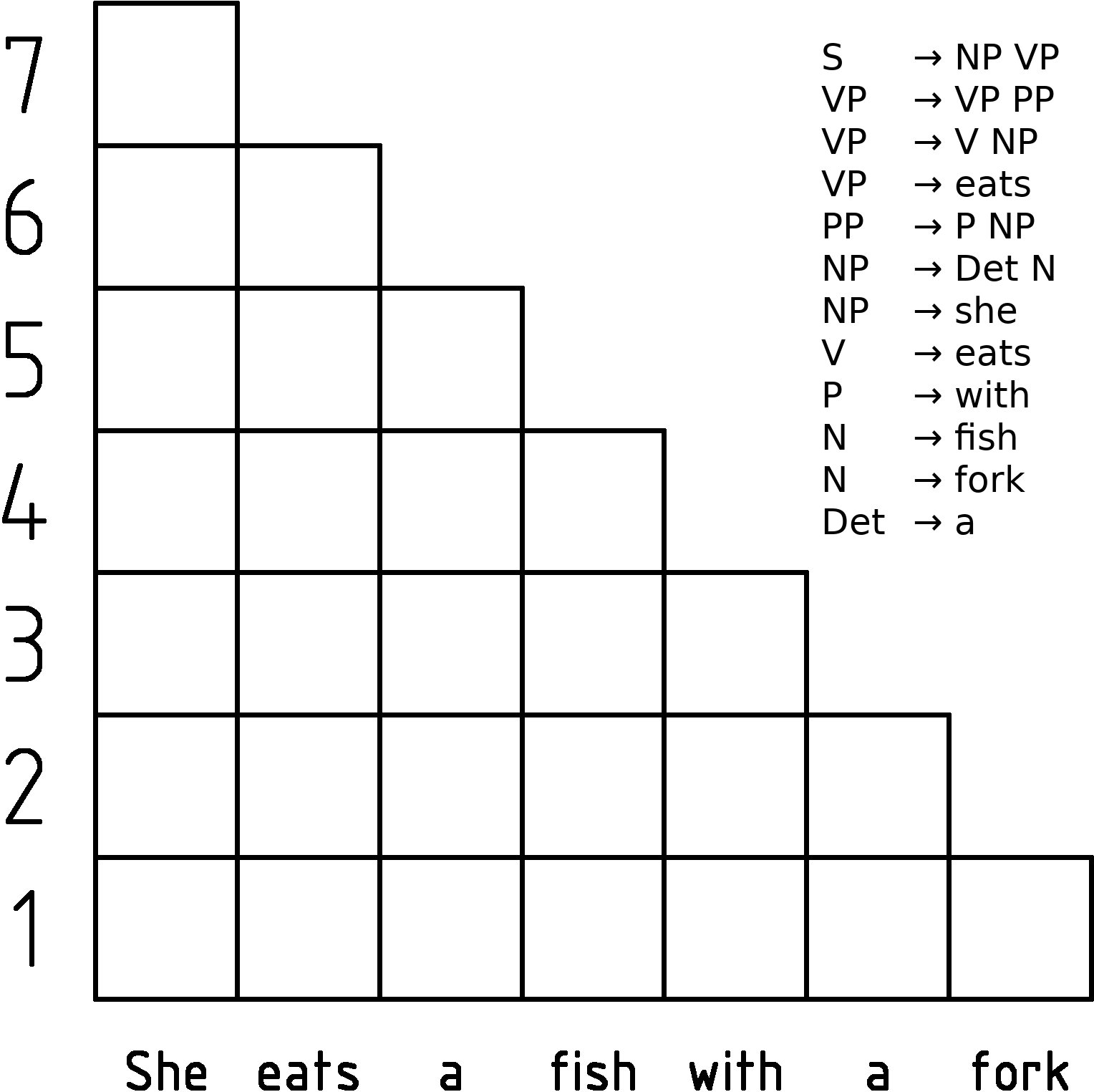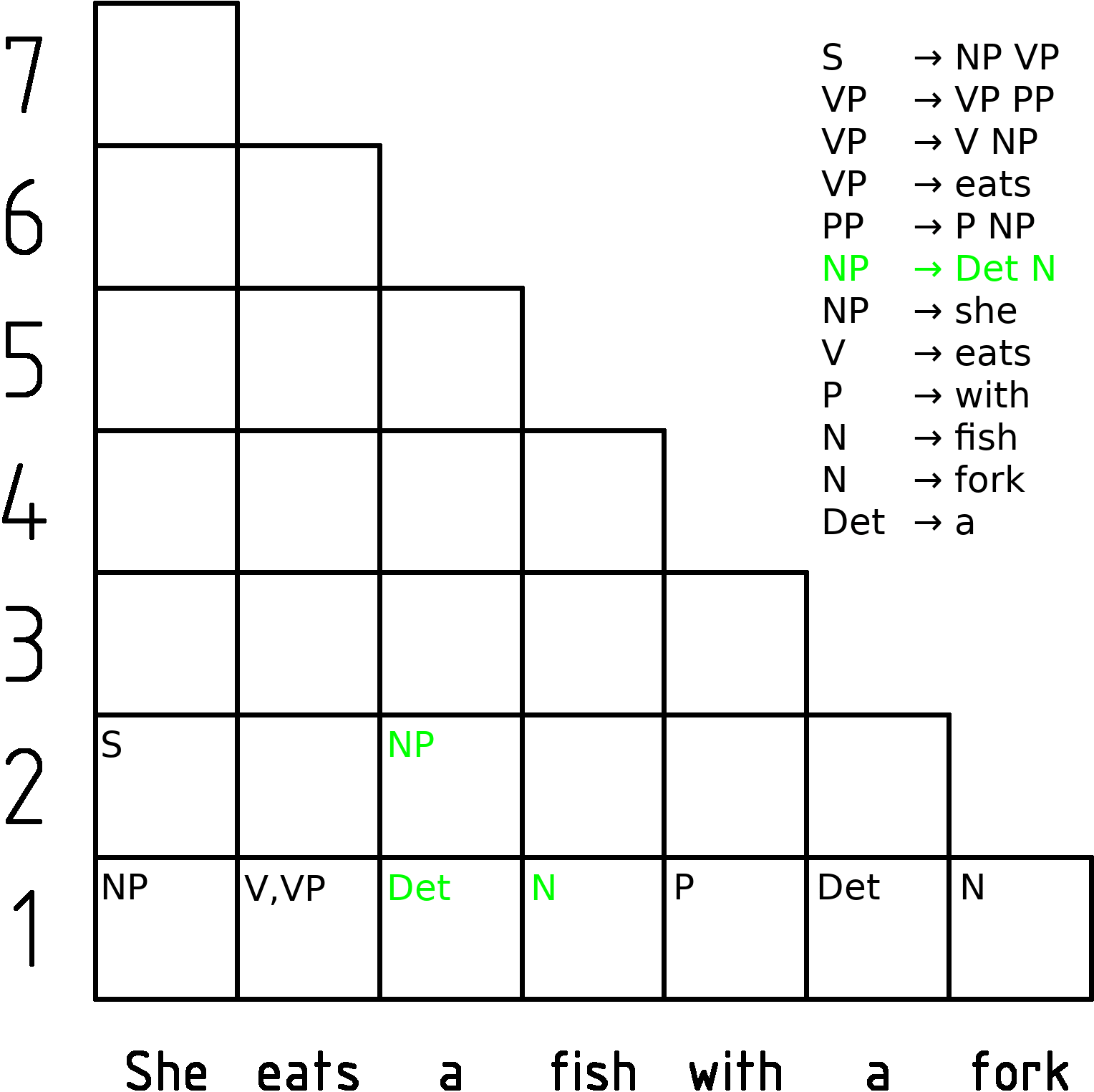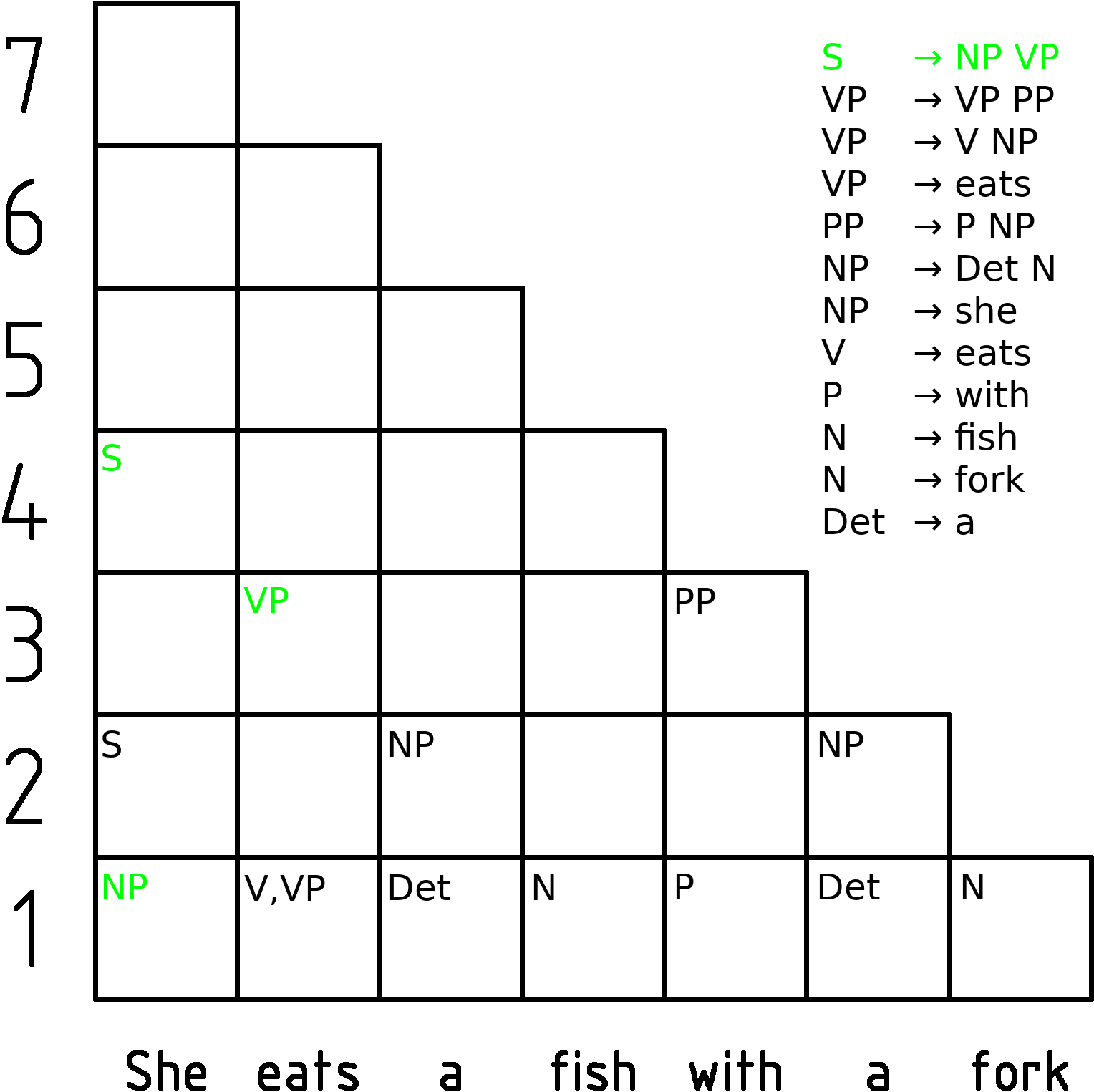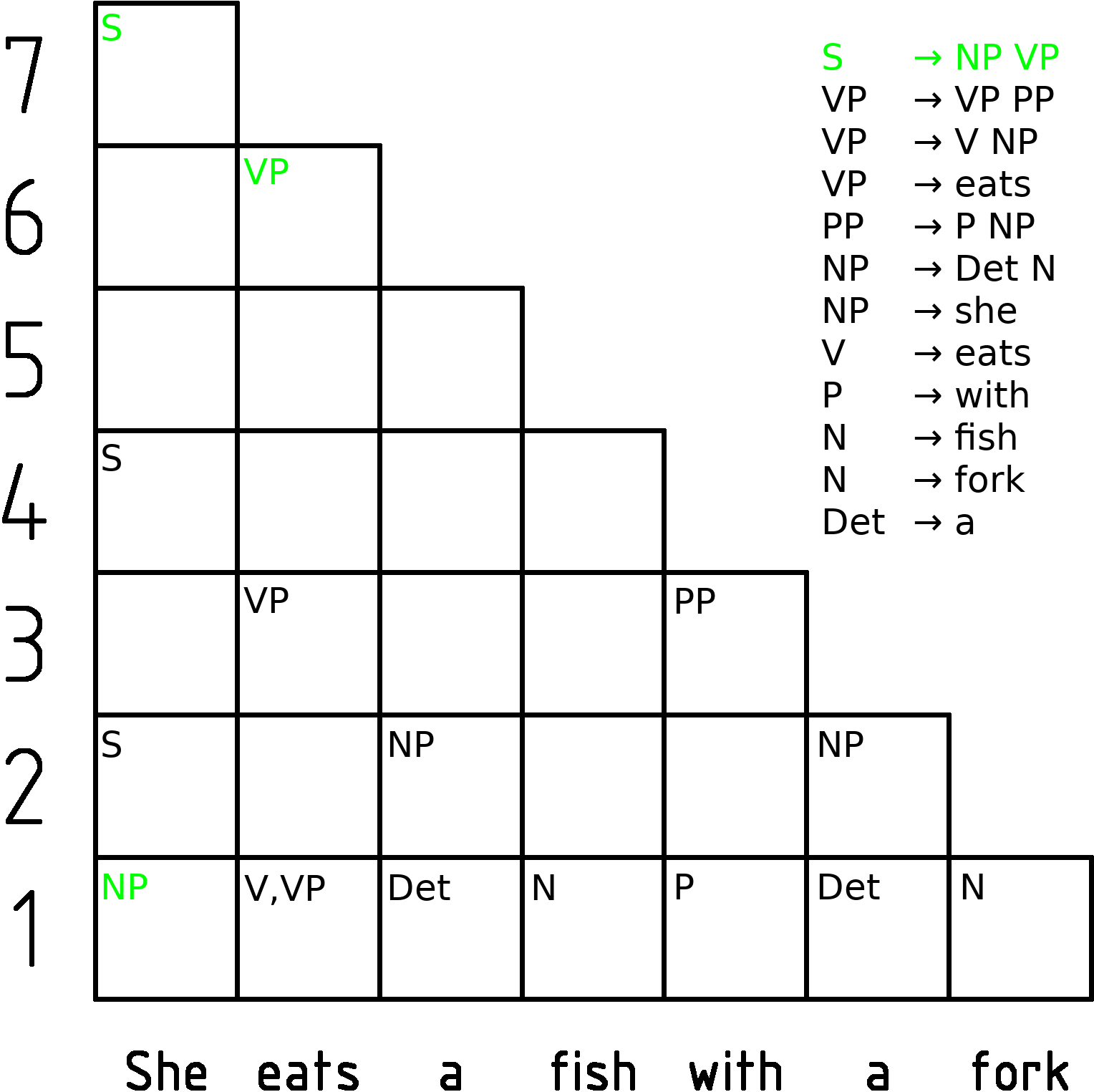
CYK Algorithm
In computer science, the Cocke–Younger–Kasami algorithm (alternatively called CYK, or CKY) is a parsing algorithm for context-free grammars published by Itiroo Sakai in 1961. The algorithm is named after some of its rediscoverers: John Cocke, Daniel Younger, Tadao Kasami, and Jacob T. Schwartz. It employs bottom-up parsing and dynamic programming. The standard version of CYK operates only on context-free grammars given in Chomsky normal form (CNF). However any context-free grammar may be algorithmically transformed into a CNF grammar expressing the same language . The importance of the CYK algorithm stems from its high efficiency in certain situations. Using big ''O'' notation, the worst case running time of CYK is \mathcal\left( n^3 \cdot \left, G \ \right), where n is the length of the parsed string and \left, G \ is the size of the CNF grammar G . This makes it one of the most efficient parsing algorithms in terms of worst-case asymptotic complexity, althoug ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
International Conference On Developments In Language Theory
DLT, the International Conference on Developments in Language Theory is an academic conference in the field of computer science held annually under the auspices of the European Association for Theoretical Computer Science. Like most theoretical computer science conferences its contributions are strongly peer-reviewed; the articles appear in proceedings published in Springer Lecture Notes in Computer Science. Extended versions of selected papers of each year's conference appear in international journals, such as Theoretical Computer Science and International Journal of Foundations of Computer Science. Topics of the conference Typical topics include: * grammars, acceptors and transducers for words, trees and graphs * algebraic theories of automata * algorithmic, combinatorial and algebraic properties of words and languages * variable length codes * symbolic dynamics * cellular automata * polyominoes and multidimensional patterns * decidability questions * image manipulation an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pushdown Automaton
In the theory of computation, a branch of theoretical computer science, a pushdown automaton (PDA) is a type of automaton that employs a stack. Pushdown automata are used in theories about what can be computed by machines. They are more capable than finite-state machines but less capable than Turing machines (see below). Deterministic pushdown automata can recognize all deterministic context-free languages while nondeterministic ones can recognize all context-free languages, with the former often used in parser design. The term "pushdown" refers to the fact that the stack can be regarded as being "pushed down" like a tray dispenser at a cafeteria, since the operations never work on elements other than the top element. A stack automaton, by contrast, does allow access to and operations on deeper elements. Stack automata can recognize a strictly larger set of languages than pushdown automata. A nested stack automaton allows full access, and also allows stacked values to be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Substring
In formal language theory and computer science, a substring is a contiguous sequence of characters within a string. For instance, "''the best of''" is a substring of "''It was the best of times''". In contrast, "''Itwastimes''" is a subsequence of "''It was the best of times''", but not a substring. Prefixes and suffixes are special cases of substrings. A prefix of a string S is a substring of S that occurs at the beginning of S; likewise, a suffix of a string S is a substring that occurs at the end of S. The substrings of the string "''apple''" would be: "''a''", "''ap''", "''app''", "''appl''", "''apple''", "''p''", "''pp''", "''ppl''", "''pple''", "''pl''", "''ple''", "''l''", "''le''" "''e''", "" (note the empty string at the end). Substring A string u is a substring (or factor) of a string t if there exists two strings p and s such that t = pus. In particular, the empty string is a substring of every string. Example: The string u=ana is equal to substrings (and subs ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prefix Closed
In computer science, in the area of formal language theory, frequent use is made of a variety of string functions; however, the notation used is different from that used for computer programming, and some commonly used functions in the theoretical realm are rarely used when programming. This article defines some of these basic terms. Strings and languages A string is a finite sequence of characters. The empty string is denoted by \varepsilon. The concatenation of two string s and t is denoted by s \cdot t, or shorter by s t. Concatenating with the empty string makes no difference: s \cdot \varepsilon = s = \varepsilon \cdot s. Concatenation of strings is associative: s \cdot (t \cdot u) = (s \cdot t) \cdot u. For example, (\langle b \rangle \cdot \langle l \rangle) \cdot (\varepsilon \cdot \langle ah \rangle) = \langle bl \rangle \cdot \langle ah \rangle = \langle blah \rangle. A language is a finite or infinite set of strings. Besides the usual set operations like union, inters ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kleene Star
In mathematical logic and theoretical computer science, the Kleene star (or Kleene operator or Kleene closure) is a unary operation on a Set (mathematics), set to generate a set of all finite-length strings that are composed of zero or more repetitions of members from . It was named after American mathematician Stephen Cole Kleene, who first introduced and widely used it to characterize Automata theory, automata for regular expressions. In mathematics, it is more commonly known as the free monoid construction. Definition Given a set V, define :V^=\ (the set consists only of the empty string), :V^=V, and define recursively the set :V^=\ for each i>0. V^i is called the i-th power of V, it is a shorthand for the Concatenation#Concatenation of sets of strings, concatenation of V by itself i times. That is, ''V^i'' can be understood to be the set of all strings that can be represented as the concatenation of i members from V. The definition of Kleene star on V is : V^*=\bigcup_V^i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Concatenation
In formal language theory and computer programming, string concatenation is the operation of joining character strings end-to-end. For example, the concatenation of "snow" and "ball" is "snowball". In certain formalizations of concatenation theory, also called string theory, string concatenation is a primitive notion. Syntax In many programming languages, string concatenation is a binary infix operator, and in some it is written without an operator. This is implemented in different ways: * Overloading the plus sign + Example from C#: "Hello, " + "World" has the value "Hello, World". * Dedicated operator, such as . in PHP, & in Visual Basic, and , , in SQL. This has the advantage over reusing + that it allows implicit type conversion to string. * string literal concatenation, which means that adjacent strings are concatenated without any operator. Example from C: "Hello, " "World" has the value "Hello, World". In many scientific publications or standards the con ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Context-free Language
In formal language theory, a context-free language (CFL), also called a Chomsky type-2 language, is a language generated by a context-free grammar (CFG). Context-free languages have many applications in programming languages, in particular, most arithmetic expressions are generated by context-free grammars. Background Context-free grammar Different context-free grammars can generate the same context-free language. Intrinsic properties of the language can be distinguished from extrinsic properties of a particular grammar by comparing multiple grammars that describe the language. Automata The set of all context-free languages is identical to the set of languages accepted by pushdown automata, which makes these languages amenable to parsing. Further, for a given CFG, there is a direct way to produce a pushdown automaton for the grammar (and thereby the corresponding language), though going the other way (producing a grammar given an automaton) is not as direct. Examples An e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regular Language
In theoretical computer science and formal language theory, a regular language (also called a rational language) is a formal language that can be defined by a regular expression, in the strict sense in theoretical computer science (as opposed to many modern regular expression engines, which are Regular expression#Patterns for non-regular languages, augmented with features that allow the recognition of non-regular languages). Alternatively, a regular language can be defined as a language recognised by a finite automaton. The equivalence of regular expressions and finite automata is known as Kleene's theorem (after American mathematician Stephen Cole Kleene). In the Chomsky hierarchy, regular languages are the languages generated by regular grammar, Type-3 grammars. Formal definition The collection of regular languages over an Alphabet (formal languages), alphabet Σ is defined recursively as follows: * The empty language ∅ is a regular language. * For each ''a'' ∈ Σ (''a'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |