|
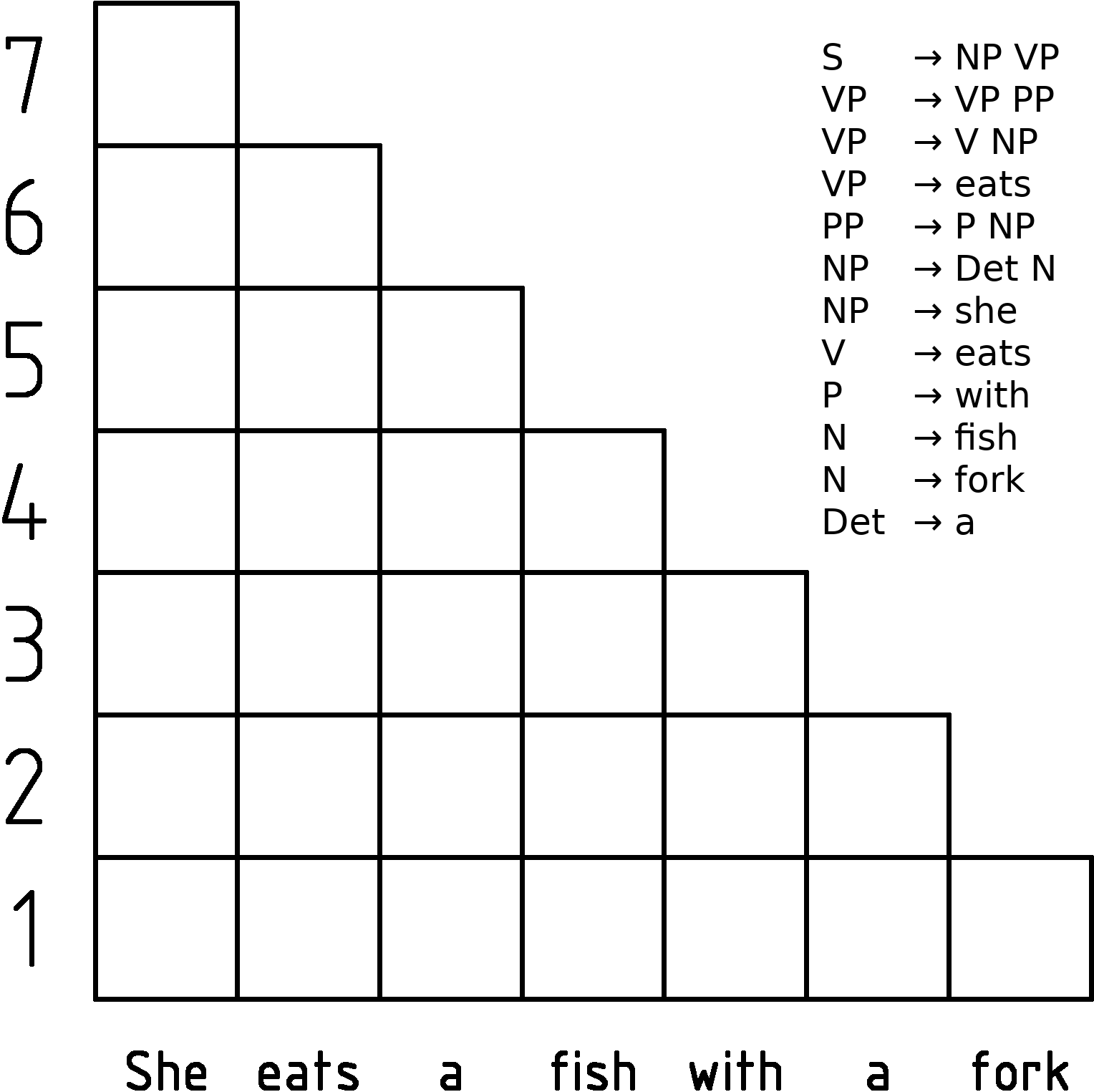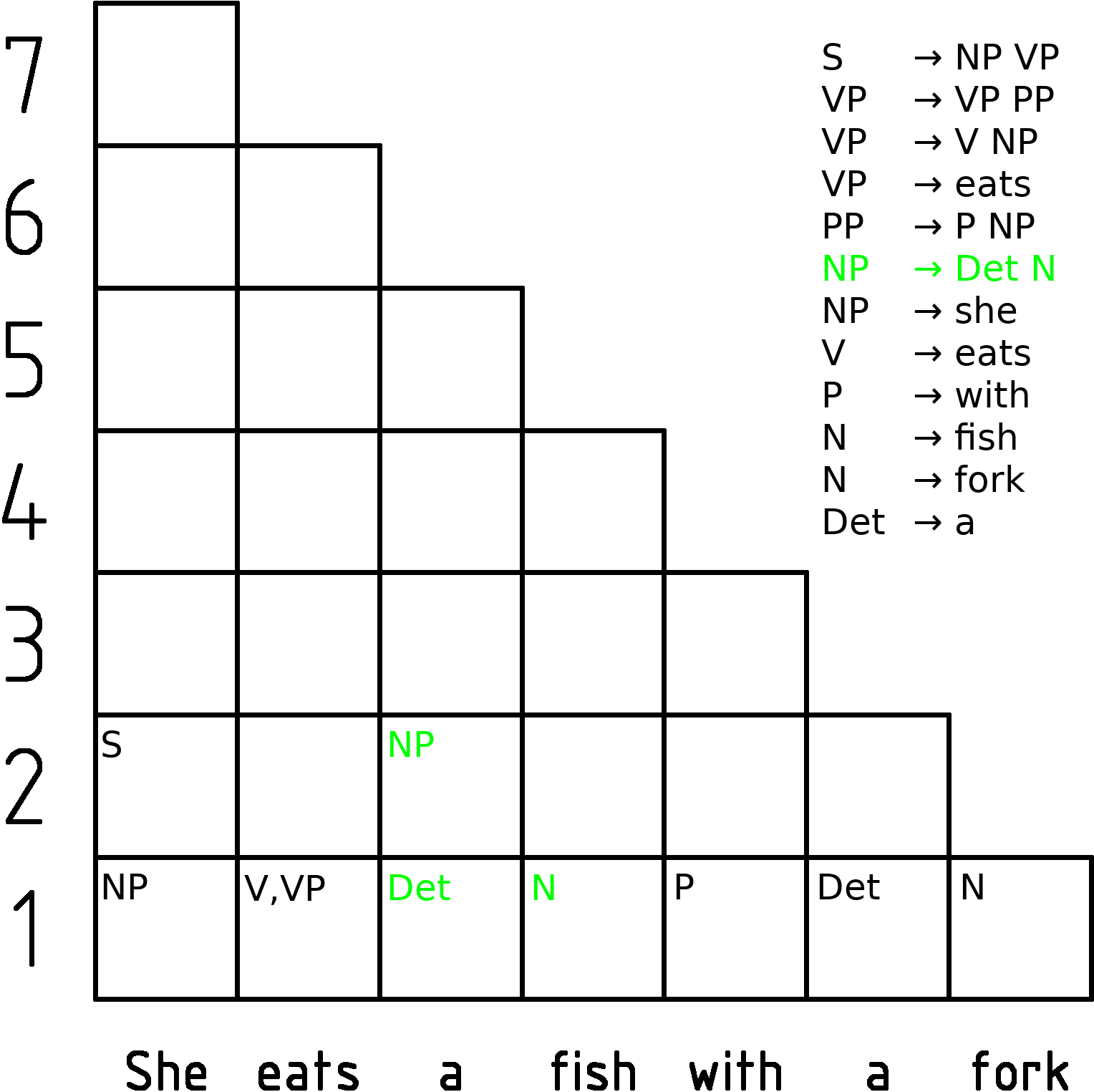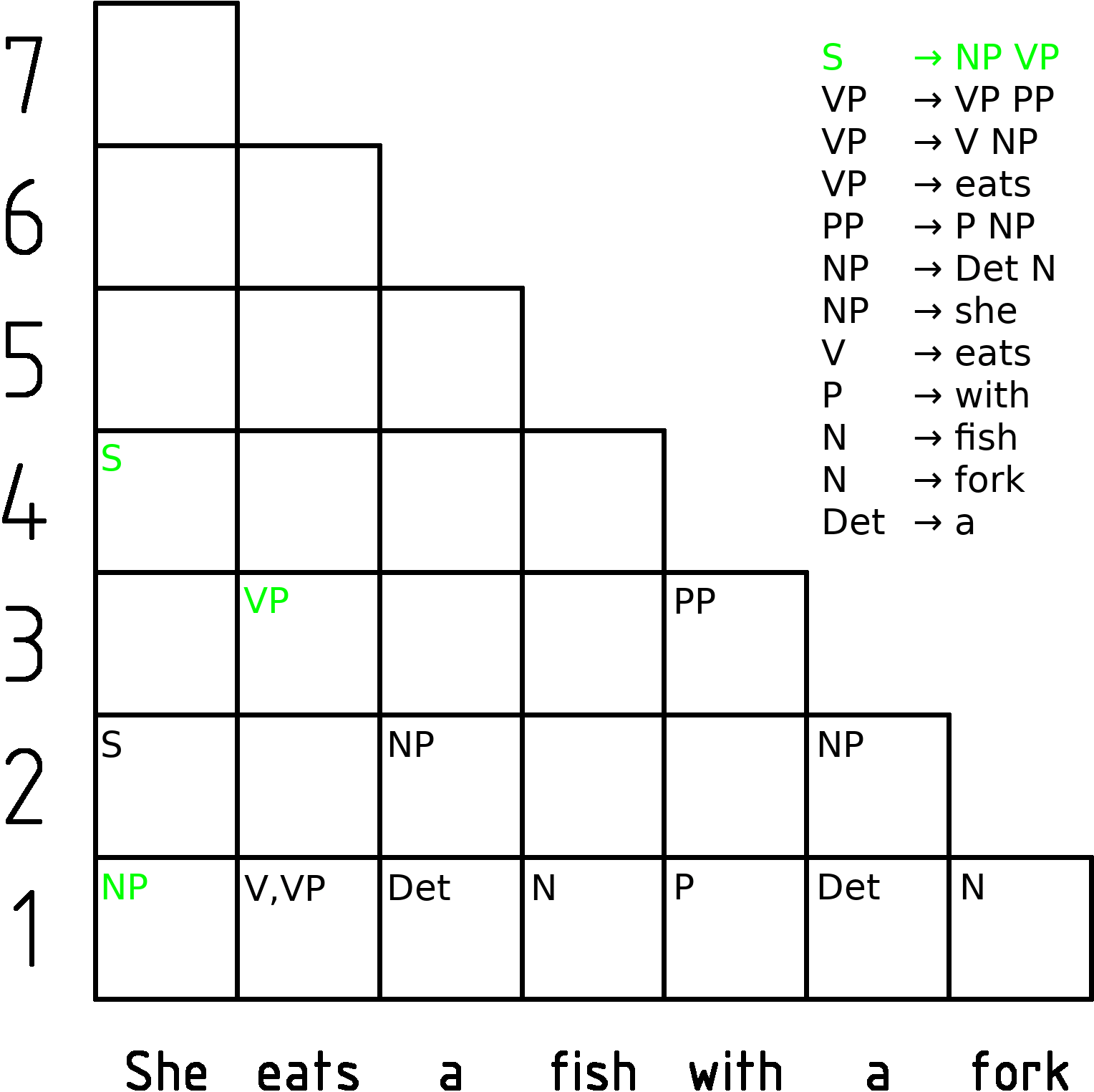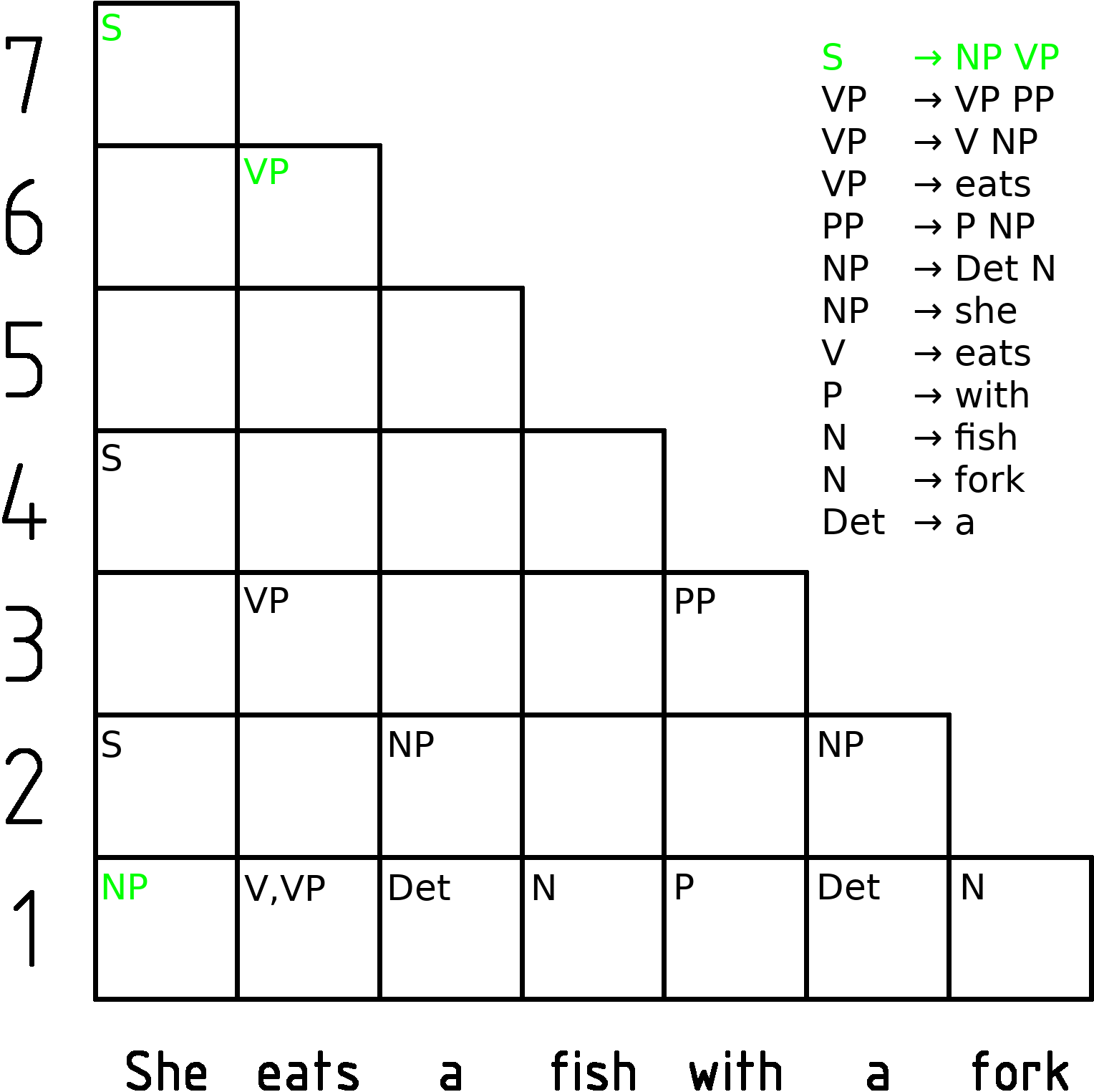
CYK Algorithm
In computer science, the Cocke–Younger–Kasami algorithm (alternatively called CYK, or CKY) is a parsing algorithm for context-free grammars published by Itiroo Sakai in 1961. The algorithm is named after some of its rediscoverers: John Cocke, Daniel Younger, Tadao Kasami, and Jacob T. Schwartz. It employs bottom-up parsing and dynamic programming. The standard version of CYK operates only on context-free grammars given in Chomsky normal form (CNF). However any context-free grammar may be algorithmically transformed into a CNF grammar expressing the same language . The importance of the CYK algorithm stems from its high efficiency in certain situations. Using big ''O'' notation, the worst case running time of CYK is \mathcal\left( n^3 \cdot \left, G \ \right), where n is the length of the parsed string and \left, G \ is the size of the CNF grammar G . This makes it one of the most efficient parsing algorithms in terms of worst-case asymptotic complexity, althoug ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parsing
Parsing, syntax analysis, or syntactic analysis is a process of analyzing a String (computer science), string of Symbol (formal), symbols, either in natural language, computer languages or data structures, conforming to the rules of a formal grammar by breaking it into parts. The term ''parsing'' comes from Latin ''pars'' (''orationis''), meaning Part of speech, part (of speech). The term has slightly different meanings in different branches of linguistics and computer science. Traditional Sentence (linguistics), sentence parsing is often performed as a method of understanding the exact meaning of a sentence or word, sometimes with the aid of devices such as sentence diagrams. It usually emphasizes the importance of grammatical divisions such as subject (grammar), subject and predicate (grammar), predicate. Within computational linguistics the term is used to refer to the formal analysis by a computer of a sentence or other string of words into its constituents, resulting in a par ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
CYK Algorithm Animation Showing Every Step Of A Sentence Parsing
In computer science, the Cocke–Younger–Kasami algorithm (alternatively called CYK, or CKY) is a parsing algorithm for context-free grammars published by Itiroo Sakai in 1961. The algorithm is named after some of its rediscoverers: John Cocke, Daniel Younger, Tadao Kasami, and Jacob T. Schwartz. It employs bottom-up parsing and dynamic programming. The standard version of CYK operates only on context-free grammars given in Chomsky normal form (CNF). However any context-free grammar may be algorithmically transformed into a CNF grammar expressing the same language . The importance of the CYK algorithm stems from its high efficiency in certain situations. Using big ''O'' notation, the worst case running time of CYK is \mathcal\left( n^3 \cdot \left, G \ \right), where n is the length of the parsed string and \left, G \ is the size of the CNF grammar G . This makes it one of the most efficient parsing algorithms in terms of worst-case asymptotic complexity, although ot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Packrat Parser
The Packrat parser is a type of Parsing, parser that shares similarities with the recursive descent parser in its construction. However, it differs because it takes parsing expression grammar, parsing expression grammars (PEGs) as input rather than LL grammar, LL grammars. In 1970, Alexander Birman laid the groundwork for packrat parsing by introducing the "TMG recognition scheme" (TS), and "generalized TS" (gTS). TS was based upon Robert M. McClure's TMG (language), TMG compiler-compiler, and gTS was based upon Dewey Val Schorre's META II, META compiler-compiler. Birman's work was later refined by Aho and Ullman; and renamed as Top-Down Parsing Language (TDPL), and Generalized TDPL (GTDPL), respectively. These algorithms were the first of their kind to employ deterministic top-down parsing with backtracking. Bryan Ford developed PEGs as an expansion of GTDPL and TS. Unlike Context-free grammar, CFGs, PEGs are unambiguous and can match well with machine-oriented languages. PE ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Earley Parser
In computer science, the Earley parser is an algorithm for parsing strings that belong to a given context-free language, though (depending on the variant) it may suffer problems with certain nullable grammars. The algorithm, named after its inventor Jay Earley, is a chart parser that uses dynamic programming; it is mainly used for parsing in computational linguistics. It was first introduced in his dissertation in 1968 (and later appeared in abbreviated, more legible form in a journal). Earley parsers are appealing because they can parse all context-free languages, unlike LR parsers and LL parsers, which are more typically used in compilers but which can only handle restricted classes of languages. The Earley parser executes in cubic time in the general case (n^3), where ''n'' is the length of the parsed string, quadratic time for unambiguous grammars (n^2), and linear time for all deterministic context-free grammars. It performs particularly well when the rules are written l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
GLR Parser
A GLR parser (generalized left-to-right rightmost derivation parser) is an extension of an LR parser algorithm to handle non-deterministic and ambiguous grammars. The theoretical foundation was provided in a 1974 paper by Bernard Lang (along with other general context-free parsers such as GLL). It describes a systematic way to produce such algorithms, and provides uniform results regarding correctness proofs, complexity with respect to grammar classes, and optimization techniques. The first actual implementation of GLR was described in a 1984 paper by Masaru Tomita, it has also been referred to as a "parallel parser". Tomita presented five stages in his original work, though in practice it is the second stage that is recognized as the GLR parser. Though the algorithm has evolved since its original forms, the principles have remained intact. As shown by an earlier publication, Lang was primarily interested in more easily used and more flexible parsers for extensible programming l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Big O Notation
Big ''O'' notation is a mathematical notation that describes the asymptotic analysis, limiting behavior of a function (mathematics), function when the Argument of a function, argument tends towards a particular value or infinity. Big O is a member of a #Related asymptotic notations, family of notations invented by German mathematicians Paul Gustav Heinrich Bachmann, Paul Bachmann, Edmund Landau, and others, collectively called Bachmann–Landau notation or asymptotic notation. The letter O was chosen by Bachmann to stand for '':wikt:Ordnung#German, Ordnung'', meaning the order of approximation. In computer science, big O notation is used to Computational complexity theory, classify algorithms according to how their run time or space requirements grow as the input size grows. In analytic number theory, big O notation is often used to express a bound on the difference between an arithmetic function, arithmetical function and a better understood approximation; one well-known exam ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coppersmith–Winograd Algorithm
Because matrix multiplication is such a central operation in many numerical algorithms, much work has been invested in making matrix multiplication algorithms efficient. Applications of matrix multiplication in computational problems are found in many fields including scientific computing and pattern recognition and in seemingly unrelated problems such as counting the paths through a graph. Many different algorithms have been designed for multiplying matrices on different types of hardware, including parallel and distributed systems, where the computational work is spread over multiple processors (perhaps over a network). Directly applying the mathematical definition of matrix multiplication gives an algorithm that takes time on the order of field operations to multiply two matrices over that field ( in big O notation). Better asymptotic bounds on the time required to multiply matrices have been known since the Strassen's algorithm in the 1960s, but the optimal time (that is, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boolean Matrix
Any kind of logic, function, expression, or theory based on the work of George Boole is considered Boolean. Related to this, "Boolean" may refer to: * Boolean data type, a form of data with only two possible values (usually "true" and "false") * Boolean algebra, a logical calculus of truth values or set membership * Boolean algebra (structure), a set with operations resembling logical ones * Boolean domain, a set consisting of exactly two elements whose interpretations include ''false'' and ''true'' * Boolean circuit, a mathematical model for digital logical circuits. * Boolean expression, an expression in a programming language that produces a Boolean value when evaluated * Boolean function, a function that determines Boolean values or operators * Boolean model (probability theory), a model in stochastic geometry * Boolean network, a certain network consisting of a set of Boolean variables whose state is determined by other variables in the network * Boolean processor, a 1-bit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matrix Multiplication Algorithm
Because matrix multiplication is such a central operation in many numerical algorithms, much work has been invested in making matrix multiplication algorithms efficient. Applications of matrix multiplication in computational problems are found in many fields including scientific computing and pattern recognition and in seemingly unrelated problems such as counting the paths through a Graph (graph theory), graph. Many different algorithms have been designed for multiplying matrices on different types of hardware, including parallel computing, parallel and distributed computing, distributed systems, where the computational work is spread over multiple processors (perhaps over a network). Directly applying the mathematical definition of matrix multiplication gives an algorithm that Analysis of algorithms, takes time on the order of Field (mathematics), field operations to multiply two matrices over that field ( in big O notation). Better asymptotic bounds on the time required to mult ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stochastic Context-free Grammar
In theoretical linguistics and computational linguistics, probabilistic context free grammars (PCFGs) extend context-free grammars, similar to how hidden Markov models extend regular grammars. Each Formal grammar#The syntax of grammars, production is assigned a probability. The probability of a derivation (parse) is the product of the probabilities of the productions used in that derivation. These probabilities can be viewed as parameters of the model, and for large problems it is convenient to learn these parameters via machine learning. A probabilistic grammar's validity is constrained by context of its training dataset. PCFGs originated from grammar theory, and have application in areas as diverse as natural language processing to the study the structure of RNA molecules and design of programming languages. Designing efficient PCFGs has to weigh factors of scalability and generality. Issues such as grammar ambiguity must be resolved. The grammar design affects results accuracy. Gr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Weighted Context-free Grammar
In theoretical linguistics and computational linguistics, probabilistic context free grammars (PCFGs) extend context-free grammars, similar to how hidden Markov models extend regular grammars. Each production is assigned a probability. The probability of a derivation (parse) is the product of the probabilities of the productions used in that derivation. These probabilities can be viewed as parameters of the model, and for large problems it is convenient to learn these parameters via machine learning. A probabilistic grammar's validity is constrained by context of its training dataset. PCFGs originated from grammar theory, and have application in areas as diverse as natural language processing to the study the structure of RNA molecules and design of programming languages. Designing efficient PCFGs has to weigh factors of scalability and generality. Issues such as grammar ambiguity must be resolved. The grammar design affects results accuracy. Grammar parsing algorithms have various ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ambiguous Grammar
In computer science, an ambiguous grammar is a context-free grammar for which there exists a string (computer science), string that can have more than one leftmost derivation or parse tree. Every non-empty context-free language admits an ambiguous grammar by introducing e.g. a duplicate rule. A language that only admits ambiguous grammars is called an #Inherently ambiguous languages, inherently ambiguous language. Deterministic context-free grammars are always unambiguous, and are an important subclass of unambiguous grammars; there are non-deterministic unambiguous grammars, however. For computer programming languages, the reference grammar is often ambiguous, due to issues such as the dangling else problem. If present, these ambiguities are generally resolved by adding precedence rules or other context-sensitive grammar, context-sensitive parsing rules, so the overall phrase grammar is unambiguous. Some parsing algorithms (such as Earley parser, Earley or Generalized LR parser, GL ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |