|
Concatenated Error Correction Code
In coding theory, concatenated codes form a class of error-correcting codes that are derived by combining an inner code and an outer code. They were conceived in 1966 by Dave Forney as a solution to the problem of finding a code that has both exponentially decreasing error probability with increasing block length and polynomial-time decoding complexity. Concatenated codes became widely used in space communications in the 1970s. Background The field of channel coding is concerned with sending a stream of data at the highest possible rate over a given communications channel, and then decoding the original data reliably at the receiver, using encoding and decoding algorithms that are feasible to implement in a given technology. Shannon's channel coding theorem shows that over many common channels there exist channel coding schemes that are able to transmit data reliably at all rates R less than a certain threshold C, called the channel capacity of the given channel. In fact, the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coding Theory
Coding theory is the study of the properties of codes and their respective fitness for specific applications. Codes are used for data compression, cryptography, error detection and correction, data transmission and data storage. Codes are studied by various scientific disciplines—such as information theory, electrical engineering, mathematics, linguistics, and computer science—for the purpose of designing efficient and reliable data transmission methods. This typically involves the removal of redundancy and the correction or detection of errors in the transmitted data. There are four types of coding: # Data compression (or ''source coding'') # Error control (or ''channel coding'') # Cryptographic coding # Line coding Data compression attempts to remove unwanted redundancy from the data from a source in order to transmit it more efficiently. For example, ZIP data compression makes data files smaller, for purposes such as to reduce Internet traffic. Data compression a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Decoding Concatenated Codes
Decoding or decode may refer to: is the process of converting code into plain text or any format that is useful for subsequent processes. Science and technology * Decoding, the reverse of encoding * Parsing, in computer science * Digital-to-analog converter, "decoding" of a digital signal * Phonics, decoding in communication theory * Decode (Oracle) Other uses * deCODE genetics, a biopharmaceutical company based in Iceland * Decode (song), "Decode" (song), a 2008 song by Paramore * Decoding (semiotics), the interpreting of a message communicated to a receiver See also * Code (other) * Decoder (other) * Decoding methods, methods in communication theory for decoding codewords sent over a noisy channel * Codec, a coder-decoder * Recode (other) * Video decoder, an electronic circuit {{disambiguation es:Descodificador ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
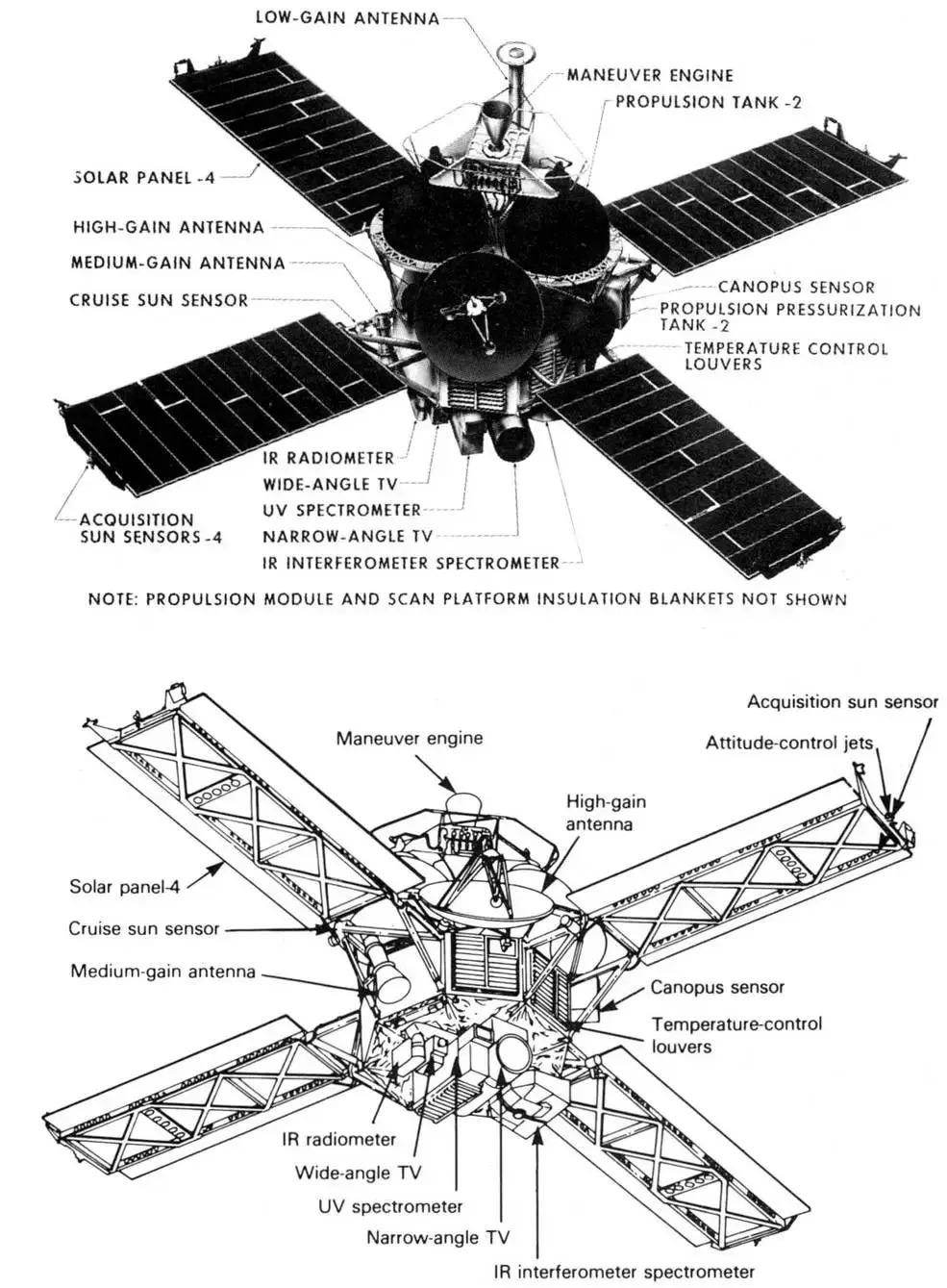
Voyager Program
The Voyager program is an American scientific program that employs two robotic interstellar probes, ''Voyager 1'' and ''Voyager 2''. They were launched in 1977 to take advantage of a favorable alignment of Jupiter and Saturn, to Flyby (spaceflight), fly near them while collecting data for transmission back to Earth. After launch the decision was taken to send ''Voyager 2'' near Uranus and Neptune to collect data for transmission back to Earth. As of 2022, the Voyagers are still in operation past the outer boundary of the heliosphere in interstellar space. They collect and transmit useful data to Earth. , ''Voyager 1'' was moving with a velocity of , or 17 km/s, relative to the Sun, and was from the Sun reaching a distance of from Earth as of February 10, 2022. On 25 August 2012, data from ''Voyager 1'' indicated that it had entered interstellar space. , ''Voyager 2'' was moving with a velocity of , or 15 km/s, relative to the Sun, and was from the Sun reaching a distan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Deep Space Network
The NASA Deep Space Network (DSN) is a worldwide Telecommunications network, network of American spacecraft communication ground segment facilities, located in the United States (California), Spain (Madrid), and Australia (Canberra), that supports National Aeronautics and Space Administration, NASA's interplanetary spaceflight, interplanetary spacecraft missions. It also performs radio astronomy, radio and radar astronomy observations for the exploration of the Solar System and the universe, and supports selected Earth-orbiting missions. DSN is part of the NASA Jet Propulsion Laboratory (JPL). General information DSN currently consists of three deep-space communications facilities placed approximately 120 degrees apart around the Earth. They are: * the Goldstone Deep Space Communications Complex () outside Barstow, California, Barstow, California. For details of Goldstone's contribution to the early days of space probe tracking, see Project Space Track (1957-1961), Project ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mariner 8
Mariner-H (Mariner Mars '71), also commonly known as Mariner 8, was (along with Mariner 9) part of the Mariner Mars '71 project. It was intended to go into Mars orbit and return images and data, but a launch vehicle failure prevented Mariner 8 from achieving Earth orbit and the spacecraft reentered into the Atlantic Ocean shortly after launch. Mission Mariner 8 was launched on an Atlas-Centaur SLV-3C booster (AC-24). The main Centaur engine was ignited 265 seconds after launch, but the upper stage began to oscillate in pitch and tumbled out of control. The Centaur stage shut down 365 seconds after launch due to starvation caused by the tumbling. The Centaur and spacecraft payload separated and re-entered the Earth's atmosphere approximately downrange and fell into the Atlantic Ocean about north of Puerto Rico. A guidance system failure was suspected as the culprit, but JPL navigation chief Bill O'Neil dismissed the idea that the entire guidance system had failed. He argued t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Soft-decision Decoding
In information theory, a soft-decision decoder is a kind of decoding methods – a class of algorithm used to decode data that has been encoded with an error correcting code. Whereas a hard-decision decoder operates on data that take on a fixed set of possible values (typically 0 or 1 in a binary code), the inputs to a soft-decision decoder may take on a whole range of values in-between. This extra information indicates the reliability of each input data point, and is used to form better estimates of the original data. Therefore, a soft-decision decoder will typically perform better in the presence of corrupted data than its hard-decision counterpart. Soft-decision decoders are often used in Viterbi decoders and turbo code decoders. References See also * Forward error correction * Soft-in soft-out decoder A soft-in soft-out (SISO) decoder is a type of soft-decision decoder used with error correcting codes. "Soft-in" refers to the fact that the incoming data may take on v ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Erasure Code
In coding theory, an erasure code is a forward error correction (FEC) code under the assumption of bit erasures (rather than bit errors), which transforms a message of ''k'' symbols into a longer message (code word) with ''n'' symbols such that the original message can be recovered from a subset of the ''n'' symbols. The fraction ''r'' = ''k''/''n'' is called the code rate. The fraction ''k’/k'', where ''k’'' denotes the number of symbols required for recovery, is called reception efficiency. Optimal erasure codes Optimal erasure codes have the property that any ''k'' out of the ''n'' code word symbols are sufficient to recover the original message (i.e., they have optimal reception efficiency). Optimal erasure codes are maximum distance separable codes (MDS codes). Parity check Parity check is the special case where ''n'' = ''k'' + 1. From a set of ''k'' values \_, a checksum is computed and appended to the ''k'' source values: :v_= - \sum_^k v_i. The set of ''k''& ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Generalized Minimum Distance Decoding
In coding theory, generalized minimum-distance (GMD) decoding provides an efficient algorithm for decoding concatenated codes, which is based on using an errors-and- erasures decoder for the outer code. A naive decoding algorithm for concatenated codes can not be an optimal way of decoding because it does not take into account the information that maximum likelihood decoding (MLD) gives. In other words, in the naive algorithm, inner received codewords are treated the same regardless of the difference between their hamming distances. Intuitively, the outer decoder should place higher confidence in symbols whose inner encodings are close to the received word. David Forney in 1966 devised a better algorithm called generalized minimum distance (GMD) decoding which makes use of those information better. This method is achieved by measuring confidence of each received codeword, and erasing symbols whose confidence is below a desired value. And GMD decoding algorithm was one of the first ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Minimum Distance Decoding
In coding theory, decoding is the process of translating received messages into codewords of a given code. There have been many common methods of mapping messages to codewords. These are often used to recover messages sent over a noisy channel, such as a binary symmetric channel. Notation C \subset \mathbb_2^n is considered a binary code with the length n; x,y shall be elements of \mathbb_2^n; and d(x,y) is the distance between those elements. Ideal observer decoding One may be given the message x \in \mathbb_2^n, then ideal observer decoding generates the codeword y \in C. The process results in this solution: :\mathbb(y \mbox \mid x \mbox) For example, a person can choose the codeword y that is most likely to be received as the message x after transmission. Decoding conventions Each codeword does not have an expected possibility: there may be more than one codeword with an equal likelihood of mutating into the received message. In such a case, the sender and receiver(s) must a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Decoding Methods
In coding theory, decoding is the process of translating received messages into codewords of a given code. There have been many common methods of mapping messages to codewords. These are often used to recover messages sent over a noisy channel, such as a binary symmetric channel. Notation C \subset \mathbb_2^n is considered a binary code with the length n; x,y shall be elements of \mathbb_2^n; and d(x,y) is the distance between those elements. Ideal observer decoding One may be given the message x \in \mathbb_2^n, then ideal observer decoding generates the codeword y \in C. The process results in this solution: :\mathbb(y \mbox \mid x \mbox) For example, a person can choose the codeword y that is most likely to be received as the message x after transmission. Decoding conventions Each codeword does not have an expected possibility: there may be more than one codeword with an equal likelihood of mutating into the received message. In such a case, the sender and receiver(s) mus ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exponential Time
In computer science, the time complexity is the computational complexity that describes the amount of computer time it takes to run an algorithm. Time complexity is commonly estimated by counting the number of elementary operations performed by the algorithm, supposing that each elementary operation takes a fixed amount of time to perform. Thus, the amount of time taken and the number of elementary operations performed by the algorithm are taken to be related by a constant factor. Since an algorithm's running time may vary among different inputs of the same size, one commonly considers the worst-case time complexity, which is the maximum amount of time required for inputs of a given size. Less common, and usually specified explicitly, is the average-case complexity, which is the average of the time taken on inputs of a given size (this makes sense because there are only a finite number of possible inputs of a given size). In both cases, the time complexity is generally expresse ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Generator Matrix
In coding theory, a generator matrix is a matrix whose rows form a basis for a linear code. The codewords are all of the linear combinations of the rows of this matrix, that is, the linear code is the row space of its generator matrix. Terminology If G is a matrix, it generates the codewords of a linear code ''C'' by : w=sG where w is a codeword of the linear code ''C'', and s is any input vector. Both w and s are assumed to be row vectors. A generator matrix for a linear , k, dq-code has format k \times n, where ''n'' is the length of a codeword, ''k'' is the number of information bits (the dimension of ''C'' as a vector subspace), ''d'' is the minimum distance of the code, and ''q'' is size of the finite field, that is, the number of symbols in the alphabet (thus, ''q'' = 2 indicates a binary code, etc.). The number of redundant bits is denoted by r = n - k. The ''standard'' form for a generator matrix is, : G = \begin I_k , P \end, where I_k is the k \times k identity ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
