|
Compressed Sensing
Compressed sensing (also known as compressive sensing, compressive sampling, or sparse sampling) is a signal processing technique for efficiently acquiring and reconstructing a Signal (electronics), signal, by finding solutions to Underdetermined system, underdetermined linear systems. This is based on the principle that, through optimization, the sparsity of a signal can be exploited to recover it from far fewer samples than required by the Nyquist–Shannon sampling theorem. There are two conditions under which recovery is possible. The first one is sparsity, which requires the signal to be sparse in some domain. The second one is incoherence, which is applied through the isometric property, which is sufficient for sparse signals. Overview A common goal of the engineering field of signal processing is to reconstruct a signal from a series of sampling measurements. In general, this task is impossible because there is no way to reconstruct a signal during the times that the signa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Signal Processing
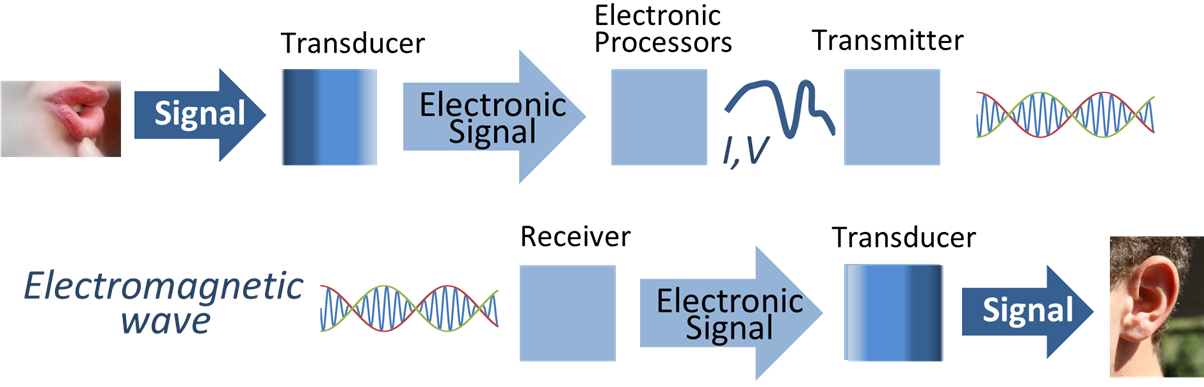
Signal processing is an electrical engineering subfield that focuses on analyzing, modifying and synthesizing ''signals'', such as audio signal processing, sound, image processing, images, and scientific measurements. Signal processing techniques are used to optimize transmissions, Data storage, digital storage efficiency, correcting distorted signals, subjective video quality and to also detect or pinpoint components of interest in a measured signal. History According to Alan V. Oppenheim and Ronald W. Schafer, the principles of signal processing can be found in the classical numerical analysis techniques of the 17th century. They further state that the digital refinement of these techniques can be found in the digital control systems of the 1940s and 1950s. In 1948, Claude Shannon wrote the influential paper "A Mathematical Theory of Communication" which was published in the Bell System Technical Journal. The paper laid the groundwork for later development of information c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
George Dantzig
George Bernard Dantzig (; November 8, 1914 – May 13, 2005) was an American mathematical scientist who made contributions to industrial engineering, operations research, computer science, economics, and statistics. Dantzig is known for his development of the simplex algorithm, an algorithm for solving linear programming problems, and for his other work with linear programming. In statistics, Dantzig solved two open problems in statistical theory, which he had mistaken for homework after arriving late to a lecture by Jerzy Neyman.Joe Holley (2005)"Obituaries of George Dantzig" In: ''Washington Post'', May 19, 2005; B06 At his death, Dantzig was the Professor Emeritus of Transportation Sciences and Professor of Operations Research and of Computer Science at Stanford University. Early life Born in Portland, Oregon, George Bernard Dantzig was named after George Bernard Shaw, the Irish writer.Richard W. Cottle, B. Curtis Eaves and Michael A. Saunders (2006)"Memorial Resolution: Ge ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Underdetermined Equation System
Indeterminacy or underdeterminacy may refer to: Law * Indeterminacy debate in legal theory * Underdeterminacy (law) Linguistics * Indeterminacy of translation * Referential indeterminacy Philosophy *Indeterminacy (philosophy) *Indeterminism, the belief that not all events are causally determined *Deterministic system (philosophy) *Underdetermination Physics *Quantum indeterminacy *Uncertainty principle *Scientific determinism Other * Indeterminacy (literature) a literary term * Indeterminacy in computation (other) * Indeterminate system * Aleatoric music and indeterminacy in music * Statically indeterminate * Underdetermined system * In set theory and game theory, the opposite of determinacy * In biology, indeterminate growth of an organism See also *Nondeterminism (other) * Determinism (other) *Indeterminate (other) Indeterminate may refer to: In mathematics * Indeterminate (variable), a symbol that is treated as a variable * Indetermin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Underdetermined System
In mathematics, a system of linear equations or a system of polynomial equations is considered underdetermined if there are fewer equations than unknowns (in contrast to an overdetermined system, where there are more equations than unknowns). The terminology can be explained using the concept of constraint counting. Each unknown can be seen as an available degree of freedom. Each equation introduced into the system can be viewed as a constraint that restricts one degree of freedom. Therefore, the critical case (between overdetermined and underdetermined) occurs when the number of equations and the number of free variables are equal. For every variable giving a degree of freedom, there exists a corresponding constraint removing a degree of freedom. The underdetermined case, by contrast, occurs when the system has been underconstrained—that is, when the unknowns outnumber the equations. Solutions of underdetermined systems An underdetermined linear system has either no sol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sparse Matrix
In numerical analysis and scientific computing, a sparse matrix or sparse array is a matrix in which most of the elements are zero. There is no strict definition regarding the proportion of zero-value elements for a matrix to qualify as sparse but a common criterion is that the number of non-zero elements is roughly equal to the number of rows or columns. By contrast, if most of the elements are non-zero, the matrix is considered dense. The number of zero-valued elements divided by the total number of elements (e.g., ''m'' × ''n'' for an ''m'' × ''n'' matrix) is sometimes referred to as the sparsity of the matrix. Conceptually, sparsity corresponds to systems with few pairwise interactions. For example, consider a line of balls connected by springs from one to the next: this is a sparse system as only adjacent balls are coupled. By contrast, if the same line of balls were to have springs connecting each ball to all other balls, the system would correspond to a dense matrix. The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Basis Pursuit
Basis pursuit is the mathematical optimization problem of the form : \min_x \, x\, _1 \quad \text \quad y = Ax, where ''x'' is a ''N''-dimensional solution vector (signal), ''y'' is a ''M''-dimensional vector of observations (measurements), ''A'' is a ''M'' × ''N'' transform matrix (usually measurement matrix) and ''M'' < ''N''. It is usually applied in cases where there is an underdetermined system of linear equations ''y'' = ''Ax'' that must be exactly satisfied, and the sparsest solution in the ''L''1 sense is desired. When it is desirable to trade off exact equality of ''Ax'' and ''y'' in exchange for a sparser ''x'', is preferred. Basis pursuit problems can be converted to |
Journal Of The Royal Statistical Society, Series B
The ''Journal of the Royal Statistical Society'' is a peer-reviewed scientific journal of statistics. It comprises three series and is published by Wiley for the Royal Statistical Society. History The Statistical Society of London was founded in 1834, but would not begin producing a journal for four years. From 1834 to 1837, members of the society would read the results of their studies to the other members, and some details were recorded in the proceedings. The first study reported to the society in 1834 was a simple survey of the occupations of people in Manchester, England. Conducted by going door-to-door and inquiring, the study revealed that the most common profession was mill-hands, followed closely by weavers. When founded, the membership of the Statistical Society of London overlapped almost completely with the statistical section of the British Association for the Advancement of Science. In 1837 a volume of ''Transactions of the Statistical Society of London'' were wri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Robert Tibshirani
Robert Tibshirani (born July 10, 1956) is a professor in the Departments of Statistics and Biomedical Data Science at Stanford University. He was a professor at the University of Toronto from 1985 to 1998. In his work, he develops statistical tools for the analysis of complex datasets, most recently in genomics and proteomics. His most well-known contributions are the Lasso method, which proposed the use of L1 penalization in regression and related problems, and Significance Analysis of Microarrays. Education and early life Tibshirani was born on 10 July 1956 in Niagara Falls, Ontario, Canada. He received his B. Math. in statistics and computer science from the University of Waterloo in 1979 and a Master's degree in Statistics from University of Toronto in 1980. Tibshirani joined the doctoral program at Stanford University in 1981 and received his Ph.D. in 1984 under the supervision of Bradley Efron. His dissertation was entitled "Local likelihood estimation". Honors and a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lasso Regression
In statistics and machine learning, lasso (least absolute shrinkage and selection operator; also Lasso or LASSO) is a regression analysis method that performs both variable selection and regularization in order to enhance the prediction accuracy and interpretability of the resulting statistical model. It was originally introduced in geophysics, and later by Robert Tibshirani, who coined the term. Lasso was originally formulated for linear regression models. This simple case reveals a substantial amount about the estimator. These include its relationship to ridge regression and best subset selection and the connections between lasso coefficient estimates and so-called soft thresholding. It also reveals that (like standard linear regression) the coefficient estimates do not need to be unique if covariates are collinear. Though originally defined for linear regression, lasso regularization is easily extended to other statistical models including generalized linear models, generaliz ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
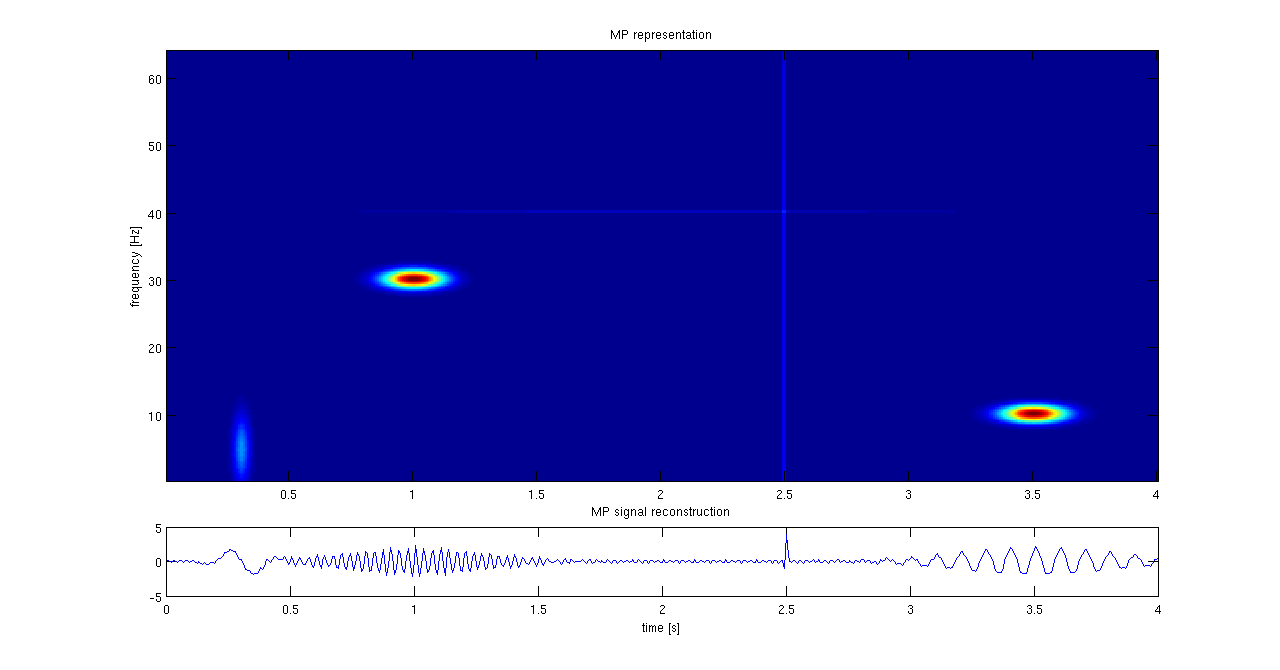
Matching Pursuit
Matching pursuit (MP) is a sparse approximation algorithm which finds the "best matching" projections of multidimensional data onto the span of an over-complete (i.e., redundant) dictionary D. The basic idea is to approximately represent a signal f from Hilbert space H as a weighted sum of finitely many functions g_ (called atoms) taken from D. An approximation with N atoms has the form : f(t) \approx \hat f_N(t) := \sum_^ a_n g_(t) where g_ is the \gamma_nth column of the matrix D and a_n is the scalar weighting factor (amplitude) for the atom g_. Normally, not every atom in D will be used in this sum. Instead, matching pursuit chooses the atoms one at a time in order to maximally (greedily) reduce the approximation error. This is achieved by finding the atom that has the highest inner product with the signal (assuming the atoms are normalized), subtracting from the signal an approximation that uses only that one atom, and repeating the process until the signal is satisfactorily d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Robust Statistics
Robust statistics are statistics with good performance for data drawn from a wide range of probability distributions, especially for distributions that are not normal. Robust statistical methods have been developed for many common problems, such as estimating location, scale, and regression parameters. One motivation is to produce statistical methods that are not unduly affected by outliers. Another motivation is to provide methods with good performance when there are small departures from a parametric distribution. For example, robust methods work well for mixtures of two normal distributions with different standard deviations; under this model, non-robust methods like a t-test work poorly. Introduction Robust statistics seek to provide methods that emulate popular statistical methods, but which are not unduly affected by outliers or other small departures from Statistical assumption, model assumptions. In statistics, classical estimation methods rely heavily on assumpti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Median-unbiased Estimator
In statistics and probability theory, the median is the value separating the higher half from the lower half of a Sample (statistics), data sample, a statistical population, population, or a probability distribution. For a data set, it may be thought of as "the middle" value. The basic feature of the median in describing data compared to the Arithmetic mean, mean (often simply described as the "average") is that it is not Skewness, skewed by a small proportion of extremely large or small values, and therefore provides a better representation of a "typical" value. Median income, for example, may be a better way to suggest what a "typical" income is, because income distribution can be very skewed. The median is of central importance in robust statistics, as it is the most resistant statistic, having a breakdown point of 50%: so long as no more than half the data are contaminated, the median is not an arbitrarily large or small result. Finite data set of numbers The median of a fin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
