|
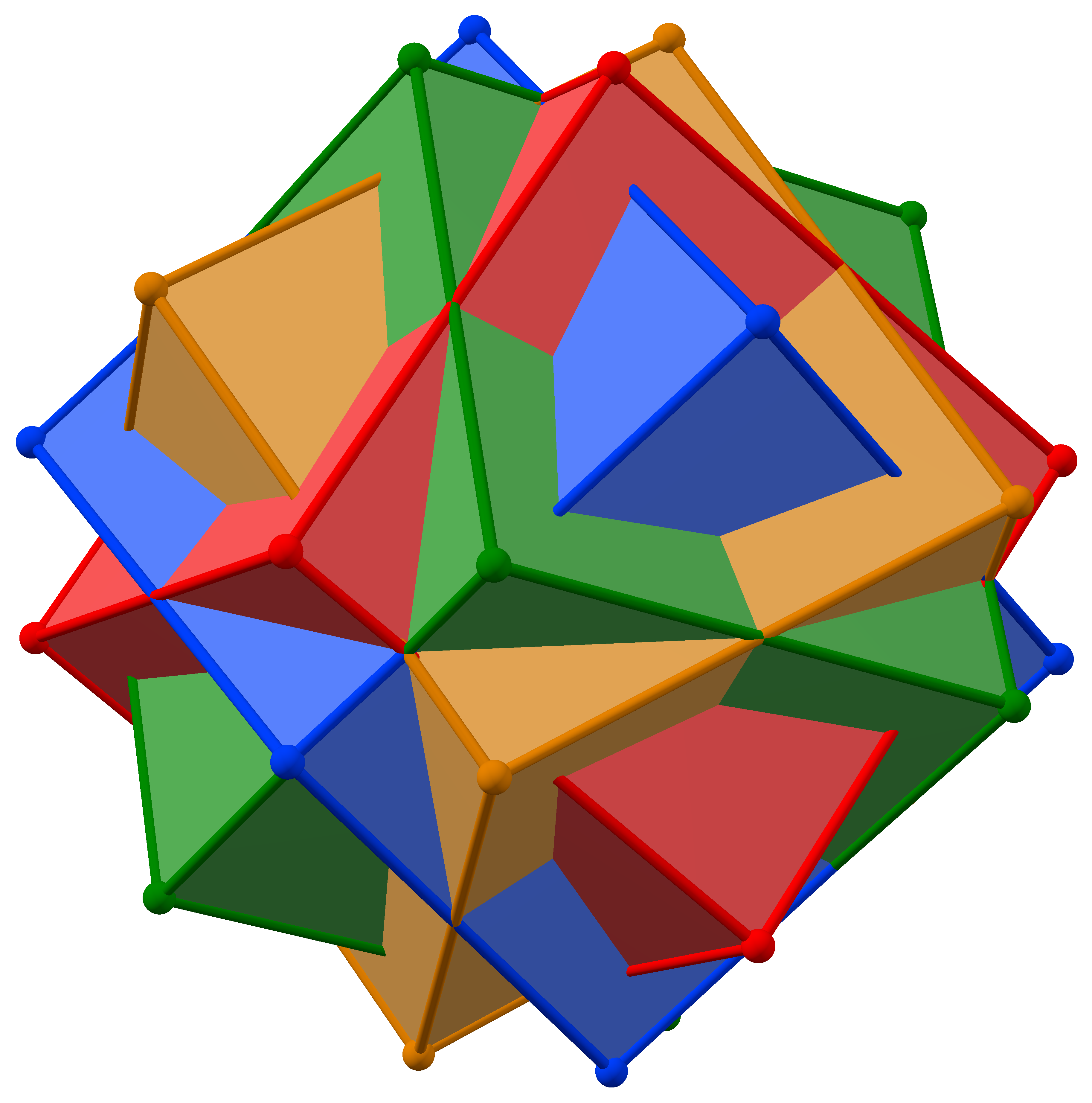
Compound Of Four Cubes
The compound of four cubes or Bakos compound is a face-transitive polyhedron compound of four cubes with octahedral symmetry. It is the dual of the compound of four octahedra. Its surface area is 687/77 square lengths of the edge. Its Cartesian coordinates are (±3, ±3, ±3) and the permutations of (±5, ±1, ±1). Extension with fifth cube The eight vertices on the 3-fold symmetry axes can be seen as the vertices of a fifth cube of the same size.The Wolfram pagCube 5-Compoundshows a small picture of this extension under the name "first cube 4-compound". Also Grant Sanderson has used a picture of it to illustrate the term ''symmetry''. Referring to the images below, the four old cubes are called colored, and the new one black. Each colored cube has two opposite vertices on a 3-fold symmetry axis, which are shared with the black cube. (In the picture both 3-fold vertices of the green cube are visible.) The remaining six vertices of each colored cube correspond to the faces of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compound Of Four Cubes
The compound of four cubes or Bakos compound is a face-transitive polyhedron compound of four cubes with octahedral symmetry. It is the dual of the compound of four octahedra. Its surface area is 687/77 square lengths of the edge. Its Cartesian coordinates are (±3, ±3, ±3) and the permutations of (±5, ±1, ±1). Extension with fifth cube The eight vertices on the 3-fold symmetry axes can be seen as the vertices of a fifth cube of the same size.The Wolfram pagCube 5-Compoundshows a small picture of this extension under the name "first cube 4-compound". Also Grant Sanderson has used a picture of it to illustrate the term ''symmetry''. Referring to the images below, the four old cubes are called colored, and the new one black. Each colored cube has two opposite vertices on a 3-fold symmetry axis, which are shared with the black cube. (In the picture both 3-fold vertices of the green cube are visible.) The remaining six vertices of each colored cube correspond to the faces of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
3Blue1Brown
3Blue1Brown is a math YouTube channel created and run by Grant Sanderson. The channel focuses on teaching higher mathematics from a visual perspective, and on the process of discovery and inquiry-based learning in mathematics, which Sanderson calls "inventing math". , the channel has 4.89 million subscribers. Early life and education Sanderson graduated from Stanford University in 2015 with a bachelor's degree in math. He worked for Khan Academy from 2015 to 2016 as part of their content fellowship program, producing videos and articles about multivariable calculus, after which he started focusing his full attention on 3Blue1Brown. Career 3Blue1Brown started as a personal programming project in early 2015. In a podcast of ''Showmakers'', Sanderson explained that he wanted to practice his coding skills and decided to make a graphics library in Python, which eventually became the open-source project "Manim" (short for Mathematical Animation engine). To have a goal for the project ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compound Of Six Cubes
A compound of six cubes has two forms. One form is a symmetric arrangement of six cubes, considered as square prisms. It is a special case of the compound of six cubes with rotational freedom. Another form is not related to a compound of six cubes with rotational freedom. See also *Compound of three cubes *Compound of five cubes *Compound of four cubes The compound of four cubes or Bakos compound is a face-transitive polyhedron compound of four cubes with octahedral symmetry. It is the dual of the compound of four octahedra. Its surface area is 687/77 square lengths of the edge. Its Cartesian ... * Compound of six octahedra References Polyhedral compounds {{polyhedron-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compound Of Five Cubes
The compound of five cubes is one of the five regular polyhedral compounds. It was first described by Edmund Hess in 1876. It is one of five regular compounds, and dual to the compound of five octahedra. It can be seen as a faceting of a regular dodecahedron. It is one of the stellations of the rhombic triacontahedron. It has icosahedral symmetry (Ih). Geometry The compound is a faceting of a dodecahedron (where pentagrams can be seen correlating to the pentagonal faces). Each cube represents a selection of 8 of the 20 vertices of the dodecahedron. If the shape is considered as a union of five cubes yielding a simple nonconvex solid without self-intersecting surfaces, then it has 360 faces (all triangles), 182 vertices (60 with degree 3, 30 with degree 4, 12 with degree 5, 60 with degree 8, and 20 with degree 12), and 540 edges, yielding an Euler characteristic of 182 − 540 + 360 = 2. Edge arrangement Its convex hull is a regular dodecahedron. It additionally shares ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compound Of Three Cubes
In geometry, the compound of three cubes is a uniform polyhedron compound formed from three cubes arranged with octahedral symmetry. It has been depicted in works by Max Brückner and M.C. Escher. History This compound appears in Max Brückner's book ''Vielecke und Vielflache'' (1900), and in the lithograph print ''Waterfall'' (1961) by M.C. Escher, who learned of it from Brückner's book. Its dual, the compound of three octahedra, forms the central image in an earlier Escher woodcut, ''Stars''. In the 15th-century manuscript ''De quinque corporibus regularibus'', Piero della Francesca includes a drawing of an octahedron circumscribed around a cube, with eight of the cube edges lying in the octahedron's eight faces. Three cubes inscribed in this way within a single octahedron would form the compound of three cubes, but della Francesca does not depict the compound. Construction and coordinates This compound can be constructed by superimposing three identical cubes, and then ro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compound Of Twenty Octahedra
The compound of twenty octahedra is a uniform polyhedron compound. It's composed of a symmetric arrangement of 20 octahedra (considered as triangular antiprisms). It is a special case of the compound of 20 octahedra with rotational freedom, in which pairs of octahedral vertices coincide. Related polyhedra This compound shares its edge arrangement with the great dirhombicosidodecahedron, the great disnub dirhombidodecahedron, and the compound of twenty tetrahemihexahedra. It may be constructed as the exclusive or of the two enantiomorphs of the great snub dodecicosidodecahedron. See also *Compound of three octahedra *Compound of four octahedra *Compound of five octahedra The compound of five octahedra is one of the five regular polyhedron compounds. This polyhedron can be seen as either a polyhedral stellation or a compound. This compound was first described by Edmund Hess in 1876. It is unique among the regular ... * Compound of ten octahedra References *. Polyhe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compound Of Ten Octahedra
The compounds of ten octahedra UC15 and UC16 are two uniform polyhedron compounds. They are composed of a symmetric arrangement of 10 octahedron, octahedra, considered as triangular antiprisms, aligned with the axes of three-fold rotational symmetry of an icosahedron. The two compounds differ in the orientation of their octahedra: each compound may be transformed into the other by rotating each octahedron by 60 degrees. Cartesian coordinates Cartesian coordinates for the vertices of this compound are all the cyclic permutations of : (0, ±(τ−1 + 2''s''τ), ±(τ − 2sτ−1)) : (±( − ''s''τ2), ±( + ''s''(2τ − 1)), ±( + ''s''τ−2)) : (±(τ−1 − ''s''τ), ±(τ + ''s''τ−1), ±3''s'') where τ = (1 + )/2 is the golden ratio (sometimes written φ) and ''s'' is either +1 or −1. Setting ''s'' = −1 gives UC15, while ''s'' = +1 gives UC16. See also *Compound of three octahedra *Compound of four octahedra *Compound ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compound Of Five Octahedra
The compound of five octahedra is one of the five regular polyhedron compounds. This polyhedron can be seen as either a polyhedral stellation or a compound. This compound was first described by Edmund Hess in 1876. It is unique among the regular compounds for not having a regular convex hull. As a stellation It is the second stellation of the icosahedron, and given as Wenninger model index 23. It can be constructed by a rhombic triacontahedron with rhombic-based pyramids added to all the faces, as shown by the five colored model image. (This construction does not generate the ''regular'' compound of five octahedra, but shares the same topology and can be smoothly deformed into the regular compound.) It has a density of greater than 1. As a compound It can also be seen as a polyhedral compound of five octahedra arranged in icosahedral symmetry (Ih). The spherical and stereographic projections of this compound look the same as those of the disdyakis triacontahedron. But ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compound Of Three Octahedra
In mathematics, the compound of three octahedra or octahedron 3-compound is a polyhedral compound formed from three regular octahedra, all sharing a common center but rotated with respect to each other. Although appearing earlier in the mathematical literature, it was rediscovered and popularized by M. C. Escher, who used it in the central image of his 1948 woodcut ''Stars''. Construction A regular octahedron can be circumscribed around a cube in such a way that the eight edges of two opposite squares of the cube lie on the eight faces of the octahedron. The three octahedra formed in this way from the three pairs of opposite cube squares form the compound of three octahedra.. The eight cube vertices are the same as the eight points in the compound where three edges cross each other. Each of the octahedron edges that participates in these triple crossings is divided by the crossing point in the ratio 1: . The remaining octahedron edges cross each other in pairs, within the interior ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regular Dodecahedron
A regular dodecahedron or pentagonal dodecahedron is a dodecahedron that is regular, which is composed of 12 regular pentagonal faces, three meeting at each vertex. It is one of the five Platonic solids. It has 12 faces, 20 vertices, 30 edges, and 160 diagonals (60 face diagonals, 100 space diagonals). It is represented by the Schläfli symbol . Dimensions If the edge length of a regular dodecahedron is a, the radius of a circumscribed sphere (one that touches the regular dodecahedron at all vertices) is :r_u = a\frac \left(1 + \sqrt\right) \approx 1.401\,258\,538 \cdot a and the radius of an inscribed sphere (tangent to each of the regular dodecahedron's faces) is :r_i = a\frac \sqrt \approx 1.113\,516\,364 \cdot a while the midradius, which touches the middle of each edge, is :r_m = a\frac \left(3 +\sqrt\right) \approx 1.309\,016\,994 \cdot a These quantities may also be expressed as :r_u = a\, \frac \phi :r_i = a\, \frac :r_m = a\, \frac where ''ϕ'' is the golden rat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compound Of Five Cubes
The compound of five cubes is one of the five regular polyhedral compounds. It was first described by Edmund Hess in 1876. It is one of five regular compounds, and dual to the compound of five octahedra. It can be seen as a faceting of a regular dodecahedron. It is one of the stellations of the rhombic triacontahedron. It has icosahedral symmetry (Ih). Geometry The compound is a faceting of a dodecahedron (where pentagrams can be seen correlating to the pentagonal faces). Each cube represents a selection of 8 of the 20 vertices of the dodecahedron. If the shape is considered as a union of five cubes yielding a simple nonconvex solid without self-intersecting surfaces, then it has 360 faces (all triangles), 182 vertices (60 with degree 3, 30 with degree 4, 12 with degree 5, 60 with degree 8, and 20 with degree 12), and 540 edges, yielding an Euler characteristic of 182 − 540 + 360 = 2. Edge arrangement Its convex hull is a regular dodecahedron. It additionally shares ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |