|
Composite Field
In quantum field theory, a composite field is a field defined in terms of other more "elementary" fields. It might describe a composite particle (bound state) or it might not. It might be local, or it might be nonlocal. However, "quantum fields do not exist as a point taken in isolation," so "local" does not mean literally a single point. Composite fields use a very specific kind of statistics, called "duality and arbitrary statistics". Under Noether's theorem, Noether fields are often composite fields, and they are local. In the generalized LSZ formalism, composite fields, which are usually nonlocal, are used to model asymptotic bound states. See also * Fermionic field In quantum field theory, a fermionic field is a quantum field whose quanta are fermions; that is, they obey Fermi–Dirac statistics. Fermionic fields obey canonical anticommutation relations rather than the canonical commutation relations of ... * Bosonic field * Auxiliary field References ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Field Theory
In theoretical physics, quantum field theory (QFT) is a theoretical framework that combines Field theory (physics), field theory and the principle of relativity with ideas behind quantum mechanics. QFT is used in particle physics to construct physical models of subatomic particles and in condensed matter physics to construct models of quasiparticles. The current standard model of particle physics is based on QFT. History Quantum field theory emerged from the work of generations of theoretical physicists spanning much of the 20th century. Its development began in the 1920s with the description of interactions between light and electrons, culminating in the first quantum field theory—quantum electrodynamics. A major theoretical obstacle soon followed with the appearance and persistence of various infinities in perturbative calculations, a problem only resolved in the 1950s with the invention of the renormalization procedure. A second major barrier came with QFT's apparent inabili ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Composite Particle
This is a list of known and hypothesized microscopic particles in particle physics, condensed matter physics and cosmology. Standard Model elementary particles Elementary particles are particles with no measurable internal structure; that is, it is unknown whether they are composed of other particles. They are the fundamental objects of quantum field theory. Many families and sub-families of elementary particles exist. Elementary particles are classified according to their Spin (physics), spin. Fermions have half-integer spin while bosons have integer spin. All the elementary particles of the Standard Model have been experimentally observed, including the Higgs boson in 2012. Many other hypothetical elementary particles, such as the graviton, have been proposed, but not observed experimentally. Fermions Fermions are one of the two fundamental classes of particles, the other being bosons. Fermion particles are described by Fermi–Dirac statistics and have quantum numbers de ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bound State
A bound state is a composite of two or more fundamental building blocks, such as particles, atoms, or bodies, that behaves as a single object and in which energy is required to split them. In quantum physics, a bound state is a quantum state of a particle subject to a potential energy, potential such that the particle has a tendency to remain localized in one or more regions of space. The potential may be external or it may be the result of the presence of another particle; in the latter case, one can equivalently define a bound state as a state representing two or more particles whose interaction energy exceeds the total energy of each separate particle. One consequence is that, given a potential vanish at infinity, vanishing at infinity, negative-energy states must be bound. The energy spectrum of the set of bound states are most commonly discrete, unlike scattering states of Free particle, free particles, which have a continuous spectrum. Although not bound states in the stric ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Principle Of Locality
In physics, the principle of locality states that an object is influenced directly only by its immediate surroundings. A theory that includes the principle of locality is said to be a "local theory". This is an alternative to the concept of instantaneous, or "non-local" action at a distance. Locality evolved out of the Classical field theory, field theories of classical physics. The idea is that for a cause at one point to have an effect at another point, something in the space between those points must mediate the action. To exert an influence, something, such as a wave or particle, must travel through the space between the two points, carrying the influence. The special relativity, special theory of relativity limits the maximum speed at which causal influence can travel to the speed of light, c. Therefore, the principle of locality implies that an event at one point cannot cause a truly simultaneous result at another point. An event at point A cannot cause a result at point B ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
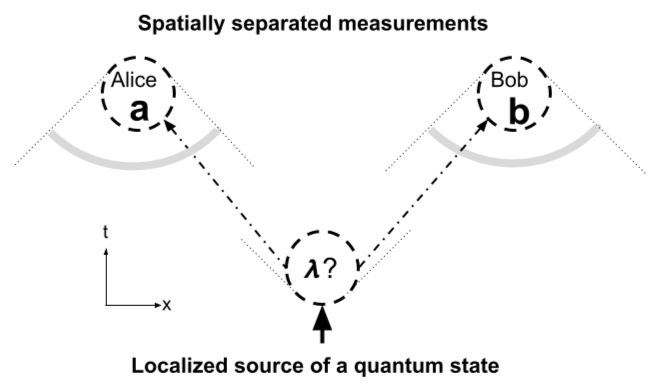
Quantum Nonlocality
In theoretical physics, quantum nonlocality refers to the phenomenon by which the measurement statistics of a multipartite quantum system do not allow an interpretation with local realism. Quantum nonlocality has been experimentally verified under a variety of physical assumptions. Quantum nonlocality does not allow for faster-than-light communication, and hence is compatible with special relativity and its universal speed limit of objects. Thus, quantum theory is local in the strict sense defined by special relativity and, as such, the term "quantum nonlocality" is sometimes considered a misnomer. Still, it prompts many of the foundational discussions concerning quantum theory. History Einstein, Podolsky and Rosen In the 1935 EPR paper, Albert Einstein, Boris Podolsky and Nathan Rosen described "two spatially separated particles which have both perfectly correlated positions and momenta" as a direct consequence of quantum theory. They intended to use the classical princip ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German language, German: ', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of statistical survey, surveys and experimental design, experiments. When census data (comprising every member of the target population) cannot be collected, statisticians collect data by developing specific experiment designs and survey sample (statistics), samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Noether's Theorem
Noether's theorem states that every continuous symmetry of the action of a physical system with conservative forces has a corresponding conservation law. This is the first of two theorems (see Noether's second theorem) published by the mathematician Emmy Noether in 1918. The action of a physical system is the integral over time of a Lagrangian function, from which the system's behavior can be determined by the principle of least action. This theorem applies to continuous and smooth symmetries of physical space. Noether's formulation is quite general and has been applied across classical mechanics, high energy physics, and recently statistical mechanics. Noether's theorem is used in theoretical physics and the calculus of variations. It reveals the fundamental relation between the symmetries of a physical system and the conservation laws. It also made modern theoretical physicists much more focused on symmetries of physical systems. A generalization of the formulations ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Noether Field
Noether is the family name of several mathematicians (particularly, the Noether family), and the name given to some of their mathematical contributions: * Max Noether (1844–1921), German mathematician * Emmy Noether (1882–1935), German mathematician ** Nöther crater, on the far side of the Moon, named after Emmy Noether * Fritz Noether (1884–1941), professor at the University of Tomsk * Gottfried E. Noether (1915–1991), son of Fritz Noether, statistician at the University of Connecticut See also * Noether's theorem (other) * List of things named after Emmy Noether Emmy Noether (1882–1935) was a German mathematician who made many important contributions to abstract algebra. This article is dedicated to the things named after her achievements. Mathematics "Noetherian" * Noetherian * Noetherian group * No ... {{surname, Noether Surnames of Jewish origin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
LSZ Formalism
In quantum field theory, the Lehmann–Symanzik–Zimmermann (LSZ) reduction formula is a method to calculate ''S''-matrix elements (the scattering amplitudes) from the time-ordered correlation functions of a quantum field theory. It is a step of the path that starts from the Lagrangian of some quantum field theory and leads to prediction of measurable quantities. It is named after the three German physicists Harry Lehmann, Kurt Symanzik and Wolfhart Zimmermann. Although the LSZ reduction formula cannot handle bound states, massless particles and topological solitons, it can be generalized to cover bound states, by use of composite fields which are often nonlocal. Furthermore, the method, or variants thereof, have turned out to be also fruitful in other fields of theoretical physics. For example, in statistical physics they can be used to get a particularly general formulation of the fluctuation-dissipation theorem. In and out fields ''S''-matrix elements are probability ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Asymptotic
In analytic geometry, an asymptote () of a curve is a line such that the distance between the curve and the line approaches zero as one or both of the ''x'' or ''y'' coordinates Limit of a function#Limits at infinity, tends to infinity. In projective geometry and related contexts, an asymptote of a curve is a line which is tangent to the curve at a point at infinity. The word asymptote is derived from the Greek language, Greek ἀσύμπτωτος (''asumptōtos'') which means "not falling together", from ἀ Privative alpha, priv. + σύν "together" + πτωτ-ός "fallen". The term was introduced by Apollonius of Perga in his work on conic sections, but in contrast to its modern meaning, he used it to mean any line that does not intersect the given curve. There are three kinds of asymptotes: ''horizontal'', ''vertical'' and ''oblique''. For curves given by the graph of a function, graph of a function (mathematics), function , horizontal asymptotes are horizontal lines tha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fermionic Field
In quantum field theory, a fermionic field is a quantum field whose quanta are fermions; that is, they obey Fermi–Dirac statistics. Fermionic fields obey canonical anticommutation relations rather than the canonical commutation relations of bosonic fields. The most prominent example of a fermionic field is the ''Dirac field'', which describes fermions with spin-1/2: electrons, protons, quarks, etc. The Dirac field can be described as either a 4-component spinor or as a pair of 2-component Weyl spinors. Spin-1/2 Majorana fermions, such as the hypothetical neutralino, can be described as either a dependent 4-component Majorana spinor or a single 2-component Weyl spinor. It is not known whether the neutrino is a Majorana fermion or a Dirac fermion; observing neutrinoless double-beta decay experimentally would settle this question. Basic properties Free (non-interacting) fermionic fields obey canonical anticommutation relations; i.e., involve the anticommutators = ''ab'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bosonic Field
In quantum field theory, a bosonic field is a quantum field whose quanta are bosons; that is, they obey Bose–Einstein statistics. Bosonic fields obey canonical commutation relations, as distinct from the canonical anticommutation relations obeyed by fermionic fields. Examples include scalar fields, describing spin-0 particles such as the Higgs boson, and gauge fields, describing spin-1 particles such as the photon. Basic properties Free (non-interacting) bosonic fields obey canonical commutation relations. Those relations also hold for interacting bosonic fields in the interaction picture, where the fields evolve in time as if free and the effects of the interaction are encoded in the evolution of the states. It is these commutation relations that imply Bose–Einstein statistics for the field quanta. Examples Examples of bosonic fields include scalar fields, gauge fields, and symmetric 2-tensor fields, which are characterized by their covariance under Lorentz transformat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |