|
Composite Boson
A composite boson is a bound state of fermions such that the combination gives a boson.Monique Combescot and Shiue-Yuan Shiau, "Excitons and Cooper Pairs: Two Composite Bosons in Many-Body Physics", Oxford University Press (). Examples include Cooper pairs, semiconductor excitons, mesons, superfluid helium, Bose–Einstein condensates, atomic bosons, and fermionic condensates. A composite particle containing an even number of fermions is a boson, since it has integer spin. These composite particle states have a symmetric wave function upon exchange of any pair of particles. The wave function is given by the permanent of single particle states for the non interacting case. See also * Composite fermion References * University of Colorado (January 28, 2004). ''NIST/University of Colorado Scientists Create New Form of Matter: A Fermionic Condensate''. Press Release. * Rodgers, Peter & Dumé, Bell (January 28, 2004). ''Fermionic condensate makes its debut''. PhysicWeb. * Haegler, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fermion
In particle physics, a fermion is a particle that follows Fermi–Dirac statistics. Generally, it has a half-odd-integer spin: spin , spin , etc. In addition, these particles obey the Pauli exclusion principle. Fermions include all quarks and leptons and all composite particles made of an odd number of these, such as all baryons and many atoms and nuclei. Fermions differ from bosons, which obey Bose–Einstein statistics. Some fermions are elementary particles (such as electrons), and some are composite particles (such as protons). For example, according to the spin-statistics theorem in relativistic quantum field theory, particles with integer spin are bosons. In contrast, particles with half-integer spin are fermions. In addition to the spin characteristic, fermions have another specific property: they possess conserved baryon or lepton quantum numbers. Therefore, what is usually referred to as the spin-statistics relation is, in fact, a spin statistics-quantum numb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cooper Pair
In condensed matter physics, a Cooper pair or BCS pair (Bardeen–Cooper–Schrieffer pair) is a pair of electrons (or other fermions) bound together at low temperatures in a certain manner first described in 1956 by American physicist Leon Cooper. Cooper pair Cooper showed that an arbitrarily small attraction between electrons in a metal can cause a paired state of electrons to have a lower energy than the Fermi energy, which implies that the pair is bound. In conventional superconductors, this attraction is due to the electron–phonon interaction. The Cooper pair state is responsible for superconductivity, as described in the BCS theory developed by John Bardeen, Leon Cooper, and John Schrieffer for which they shared the 1972 Nobel Prize. Although Cooper pairing is a quantum effect, the reason for the pairing can be seen from a simplified classical explanation. An electron in a metal normally behaves as a free particle. The electron is repelled from other electrons due to thei ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exciton
An exciton is a bound state of an electron and an electron hole which are attracted to each other by the electrostatic Coulomb force. It is an electrically neutral quasiparticle that exists in insulators, semiconductors and some liquids. The exciton is regarded as an elementary excitation of condensed matter that can transport energy without transporting net electric charge. An exciton can form when a material absorbs a photon of higher energy than its bandgap. This excites an electron from the valence band into the conduction band. In turn, this leaves behind a positively charged electron hole (an abstraction for the location from which an electron was moved). The electron in the conduction band is then less attracted to this localized hole due to the repulsive Coulomb forces from large numbers of electrons surrounding the hole and excited electron. These repulsive forces provide a stabilizing energy balance. Consequently, the exciton has slightly less energy than the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Meson
In particle physics, a meson ( or ) is a type of hadronic subatomic particle composed of an equal number of quarks and antiquarks, usually one of each, bound together by the strong interaction. Because mesons are composed of quark subparticles, they have a meaningful physical size, a diameter of roughly one femtometre (10 m), which is about 0.6 times the size of a proton or neutron. All mesons are unstable, with the longest-lived lasting for only a few hundredths of a microsecond. Heavier mesons decay to lighter mesons and ultimately to stable electrons, neutrinos and photons. Outside the nucleus, mesons appear in nature only as short-lived products of very high-energy collisions between particles made of quarks, such as cosmic rays (high-energy protons and neutrons) and baryonic matter. Mesons are routinely produced artificially in cyclotrons or other particle accelerators in the collisions of protons, antiprotons, or other particles. Higher-energy (more massive) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
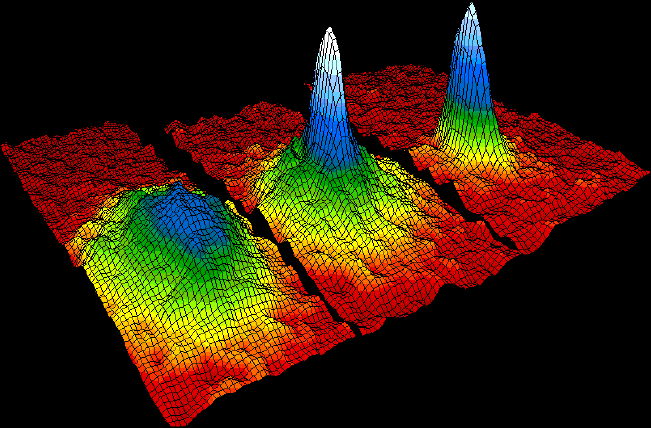
Bose–Einstein Condensate
In condensed matter physics, a Bose–Einstein condensate (BEC) is a state of matter that is typically formed when a gas of bosons at very low densities is cooled to temperatures very close to absolute zero (−273.15 °C or −459.67 °F). Under such conditions, a large fraction of bosons occupy the lowest quantum state, at which point microscopic quantum mechanical phenomena, particularly wavefunction interference, become apparent macroscopically. A BEC is formed by cooling a gas of extremely low density (about 100,000 times less dense than normal air) to ultra-low temperatures. This state was first predicted, generally, in 1924–1925 by Albert Einstein following and crediting a pioneering paper by Satyendra Nath Bose on the new field now known as quantum statistics. In 1995, the Bose-Einstein condensate was created by Eric Cornell and Carl Wieman of the University of Colorado at Boulder using rubidium atoms; later that year, Wolfgang Ketterle of MIT produc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fermionic Condensate
A fermionic condensate or Fermi–Dirac condensate is a superfluid phase formed by fermionic particles at low temperatures. It is closely related to the Bose–Einstein condensate, a superfluid phase formed by bosonic atoms under similar conditions. The earliest recognized fermionic condensate described the state of electrons in a superconductor; the physics of other examples including recent work with fermionic atoms is analogous. The first atomic fermionic condensate was created by a team led by Deborah S. Jin using potassium-40 atoms at the University of Colorado Boulder in 2003. Background Superfluidity Fermionic condensates are attained at lower temperatures than Bose–Einstein condensates. Fermionic condensates are a type of superfluid. As the name suggests, a superfluid possesses fluid properties similar to those possessed by ordinary liquids and gases, such as the lack of a definite shape and the ability to flow in response to applied forces. However, superfluids pos ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wave Function
A wave function in quantum physics is a mathematical description of the quantum state of an isolated quantum system. The wave function is a complex-valued probability amplitude, and the probabilities for the possible results of measurements made on the system can be derived from it. The most common symbols for a wave function are the Greek letters and (lower-case and capital psi, respectively). The wave function is a function of the degrees of freedom corresponding to some maximal set of commuting observables. Once such a representation is chosen, the wave function can be derived from the quantum state. For a given system, the choice of which commuting degrees of freedom to use is not unique, and correspondingly the domain of the wave function is also not unique. For instance, it may be taken to be a function of all the position coordinates of the particles over position space, or the momenta of all the particles over momentum space; the two are related by a Fourier tran ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Permanent (mathematics)
In linear algebra, the permanent of a square matrix is a function of the matrix similar to the determinant. The permanent, as well as the determinant, is a polynomial in the entries of the matrix. Both are special cases of a more general function of a matrix called the immanant. Definition The permanent of an matrix is defined as \operatorname(A)=\sum_\prod_^n a_. The sum here extends over all elements σ of the symmetric group ''S''''n''; i.e. over all permutations of the numbers 1, 2, ..., ''n''. For example, \operatorname\begina&b \\ c&d\end=ad+bc, and \operatorname\begina&b&c \\ d&e&f \\ g&h&i \end=aei + bfg + cdh + ceg + bdi + afh. The definition of the permanent of ''A'' differs from that of the determinant of ''A'' in that the signatures of the permutations are not taken into account. The permanent of a matrix A is denoted per ''A'', perm ''A'', or Per ''A'', sometimes with parentheses around the argument. Minc uses Per(''A'') for the permanent of rectangular mat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Composite Fermion
A composite fermion is the topological bound state of an electron and an even number of quantized vortices, sometimes visually pictured as the bound state of an electron and, attached, an even number of magnetic flux quanta. Composite fermions were originally envisioned in the context of the fractional quantum Hall effect, but subsequently took on a life of their own, exhibiting many other consequences and phenomena. Vortices are an example of topological defect, and also occur in other situations. Quantized vortices are found in type II superconductors, called Abrikosov vortices. Classical vortices are relevant to the Berezenskii–Kosterlitz–Thouless transition in two-dimensional XY model. Description When electrons are confined to two dimensions, cooled to very low temperatures, and subjected to a strong magnetic field, their kinetic energy is quenched due to Landau level quantization. Their behavior under such conditions is governed by the Coulomb repulsion alone, and t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |