|
Coffman–Graham Algorithm
In job shop scheduling and graph drawing, the Coffman–Graham algorithm is an algorithm, named after Edward G. Coffman, Jr. and Ronald Graham, for arranging the elements of a partially ordered set into a sequence of levels. The algorithm chooses an arrangement such that an element that comes after another in the order is assigned to a lower level, and such that each level has a number of elements that does not exceed a fixed width bound . When , it uses the minimum possible number of distinct levels, and in general it uses at most times as many levels as necessary. Problem statement and applications In the version of the job shop scheduling problem solved by the Coffman–Graham algorithm, one is given a set of jobs , together with a system of precedence constraints requiring that job be completed before job begins. Each job is assumed to take unit time to complete. The scheduling task is to assign each of these jobs to time slots on a system of identical processors, minimiz ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Job Shop Scheduling
Job-shop scheduling, the job-shop problem (JSP) or job-shop scheduling problem (JSSP) is an optimization problem in computer science and operations research. It is a variant of optimal job scheduling. In a general job scheduling problem, we are given ''n'' jobs ''J''1, ''J''2, ..., ''Jn'' of varying processing times, which need to be scheduled on ''m'' machines with varying processing power, while trying to minimize the makespan – the total length of the schedule (that is, when all the jobs have finished processing). In the specific variant known as ''job-shop scheduling'', each job consists of a set of ''operations'' ''O''1, ''O''2, ..., ''On'' which need to be processed in a specific order (known as ''precedence constraints''). Each operation has a ''specific machine'' that it needs to be processed on and only one operation in a job can be processed at a given time. A common relaxation is the flexible job shop, where each operation can be processed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
9th International Symposium, GD 2001 Vienna, Austria, September 23–26, 2001, Revised Papers
9 (nine) is the natural number following and preceding . Evolution of the Arabic digit In the beginning, various Indians wrote a digit 9 similar in shape to the modern closing question mark without the bottom dot. The Kshatrapa, Andhra and Gupta started curving the bottom vertical line coming up with a -look-alike. The Nagari continued the bottom stroke to make a circle and enclose the 3-look-alike, in much the same way that the sign @ encircles a lowercase ''a''. As time went on, the enclosing circle became bigger and its line continued beyond the circle downwards, as the 3-look-alike became smaller. Soon, all that was left of the 3-look-alike was a squiggle. The Arabs simply connected that squiggle to the downward stroke at the middle and subsequent European change was purely cosmetic. While the shape of the glyph for the digit 9 has an ascender in most modern typefaces, in typefaces with text figures the character usually has a descender, as, for example, in . The mod ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Disjoint-set Data Structure
In computer science, a disjoint-set data structure, also called a union–find data structure or merge–find set, is a data structure that stores a collection of Disjoint sets, disjoint (non-overlapping) Set (mathematics), sets. Equivalently, it stores a partition of a set into disjoint subsets. It provides operations for adding new sets, merging sets (replacing them by their Union (set theory), union), and finding a representative member of a set. The last operation makes it possible to find out efficiently if any two elements are in the same or different sets. While there are several ways of implementing disjoint-set data structures, in practice they are often identified with a particular implementation called a disjoint-set forest. This is a specialized type of Forest (graph theory), forest which performs unions and finds in near-constant Amortized analysis, amortized time. To perform a sequence of addition, union, or find operations on a disjoint-set forest with node ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partition Refinement
In the design of algorithms, partition refinement is a technique for representing a partition of a set as a data structure that allows the partition to be refined by splitting its sets into a larger number of smaller sets. In that sense it is dual to the union-find data structure, which also maintains a partition into disjoint sets but in which the operations merge pairs of sets. In some applications of partition refinement, such as lexicographic breadth-first search, the data structure maintains as well an ordering on the sets in the partition. Partition refinement forms a key component of several efficient algorithms on graphs and finite automata, including DFA minimization, the Coffman–Graham algorithm for parallel scheduling, and lexicographic breadth-first search of graphs. Data structure A partition refinement algorithm maintains a family of disjoint sets . At the start of the algorithm, this family contains a single set of all the elements in the data structure. At e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Time
In computer science, the time complexity is the computational complexity that describes the amount of computer time it takes to run an algorithm. Time complexity is commonly estimated by counting the number of elementary operations performed by the algorithm, supposing that each elementary operation takes a fixed amount of time to perform. Thus, the amount of time taken and the number of elementary operations performed by the algorithm are taken to be related by a constant factor. Since an algorithm's running time may vary among different inputs of the same size, one commonly considers the worst-case time complexity, which is the maximum amount of time required for inputs of a given size. Less common, and usually specified explicitly, is the average-case complexity, which is the average of the time taken on inputs of a given size (this makes sense because there are only a finite number of possible inputs of a given size). In both cases, the time complexity is generally expresse ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Total Flow Time
Total may refer to: Mathematics * Total, the summation of a set of numbers * Total order, a partial order without incomparable pairs * Total relation, which may also mean ** connected relation (a binary relation in which any two elements are comparable). * Total function, a partial function that is also a total relation Business * TotalEnergies, a French petroleum company * Total (cereal), a food brand by General Mills * Total, a brand of strained yogurt made by Fage * Total, a database management system marketed by Cincom Systems * Total Linhas Aéreas - a brazilian airline * Total, a line of dental products by Colgate Music and culture * Total (group), an American R&B girl group * '' Total: From Joy Division to New Order'', a compilation album * ''Total'' (Sebastian album) * ''Total'' (Total album) * ''Total'' (Teenage Bottlerocket album) * ''Total'' (Seigmen album) * ''Total'' (Wanessa album) * ''Total'' (Belinda Peregrín album) * ''Total 1'', an annual compilation alb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
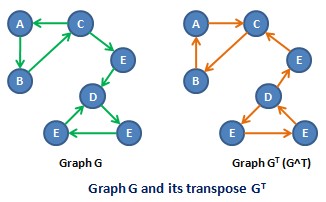
Reverse Graph
In the mathematical and algorithmic study of graph theory, the converse, transpose or reverse, entry 2.24 of a directed graph is another directed graph on the same set of vertices with all of the edges reversed compared to the orientation of the corresponding edges in . That is, if contains an edge then the converse/transpose/reverse of contains an edge and vice versa. Notation The name arises because the reversal of arrows corresponds to taking the converse of an implication in logic. The name is because the adjacency matrix of the transpose directed graph is the transpose of the adjacency matrix of the original directed graph. There is no general agreement on preferred terminology. The converse is denoted symbolically as , , , or other notations, depending on which terminology is used and which book or article is the source for the notation. Applications Although there is little difference mathematically between a graph and its transpose, the difference may be lar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
SIAM Journal On Discrete Mathematics
'' SIAM Journal on Discrete Mathematics'' is a peer-reviewed mathematics journal published quarterly by the Society for Industrial and Applied Mathematics (SIAM). The journal includes articles on pure and applied discrete mathematics. It was established in 1988, along with the '' SIAM Journal on Matrix Analysis and Applications'', to replace the '' SIAM Journal on Algebraic and Discrete Methods''. The journal is indexed by ''Mathematical Reviews'' and Zentralblatt MATH. Its 2009 MCQ was 0.57. According to the ''Journal Citation Reports'', the journal has a 2016 impact factor of 0.755. Although its official ISO abbreviation is ''SIAM J. Discrete Math.'', its publisher and contributors frequently use the shorter abbreviation ''SIDMA''. References External links * Combinatorics journals Publications established in 1988 English-language journals Discrete Mathematics Discrete mathematics is the study of mathematical structures that can be considered "discrete" (in a wa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Interval Order
In mathematics, especially order theory, the interval order for a collection of intervals on the real line is the partial order corresponding to their left-to-right precedence relation—one interval, ''I''1, being considered less than another, ''I''2, if ''I''1 is completely to the left of ''I''2. More formally, a countable poset P = (X, \leq) is an interval order if and only if there exists a bijection from X to a set of real intervals, so x_i \mapsto (\ell_i, r_i) , such that for any x_i, x_j \in X we have x_i , a left nesting is an i \in n/math> such that i < i+1 < f(i+1) < f(i) and a right nesting is an |
SIAM Journal On Computing
The ''SIAM Journal on Computing'' is a scientific journal focusing on the mathematical and formal aspects of computer science. It is published by the Society for Industrial and Applied Mathematics (SIAM). Although its official ISO abbreviation is ''SIAM J. Comput.'', its publisher and contributors frequently use the shorter abbreviation ''SICOMP''. SICOMP typically hosts the special issues of the IEEE Annual Symposium on Foundations of Computer Science (FOCS) and the Annual ACM Symposium on Theory of Computing (STOC), where about 15% of papers published in FOCS and STOC each year are invited to these special issues. For example, Volume 48 contains 11 out of 85 papers published in FOCS 2016. References * External linksSIAM Journal on Computing on |
IEEE Transactions On Computers
''IEEE Transactions on Computers'' is a monthly peer-reviewed scientific journal covering all aspects of computer design. It was established in 1952 and is published by the IEEE Computer Society. The editor-in-chief is Ahmed Louri, David and Marilyn Karlgaard Endowed Chair Professor of Electrical and Computer Engineering, George Washington University. According to the ''Journal Citation Reports'', the journal has a 2019 impact factor The impact factor (IF) or journal impact factor (JIF) of an academic journal is a scientometric index calculated by Clarivate that reflects the yearly mean number of citations of articles published in the last two years in a given journal, as ... of 3.131. References External links * Transactions on Computers Computer science journals English-language journals Publications established in 1952 Monthly journals {{comp-sci-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lexicographic Order
In mathematics, the lexicographic or lexicographical order (also known as lexical order, or dictionary order) is a generalization of the alphabetical order of the dictionaries to sequences of ordered symbols or, more generally, of elements of a totally ordered set. There are several variants and generalizations of the lexicographical ordering. One variant applies to sequences of different lengths by comparing the lengths of the sequences before considering their elements. Another variant, widely used in combinatorics, orders subsets of a given finite set by assigning a total order to the finite set, and converting subsets into increasing sequences, to which the lexicographical order is applied. A generalization defines an order on a Cartesian product of partially ordered sets; this order is a total order if and only if all factors of the Cartesian product are totally ordered. Motivation and definition The words in a lexicon (the set of words used in some language) have a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |