|
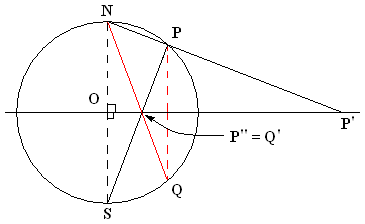
Coaxal Circles
In geometry, Apollonian circles are two families (pencils) of circles such that every circle in the first family intersects every circle in the second family orthogonally, and vice versa. These circles form the basis for bipolar coordinates. They were discovered by Apollonius of Perga, a renowned ancient Greek geometer. Definition The Apollonian circles are defined in two different ways by a line segment denoted . Each circle in the first family (the blue circles in the figure) is associated with a positive real number , and is defined as the locus of points such that the ratio of distances from to and to equals , \left\. For values of close to zero, the corresponding circle is close to , while for values of close to , the corresponding circle is close to ; for the intermediate value , the circle degenerates to a line, the perpendicular bisector of . The equation defining these circles as a locus can be generalized to define the Fermat–Apollonius circles of larger se ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radical Axis
In Euclidean geometry, the radical axis of two non-concentric circles is the set of points whose Power of a point, power with respect to the circles are equal. For this reason the radical axis is also called the power line or power bisector of the two circles. In detail: For two circles with centers and radii the powers of a point with respect to the circles are :\Pi_1(P)=, PM_1, ^2 - r_1^2,\qquad \Pi_2(P)= , PM_2, ^2 - r_2^2. Point belongs to the radical axis, if : \Pi_1(P)=\Pi_2(P). If the circles have two points in common, the radical axis is the common secant line of the circles. If point is outside the circles, has equal tangential distance to both the circles. If the radii are equal, the radical axis is the line segment bisector of . In any case the radical axis is a line perpendicular to \overline. ;On notations The notation ''radical axis'' was used by the French mathematician Michel Chasles, M. Chasles as ''axe radical''. Jean-Victor Poncelet, J.V. Poncelet us ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Collinear
In geometry, collinearity of a set of Point (geometry), points is the property of their lying on a single Line (geometry), line. A set of points with this property is said to be collinear (sometimes spelled as colinear). In greater generality, the term has been used for aligned objects, that is, things being "in a line" or "in a row". Points on a line In any geometry, the set of points on a line are said to be collinear. In Euclidean geometry this relation is intuitively visualized by points lying in a row on a "straight line". However, in most geometries (including Euclidean) a Line (geometry), line is typically a Primitive notion, primitive (undefined) object type, so such visualizations will not necessarily be appropriate. A Mathematical model, model for the geometry offers an interpretation of how the points, lines and other object types relate to one another and a notion such as collinearity must be interpreted within the context of that model. For instance, in spherical g ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elementary Geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician who works in the field of geometry is called a ''List of geometers, geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point (geometry), point, line (geometry), line, plane (geometry), plane, distance, angle, surface (mathematics), surface, and curve, as fundamental concepts. Originally developed to model the physical world, geometry has applications in almost all sciences, and also in art, architecture, and other activities that are related to graphics. Geometry also has applications in areas of mathematics that are apparently unrelated. For example, methods of algebraic geometry are fundamental in Wiles's proof of Fermat's Last Theorem, Wiles's proof of Fermat's ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circles
A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. The distance between any point of the circle and the centre is called the radius. The length of a line segment connecting two points on the circle and passing through the centre is called the diameter. A circle bounds a region of the plane called a disc. The circle has been known since before the beginning of recorded history. Natural circles are common, such as the full moon or a slice of round fruit. The circle is the basis for the wheel, which, with related inventions such as gears, makes much of modern machinery possible. In mathematics, the study of the circle has helped inspire the development of geometry, astronomy and calculus. Terminology * Annulus: a ring-shaped object, the region bounded by two concentric circles. * Arc: any connected part of a circle. Specifying two end points of an arc and a centre allows for two arcs that together make up ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
American Mathematical Society
The American Mathematical Society (AMS) is an association of professional mathematicians dedicated to the interests of mathematical research and scholarship, and serves the national and international community through its publications, meetings, advocacy and other programs. The society is one of the four parts of the Joint Policy Board for Mathematics and a member of the Conference Board of the Mathematical Sciences. History The AMS was founded in 1888 as the New York Mathematical Society, the brainchild of Thomas Fiske, who was impressed by the London Mathematical Society on a visit to England. John Howard Van Amringe became the first president while Fiske became secretary. The society soon decided to publish a journal, but ran into some resistance over concerns about competing with the '' American Journal of Mathematics''. The result was the ''Bulletin of the American Mathematical Society'', with Fiske as editor-in-chief. The de facto journal, as intended, was influentia ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Apollonius Quadrilateral
In geometry, an Apollonius quadrilateral is a quadrilateral ABCD such that the two products of opposite side lengths are equal. That is, \overline\cdot\overline=\overline\cdot\overline. An equivalent way of stating this definition is that the cross ratio of the four points is \pm 1. It is allowed for the quadrilateral sides to cross. The Apollonius quadrilaterals are important in inversive geometry, because the property of being an Apollonius quadrilateral is preserved by Möbius transformations, and every continuous transformation of the plane that preserves all Apollonius quadrilaterals must be a Möbius transformation. Every kite is an Apollonius quadrilateral. A special case of the Apollonius quadrilaterals are the harmonic quadrilaterals; these are cyclic Apollonius quadrilaterals, inscribed in a given circle. They may be constructed by choosing two opposite vertices A and C arbitrarily on the circle, letting E be any point exterior to the circle on line AC, and setting ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stereographic Projection
In mathematics, a stereographic projection is a perspective transform, perspective projection of the sphere, through a specific point (geometry), point on the sphere (the ''pole'' or ''center of projection''), onto a plane (geometry), plane (the ''projection plane'') perpendicular to the diameter through the point. It is a smooth function, smooth, bijection, bijective function (mathematics), function from the entire sphere except the center of projection to the entire plane. It maps circle of a sphere, circles on the sphere to generalised circle, circles or lines on the plane, and is conformal map, conformal, meaning that it preserves angles at which curves meet and thus Local property, locally approximately preserves similarity (geometry), shapes. It is neither isometry, isometric (distance preserving) nor Equiareal map, equiareal (area preserving). The stereographic projection gives a way to representation (mathematics), represent a sphere by a plane. The metric tensor, metric ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bloch Sphere
In quantum mechanics and computing, the Bloch sphere is a geometrical representation of the pure state space of a two-level quantum mechanical system ( qubit), named after the physicist Felix Bloch. Mathematically each quantum mechanical system is associated with a separable complex Hilbert space H. A pure state of a quantum system is represented by a non-zero vector \psi in H. As the vectors \psi and \lambda \psi (with \lambda \in \mathbb^*) represent the same state, the level of the quantum system corresponds to the dimension of the Hilbert space and pure states can be represented as equivalence classes, or, rays in a projective Hilbert space \mathbf(H_)=\mathbb\mathbf^. For a two-dimensional Hilbert space, the space of all such states is the complex projective line \mathbb\mathbf^1. This is the Bloch sphere, which can be mapped to the Riemann sphere. The Bloch sphere is a unit 2-sphere, with antipodal points corresponding to a pair of mutually orthogonal state vec ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rabi Cycle
In physics, the Rabi cycle (or Rabi flop) is the cyclic behaviour of a two-level quantum system in the presence of an oscillatory driving field. A great variety of physical processes belonging to the areas of quantum computing, condensed matter, atomic and molecular physics, and nuclear and particle physics can be conveniently studied in terms of two-level quantum mechanical systems, and exhibit Rabi flopping when coupled to an optical driving field. The effect is important in quantum optics, magnetic resonance, and quantum computing, and is named after Isidor Isaac Rabi. A two-level system is one that has two possible energy levels. One level is a ground state with lower energy, and the other is an excited state with higher energy. If the energy levels are not degenerate (i.e. don't have equal energies), the system can absorb or emit a quantum of energy and transition from the ground state to the excited state or vice versa. When an atom (or some other two-level system) is illu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polariton
In physics, polaritons are bosonic quasiparticles resulting from strong coupling of electromagnetic waves (photon) with an electric or magnetic dipole-carrying excitation (state) of solid or liquid matter (such as a phonon, plasmon, or an exciton). Polaritons describe the crossing of the dispersion of light with any interacting resonance. They are an expression of level repulsion (quantum phenomenon), also known as the avoided crossing principle. To this extent polaritons can be thought of as the new normal modes of a given material or structure arising from the strong coupling of the bare modes, which are the photon and the dipolar oscillation. Bosonic quasiparticles are distinct from polarons (fermionic quasiparticle), which is an electron plus an attached phonon cloud. Polaritons violate the weak coupling limit and the associated photons do not propagate freely in crystals. Instead, propagation speed depends strongly on the frequency of the photon. Significant exper ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conformal Map
In mathematics, a conformal map is a function (mathematics), function that locally preserves angles, but not necessarily lengths. More formally, let U and V be open subsets of \mathbb^n. A function f:U\to V is called conformal (or angle-preserving) at a point u_0\in U if it preserves angles between directed curves through u_0, as well as preserving orientation. Conformal maps preserve both angles and the shapes of infinitesimally small figures, but not necessarily their size or curvature. The conformal property may be described in terms of the Jacobian matrix and determinant, Jacobian derivative matrix of a coordinate transformation. The transformation is conformal whenever the Jacobian at each point is a positive scalar times a rotation matrix (Orthogonal matrix, orthogonal with determinant one). Some authors define conformality to include orientation-reversing mappings whose Jacobians can be written as any scalar times any orthogonal matrix. For mappings in two dimensions, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polar Coordinates
In mathematics, the polar coordinate system specifies a given point (mathematics), point in a plane (mathematics), plane by using a distance and an angle as its two coordinate system, coordinates. These are *the point's distance from a reference point called the ''pole'', and *the point's direction from the pole relative to the direction of the ''polar axis'', a ray (geometry), ray drawn from the pole. The distance from the pole is called the ''radial coordinate'', ''radial distance'' or simply ''radius'', and the angle is called the ''angular coordinate'', ''polar angle'', or ''azimuth''. The pole is analogous to the origin in a Cartesian coordinate system. Polar coordinates are most appropriate in any context where the phenomenon being considered is inherently tied to direction and length from a center point in a plane, such as spirals. Planar physical systems with bodies moving around a central point, or phenomena originating from a central point, are often simpler and more in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |