|
Church–Rosser Property
In computer science, confluence is a property of rewriting systems, describing which terms in such a system can be rewritten in more than one way, to yield the same result. This article describes the properties in the most abstract setting of an abstract rewriting system. Motivating examples The usual rules of elementary arithmetic form an abstract rewriting system. For example, the expression (11 + 9) × (2 + 4) can be evaluated starting either at the left or at the right parentheses; however, in both cases the same result is eventually obtained. If every arithmetic expression evaluates to the same result regardless of reduction strategy, the arithmetic rewriting system is said to be ground-confluent. Arithmetic rewriting systems may be confluent or only ground-confluent depending on details of the rewriting system. A second, more abstract example is obtained from the following proof of each group element equalling the inverse of its inverse: This proof starts fr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Koblenz Im Buga-Jahr 2011 - Deutsches Eck 01
Koblenz (; Moselle Franconian: ''Kowelenz''), spelled Coblenz before 1926, is a German city on the banks of the Rhine and the Moselle, a multi-nation tributary. Koblenz was established as a Roman military post by Drusus around 8 B.C. Its name originates from the Latin ', meaning "(at the) confluence". The actual confluence is today known as the " German Corner", a symbol of the unification of Germany that features an equestrian statue of Emperor William I. The city celebrated its 2000th anniversary in 1992. It ranks in population behind Mainz and Ludwigshafen am Rhein to be the third-largest city in Rhineland-Palatinate. Its usual-residents' population is 112,000 (as at 2015). Koblenz lies in a narrow flood plain between high hill ranges, some reaching mountainous height, and is served by an express rail and autobahn network. It is part of the populous Rhineland. History Ancient era Around 1000 BC, early fortifications were erected on the Festung Ehrenbreitstein hill on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Closure (mathematics)
In mathematics, a subset of a given set is closed under an operation of the larger set if performing that operation on members of the subset always produces a member of that subset. For example, the natural numbers are closed under addition, but not under subtraction: is not a natural number, although both 1 and 2 are. Similarly, a subset is said to be closed under a ''collection'' of operations if it is closed under each of the operations individually. The closure of a subset is the result of a closure operator applied to the subset. The ''closure'' of a subset under some operations is the smallest subset that is closed under these operations. It is often called the ''span'' (for example linear span) or the ''generated set''. Definitions Let be a set equipped with one or several methods for producing elements of from other elements of . Operations and (partial) multivariate function are examples of such methods. If is a topological space, the limit of a sequence of element ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matsumoto's Theorem (group Theory)
In group theory, Matsumoto's theorem, proved by , gives conditions for two reduced words of a Coxeter group to represent the same element. Statement If two reduced words represent the same element of a Coxeter group, then Matsumoto's theorem states that the first word can be transformed into the second by repeatedly transforming :''xyxy...'' to ''yxyx...'' (or vice versa) where :''xyxy... = yxyx...'' is one of the defining relations of the Coxeter group. Applications Matsumoto's theorem implies that there is a natural map (not a group homomorphism) from a Coxeter group to the corresponding braid group A braid (also referred to as a plait) is a complex structure or pattern formed by interlacing two or more strands of flexible material such as textile yarns, wire, or hair. The simplest and most common version is a flat, solid, three-strande ..., taking any element of the Coxeter group represented by some reduced word in the generators to the same word in the generators of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gröbner Basis
In mathematics, and more specifically in computer algebra, computational algebraic geometry, and computational commutative algebra, a Gröbner basis is a particular kind of generating set of an ideal in a polynomial ring over a field . A Gröbner basis allows many important properties of the ideal and the associated algebraic variety to be deduced easily, such as the dimension and the number of zeros when it is finite. Gröbner basis computation is one of the main practical tools for solving systems of polynomial equations and computing the images of algebraic varieties under projections or rational maps. Gröbner basis computation can be seen as a multivariate, non-linear generalization of both Euclid's algorithm for computing polynomial greatest common divisors, and Gaussian elimination for linear systems. Gröbner bases were introduced in 1965, together with an algorithm to compute them (Buchberger's algorithm), by Bruno Buchberger in his Ph.D. thesis. He named them after h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ideal (ring Theory)
In ring theory, a branch of abstract algebra, an ideal of a ring is a special subset of its elements. Ideals generalize certain subsets of the integers, such as the even numbers or the multiples of 3. Addition and subtraction of even numbers preserves evenness, and multiplying an even number by any integer (even or odd) results in an even number; these closure and absorption properties are the defining properties of an ideal. An ideal can be used to construct a quotient ring in a way similar to how, in group theory, a normal subgroup can be used to construct a quotient group. Among the integers, the ideals correspond one-for-one with the non-negative integers: in this ring, every ideal is a principal ideal consisting of the multiples of a single non-negative number. However, in other rings, the ideals may not correspond directly to the ring elements, and certain properties of integers, when generalized to rings, attach more naturally to the ideals than to the elements of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polynomial
In mathematics, a polynomial is an expression consisting of indeterminates (also called variables) and coefficients, that involves only the operations of addition, subtraction, multiplication, and positive-integer powers of variables. An example of a polynomial of a single indeterminate is . An example with three indeterminates is . Polynomials appear in many areas of mathematics and science. For example, they are used to form polynomial equations, which encode a wide range of problems, from elementary word problems to complicated scientific problems; they are used to define polynomial functions, which appear in settings ranging from basic chemistry and physics to economics and social science; they are used in calculus and numerical analysis to approximate other functions. In advanced mathematics, polynomials are used to construct polynomial rings and algebraic varieties, which are central concepts in algebra and algebraic geometry. Etymology The word ''polynomial'' join ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jan Willem Klop
Jan Willem Klop (born 1945) is a professor of applied logic at Vrije Universiteit in Amsterdam. He holds a Ph.D. in mathematical logic from Utrecht University. Klop is known for his work on the Algebra of Communicating Processes, co-author of ''TeReSe'' and his fixed point combinator : Yk = (L L L L L L L L L L L L L L L L L L L L L L L L L L) where : L = λabcdefghijklmnopqstuvwxyzr. (r (t h i s i s a f i x e d p o i n t c o m b i n a t o r)) Klop became a member of the Royal Netherlands Academy of Arts and Sciences The Royal Netherlands Academy of Arts and Sciences ( nl, Koninklijke Nederlandse Akademie van Wetenschappen, abbreviated: KNAW) is an organization dedicated to the advancement of science and literature in the Netherlands. The academy is housed ... in 2003. Selected publications * * — preceding technical reporFVI 86-03* — preceding technical reporIEICE COMP 88-90* * * * * References External links Jan Willem Klop's homepage* 19 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
If And Only If
In logic and related fields such as mathematics and philosophy, "if and only if" (shortened as "iff") is a biconditional logical connective between statements, where either both statements are true or both are false. The connective is biconditional (a statement of material equivalence), and can be likened to the standard material conditional ("only if", equal to "if ... then") combined with its reverse ("if"); hence the name. The result is that the truth of either one of the connected statements requires the truth of the other (i.e. either both statements are true, or both are false), though it is controversial whether the connective thus defined is properly rendered by the English "if and only if"—with its pre-existing meaning. For example, ''P if and only if Q'' means that ''P'' is true whenever ''Q'' is true, and the only case in which ''P'' is true is if ''Q'' is also true, whereas in the case of ''P if Q'', there could be other scenarios where ''P'' is true and ''Q'' is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
β-reduction
Lambda calculus (also written as ''λ''-calculus) is a formal system in mathematical logic for expressing computation based on function abstraction and application using variable binding and substitution. It is a universal model of computation that can be used to simulate any Turing machine. It was introduced by the mathematician Alonzo Church in the 1930s as part of his research into the foundations of mathematics. Lambda calculus consists of constructing § lambda terms and performing § reduction operations on them. In the simplest form of lambda calculus, terms are built using only the following rules: * x – variable, a character or string representing a parameter or mathematical/logical value. * (\lambda x.M) – abstraction, function definition (M is a lambda term). The variable x becomes bound in the expression. * (M\ N) – application, applying a function M to an argument N. M and N are lambda terms. The reduction operations include: * (\lambda x.M \rightarrow(\lam ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Normal Form (abstract Rewriting)
In abstract rewriting, an object is in normal form if it cannot be rewritten any further, i.e. it is irreducible. Depending on the rewriting system, an object may rewrite to several normal forms or none at all. Many properties of rewriting systems relate to normal forms. Definitions Stated formally, if (''A'',→) is an abstract rewriting system, ''x''∈''A'' is in normal form if no ''y''∈''A'' exists such that ''x''→''y'', i.e. ''x'' is an irreducible term. An object ''a'' is weakly normalizing if there exists at least one particular sequence of rewrites starting from ''a'' that eventually yields a normal form. A rewriting system has the weak normalization property or is ''(weakly) normalizing'' (WN) if every object is weakly normalizing. An object ''a'' is strongly normalizing if every sequence of rewrites starting from ''a'' eventually terminates with a normal form. An abstract rewriting system is ''strongly normalizing'', ''terminating'', ''noetherian'', or has the (stro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
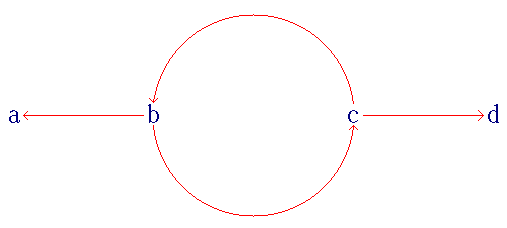
Church–Rosser Theorem
In lambda calculus, the Church–Rosser theorem states that, when applying reduction rules to terms, the ordering in which the reductions are chosen does not make a difference to the eventual result. More precisely, if there are two distinct reductions or sequences of reductions that can be applied to the same term, then there exists a term that is reachable from both results, by applying (possibly empty) sequences of additional reductions. The theorem was proved in 1936 by Alonzo Church and J. Barkley Rosser, after whom it is named. The theorem is symbolized by the adjacent diagram: If term ''a'' can be reduced to both ''b'' and ''c'', then there must be a further term ''d'' (possibly equal to either ''b'' or ''c'') to which both ''b'' and ''c'' can be reduced. Viewing the lambda calculus as an abstract rewriting system, the Church–Rosser theorem states that the reduction rules of the lambda calculus are confluent. As a consequence of the theorem, a term in the lambda calculu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lambda Calculus
Lambda calculus (also written as ''λ''-calculus) is a formal system in mathematical logic for expressing computation based on function abstraction and application using variable binding and substitution. It is a universal model of computation that can be used to simulate any Turing machine. It was introduced by the mathematician Alonzo Church in the 1930s as part of his research into the foundations of mathematics. Lambda calculus consists of constructing § lambda terms and performing § reduction operations on them. In the simplest form of lambda calculus, terms are built using only the following rules: * x – variable, a character or string representing a parameter or mathematical/logical value. * (\lambda x.M) – abstraction, function definition (M is a lambda term). The variable x becomes bound in the expression. * (M\ N) – application, applying a function M to an argument N. M and N are lambda terms. The reduction operations include: * (\lambda x.M \rightarrow(\l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |