|
Chan's Algorithm
In computational geometry, Chan's algorithm, named after Timothy M. Chan, is an optimal output-sensitive algorithm to compute the convex hull of a set P of n points, in 2- or 3-dimensional space. The algorithm takes O(n \log h) time, where h is the number of vertices of the output (the convex hull). In the planar case, the algorithm combines an O(n \log n) algorithm ( Graham scan, for example) with Jarvis march (O(nh)), in order to obtain an optimal O(n \log h) time. Chan's algorithm is notable because it is much simpler than the Kirkpatrick–Seidel algorithm, and it naturally extends to 3-dimensional space. This paradigm has been independently developed by Frank Nielsen in his Ph.D. thesis. Algorithm Overview A single pass of the algorithm requires a parameter m which is between 0 and n (number of points of our set P). Ideally, m = h but h, the number of vertices in the output convex hull, is not known at the start. Multiple passes with increasing values of m are done whi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Gift Wrapping Algorithm
In computational geometry, the gift wrapping algorithm is an algorithm for computing the convex hull of a given set of points. Planar case In the two-dimensional case the algorithm is also known as Jarvis march, after R. A. Jarvis, who published it in 1973; it has O(''nh'') time complexity, where ''n'' is the number of points and ''h'' is the number of points on the convex hull. Its real-life performance compared with other convex hull algorithms is favorable when n is small or h is expected to be very small with respect to n. In general cases, the algorithm is outperformed by many others (see Convex hull algorithms). Algorithm For the sake of simplicity, the description below assumes that the points are in general position, i.e., no three points are collinear. The algorithm may be easily modified to deal with collinearity, including the choice whether it should report only extreme points (vertices of the convex hull) or all points that lie on the convex hull. Also, the compl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Information Processing Letters
''Information Processing Letters'' is a peer review, peer-reviewed scientific journal in the field of computer science, published by Elsevier. The aim of the journal is to enable fast dissemination of results in the field of Data processing, information processing in the form of short papers. Submissions are limited to nine double-spaced pages. The scope of IPL covers fundamental aspects of information processing and computing. This naturally covers topics in the broadly understood field of theoretical computer science, including algorithms, formal languages and automata, computational complexity, computational logic, distributed and parallel algorithms, computational geometry, learning theory, computational number theory, computational biology, coding theory, theoretical cryptography, and applied discrete mathematics. Generally, submissions in all areas of scientific inquiry are considered, provided that they describe research contributions credibly motivated by applications to com ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
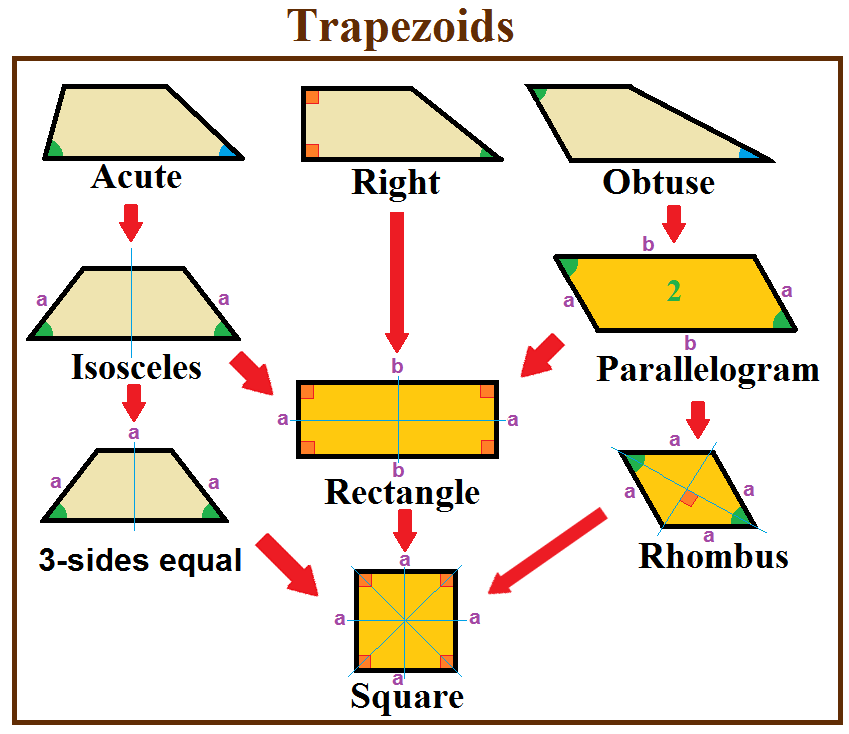
Trapezoid
In geometry, a trapezoid () in North American English, or trapezium () in British English, is a quadrilateral that has at least one pair of parallel sides. The parallel sides are called the ''bases'' of the trapezoid. The other two sides are called the ''legs'' or ''lateral sides''. (If the trapezoid is a parallelogram, then the choice of bases and legs is arbitrary.) A trapezoid is usually considered to be a convex quadrilateral in Euclidean geometry, but there are also crossed cases. If ''ABCD'' is a convex trapezoid, then ''ABDC'' is a crossed trapezoid. The metric formulas in this article apply in convex trapezoids. Definitions ''Trapezoid'' can be defined exclusively or inclusively. Under an exclusive definition a trapezoid is a quadrilateral having pair of parallel sides, with the other pair of opposite sides non-parallel. Parallelograms including rhombi, rectangles, and squares are then not considered to be trapezoids. Under an inclusive definition, a trapezoid is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Lower Envelope
In mathematics, the lower envelope or pointwise minimum of a finite set of functions is the pointwise minimum of the functions, the function whose value at every point is the minimum of the values of the functions in the given set. The concept of a lower envelope can also be extended to partial functions by taking the minimum only among functions that have values at the point. The upper envelope or pointwise maximum is defined symmetrically. For an infinite set of functions, the same notions may be defined using the infimum in place of the minimum, and the supremum in place of the maximum. For continuous functions from a given class, the lower or upper envelope is a piecewise function whose pieces are from the same class. For functions of a single real variable whose graphs have a bounded number of intersection points, the complexity of the lower or upper envelope can be bounded using Davenport–Schinzel sequences, and these envelopes can be computed efficiently by a divide-and-co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Curve Orientation
In mathematics, an orientation of a curve is the choice of one of the two possible directions for travelling on the curve. For example, for Cartesian coordinates, the -axis is traditionally oriented toward the right, and the -axis is upward oriented. In the case of a plane simple closed curve (that is, a curve in the plane whose starting point is also the end point and which has no other self-intersections), the curve is said to be positively oriented or counterclockwise oriented, if one always has the curve interior to the left (and consequently, the curve exterior to the right), when traveling on it. Otherwise, that is if left and right are exchanged, the curve is negatively oriented or clockwise oriented. This definition relies on the fact that every simple closed curve admits a well-defined interior, which follows from the Jordan curve theorem. The inner loop of a beltway road in a country where people drive on the right side of the road is an example of a negatively orie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Gift Wrapping Algorithm
In computational geometry, the gift wrapping algorithm is an algorithm for computing the convex hull of a given set of points. Planar case In the two-dimensional case the algorithm is also known as Jarvis march, after R. A. Jarvis, who published it in 1973; it has O(''nh'') time complexity, where ''n'' is the number of points and ''h'' is the number of points on the convex hull. Its real-life performance compared with other convex hull algorithms is favorable when n is small or h is expected to be very small with respect to n. In general cases, the algorithm is outperformed by many others (see Convex hull algorithms). Algorithm For the sake of simplicity, the description below assumes that the points are in general position, i.e., no three points are collinear. The algorithm may be easily modified to deal with collinearity, including the choice whether it should report only extreme points (vertices of the convex hull) or all points that lie on the convex hull. Also, the compl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Computational Geometry (journal)
''Computational Geometry'', also known as ''Computational Geometry: Theory and Applications'', is a peer-reviewed mathematics journal for research in theoretical and applied computational geometry, its applications, techniques, and design and analysis of geometric algorithms. All aspects of computational geometry are covered, including the numerical, graph theoretical and combinatorial aspects, as well as fundamental problems in various areas of application of computational geometry: in computer graphics, pattern recognition, image processing, robotics, electronic design automation, CAD/CAM, and geographical information systems. The journal was founded in 1991 by Jörg-Rüdiger Sack and Jorge Urrutia.. It is indexed by ''Mathematical Reviews'', Zentralblatt MATH, Science Citation Index, and Current Contents ''Current Contents'' is a rapid alerting service database from Clarivate, formerly the Institute for Scientific Information and Thomson Reuters. It is published online ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Binary Search
In computer science, binary search, also known as half-interval search, logarithmic search, or binary chop, is a search algorithm that finds the position of a target value within a sorted array. Binary search compares the target value to the middle element of the array. If they are not equal, the half in which the target cannot lie is eliminated and the search continues on the remaining half, again taking the middle element to compare to the target value, and repeating this until the target value is found. If the search ends with the remaining half being empty, the target is not in the array. Binary search runs in Time complexity#Logarithmic time, logarithmic time in the Best, worst and average case, worst case, making O(\log n) comparisons, where n is the number of elements in the array. Binary search is faster than linear search except for small arrays. However, the array must be sorted first to be able to apply binary search. There are specialized data structures designed fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
INRIA
The National Institute for Research in Digital Science and Technology (Inria) () is a French national research institution focusing on computer science and applied mathematics. It was created under the name French Institute for Research in Computer Science and Automation (IRIA) () in 1967 at Rocquencourt near Paris, part of Plan Calcul. Its first site was the historical premises of SHAPE (central command of NATO military forces), which is still used as Inria's main headquarters. In 1980, IRIA became INRIA. Since 2011, it has been styled ''Inria''. Inria is a Public Scientific and Technical Research Establishment (EPST) under the double supervision of the French Ministry of National Education, Advanced Instruction and Research and the Ministry of Economy, Finance and Industry. Administrative status Inria has nine research centers distributed across France (in Bordeaux, Grenoble- Inovallée, Lille, Lyon, Nancy, Paris- Rocquencourt, Rennes, Saclay, and Sophia Antipolis) a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Kirkpatrick–Seidel Algorithm
The Kirkpatrick–Seidel algorithm, proposed by its authors as a potential "ultimate planar convex hull algorithm", is an algorithm for computing the convex hull of a set of points in the plane, with \mathcal(n \log h) time complexity, where n is the number of input points and h is the number of points (non dominated or maximal points, as called in some texts) in the hull. Thus, the algorithm is output-sensitive: its running time depends on both the input size and the output size. Another output-sensitive algorithm, the gift wrapping algorithm, was known much earlier, but the Kirkpatrick–Seidel algorithm has an asymptotic running time that is significantly smaller and that always improves on the \mathcal(n \log n) bounds of non-output-sensitive algorithms. The Kirkpatrick–Seidel algorithm is named after its inventors, David G. Kirkpatrick and Raimund Seidel. Although the algorithm is asymptotically optimal, it is not very practical for moderate-sized problems. Algorithm The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |