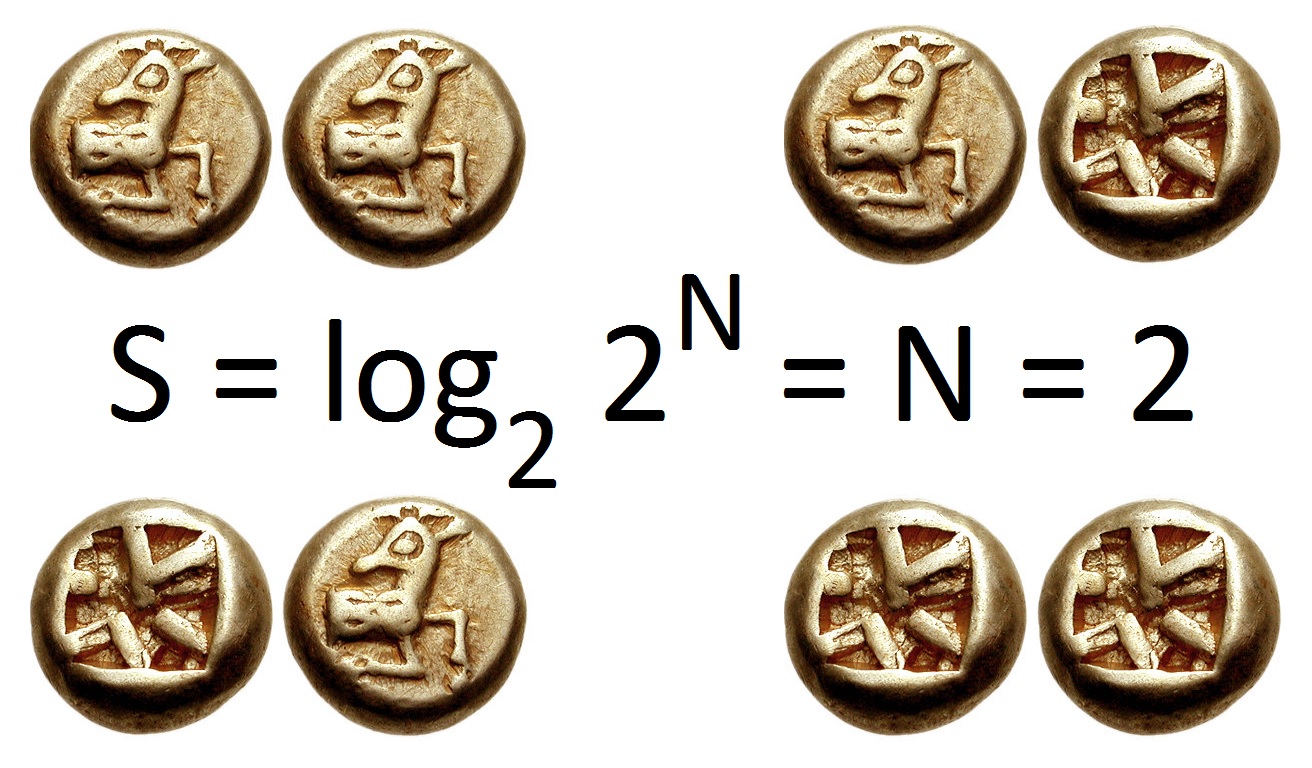|
Chain Rule For Kolmogorov Complexity
The chain rule for Kolmogorov complexity is an analogue of the chain rule for information entropy, which states: : H(X,Y) = H(X) + H(Y, X) That is, the combined randomness of two sequences ''X'' and ''Y'' is the sum of the randomness of ''X'' plus whatever randomness is left in ''Y'' once we know ''X''. This follows immediately from the definitions of conditional and joint entropy, and the fact from probability theory that the joint probability is the product of the marginal and conditional probability: : P(X,Y) = P(X) P(Y, X) : \Rightarrow \log P(X,Y) = \log P(X) + \log P(Y, X) The equivalent statement for Kolmogorov complexity does not hold exactly; it is true only up to a logarithm In mathematics, the logarithm of a number is the exponent by which another fixed value, the base, must be raised to produce that number. For example, the logarithm of to base is , because is to the rd power: . More generally, if , the ...ic term: : K(x,y) = K(x) + K(y, x) + O(\ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kolmogorov Complexity
In algorithmic information theory (a subfield of computer science and mathematics), the Kolmogorov complexity of an object, such as a piece of text, is the length of a shortest computer program (in a predetermined programming language) that produces the object as output. It is a measure of the computational resources needed to specify the object, and is also known as algorithmic complexity, Solomonoff–Kolmogorov–Chaitin complexity, program-size complexity, descriptive complexity, or algorithmic entropy. It is named after Andrey Kolmogorov, who first published on the subject in 1963 and is a generalization of classical information theory. The notion of Kolmogorov complexity can be used to state and prove impossibility results akin to Cantor's diagonal argument, Gödel's incompleteness theorem, and Turing's halting problem. In particular, no program ''P'' computing a lower bound for each text's Kolmogorov complexity can return a value essentially larger than ''P'''s own len ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Big-O Notation
Big ''O'' notation is a mathematical notation that describes the limiting behavior of a function when the argument tends towards a particular value or infinity. Big O is a member of a family of notations invented by German mathematicians Paul Bachmann, Edmund Landau, and others, collectively called Bachmann–Landau notation or asymptotic notation. The letter O was chosen by Bachmann to stand for ''Ordnung'', meaning the order of approximation. In computer science, big O notation is used to classify algorithms according to how their run time or space requirements grow as the input size grows. In analytic number theory, big O notation is often used to express a bound on the difference between an arithmetical function and a better understood approximation; one well-known example is the remainder term in the prime number theorem. Big O notation is also used in many other fields to provide similar estimates. Big O notation characterizes functions according to their growth ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computability Theory
Computability theory, also known as recursion theory, is a branch of mathematical logic, computer science, and the theory of computation that originated in the 1930s with the study of computable functions and Turing degrees. The field has since expanded to include the study of generalized computability and definable set, definability. In these areas, computability theory overlaps with proof theory and effective descriptive set theory. Basic questions addressed by computability theory include: * What does it mean for a function (mathematics), function on the natural numbers to be computable? * How can noncomputable functions be classified into a hierarchy based on their level of noncomputability? Although there is considerable overlap in terms of knowledge and methods, mathematical computability theorists study the theory of relative computability, reducibility notions, and degree structures; those in the computer science field focus on the theory of computational complexity theory ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Information Theory
Information theory is the mathematical study of the quantification (science), quantification, Data storage, storage, and telecommunications, communication of information. The field was established and formalized by Claude Shannon in the 1940s, though early contributions were made in the 1920s through the works of Harry Nyquist and Ralph Hartley. It is at the intersection of electronic engineering, mathematics, statistics, computer science, Neuroscience, neurobiology, physics, and electrical engineering. A key measure in information theory is information entropy, entropy. Entropy quantifies the amount of uncertainty involved in the value of a random variable or the outcome of a random process. For example, identifying the outcome of a Fair coin, fair coin flip (which has two equally likely outcomes) provides less information (lower entropy, less uncertainty) than identifying the outcome from a roll of a dice, die (which has six equally likely outcomes). Some other important measu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Springer-Verlag
Springer Science+Business Media, commonly known as Springer, is a German multinational publishing company of books, e-books and peer-reviewed journals in science, humanities, technical and medical (STM) publishing. Originally founded in 1842 in Berlin, it expanded internationally in the 1960s, and through mergers in the 1990s and a sale to venture capitalists it fused with Wolters Kluwer and eventually became part of Springer Nature in 2015. Springer has major offices in Berlin, Heidelberg, Dordrecht, and New York City. History Julius Springer founded Springer-Verlag in Berlin in 1842 and his son Ferdinand Springer grew it from a small firm of 4 employees into Germany's then second-largest academic publisher with 65 staff in 1872.Chronology ". Springer Science+Business Media. In 1964, Springer expanded its business internationally, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Recursively Enumerable
In computability theory, a set ''S'' of natural numbers is called computably enumerable (c.e.), recursively enumerable (r.e.), semidecidable, partially decidable, listable, provable or Turing-recognizable if: *There is an algorithm such that the set of input numbers for which the algorithm halts is exactly ''S''. Or, equivalently, *There is an algorithm that enumerates the members of ''S''. That means that its output is a list of all the members of ''S'': ''s''1, ''s''2, ''s''3, ... . If ''S'' is infinite, this algorithm will run forever, but each element of S will be returned after a finite amount of time. Note that these elements do not have to be listed in a particular way, say from smallest to largest. The first condition suggests why the term ''semidecidable'' is sometimes used. More precisely, if a number is in the set, one can ''decide'' this by running the algorithm, but if the number is not in the set, the algorithm can run forever, and no information is returned. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mutual Information
In probability theory and information theory, the mutual information (MI) of two random variables is a measure of the mutual Statistical dependence, dependence between the two variables. More specifically, it quantifies the "Information content, amount of information" (in Units of information, units such as shannon (unit), shannons (bits), Nat (unit), nats or Hartley (unit), hartleys) obtained about one random variable by observing the other random variable. The concept of mutual information is intimately linked to that of Entropy (information theory), entropy of a random variable, a fundamental notion in information theory that quantifies the expected "amount of information" held in a random variable. Not limited to real-valued random variables and linear dependence like the Pearson correlation coefficient, correlation coefficient, MI is more general and determines how different the joint distribution of the pair (X,Y) is from the product of the marginal distributions of X and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logarithm
In mathematics, the logarithm of a number is the exponent by which another fixed value, the base, must be raised to produce that number. For example, the logarithm of to base is , because is to the rd power: . More generally, if , then is the logarithm of to base , written , so . As a single-variable function, the logarithm to base is the inverse of exponentiation with base . The logarithm base is called the ''decimal'' or ''common'' logarithm and is commonly used in science and engineering. The ''natural'' logarithm has the number as its base; its use is widespread in mathematics and physics because of its very simple derivative. The ''binary'' logarithm uses base and is widely used in computer science, information theory, music theory, and photography. When the base is unambiguous from the context or irrelevant it is often omitted, and the logarithm is written . Logarithms were introduced by John Napier in 1614 as a means of simplifying calculation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Information Entropy
In information theory, the entropy of a random variable quantifies the average level of uncertainty or information associated with the variable's potential states or possible outcomes. This measures the expected amount of information needed to describe the state of the variable, considering the distribution of probabilities across all potential states. Given a discrete random variable X, which may be any member x within the set \mathcal and is distributed according to p\colon \mathcal\to , 1/math>, the entropy is \Eta(X) := -\sum_ p(x) \log p(x), where \Sigma denotes the sum over the variable's possible values. The choice of base for \log, the logarithm, varies for different applications. Base 2 gives the unit of bits (or " shannons"), while base ''e'' gives "natural units" nat, and base 10 gives units of "dits", "bans", or " hartleys". An equivalent definition of entropy is the expected value of the self-information of a variable. The concept of information entropy was ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conditional Probability
In probability theory, conditional probability is a measure of the probability of an Event (probability theory), event occurring, given that another event (by assumption, presumption, assertion or evidence) is already known to have occurred. This particular method relies on event A occurring with some sort of relationship with another event B. In this situation, the event A can be analyzed by a conditional probability with respect to B. If the event of interest is and the event is known or assumed to have occurred, "the conditional probability of given ", or "the probability of under the condition ", is usually written as or occasionally . This can also be understood as the fraction of probability B that intersects with A, or the ratio of the probabilities of both events happening to the "given" one happening (how many times A occurs rather than not assuming B has occurred): P(A \mid B) = \frac. For example, the probability that any given person has a cough on any given day ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Marginal Probability
In probability theory and statistics, the marginal distribution of a subset of a collection of random variables is the probability distribution of the variables contained in the subset. It gives the probabilities of various values of the variables in the subset without reference to the values of the other variables. This contrasts with a conditional distribution, which gives the probabilities contingent upon the values of the other variables. Marginal variables are those variables in the subset of variables being retained. These concepts are "marginal" because they can be found by summing values in a table along rows or columns, and writing the sum in the margins of the table. The distribution of the marginal variables (the marginal distribution) is obtained by marginalizing (that is, focusing on the sums in the margin) over the distribution of the variables being discarded, and the discarded variables are said to have been marginalized out. The context here is that the theoretic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |