|
Central Projection
In mathematics, a projection is a mapping of a set (or other mathematical structure) into a subset (or sub-structure), which is equal to its square for mapping composition, i.e., which is idempotent. The restriction to a subspace of a projection is also called a ''projection'', even if the idempotence property is lost. An everyday example of a projection is the casting of shadows onto a plane (sheet of paper): the projection of a point is its shadow on the sheet of paper, and the projection (shadow) of a point on the sheet of paper is that point itself (idempotency). The shadow of a three-dimensional sphere is a closed disk. Originally, the notion of projection was introduced in Euclidean geometry to denote the projection of the three-dimensional Euclidean space onto a plane in it, like the shadow example. The two main projections of this kind are: * The projection from a point onto a plane or central projection: If ''C'' is a point, called the center of projection, then th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
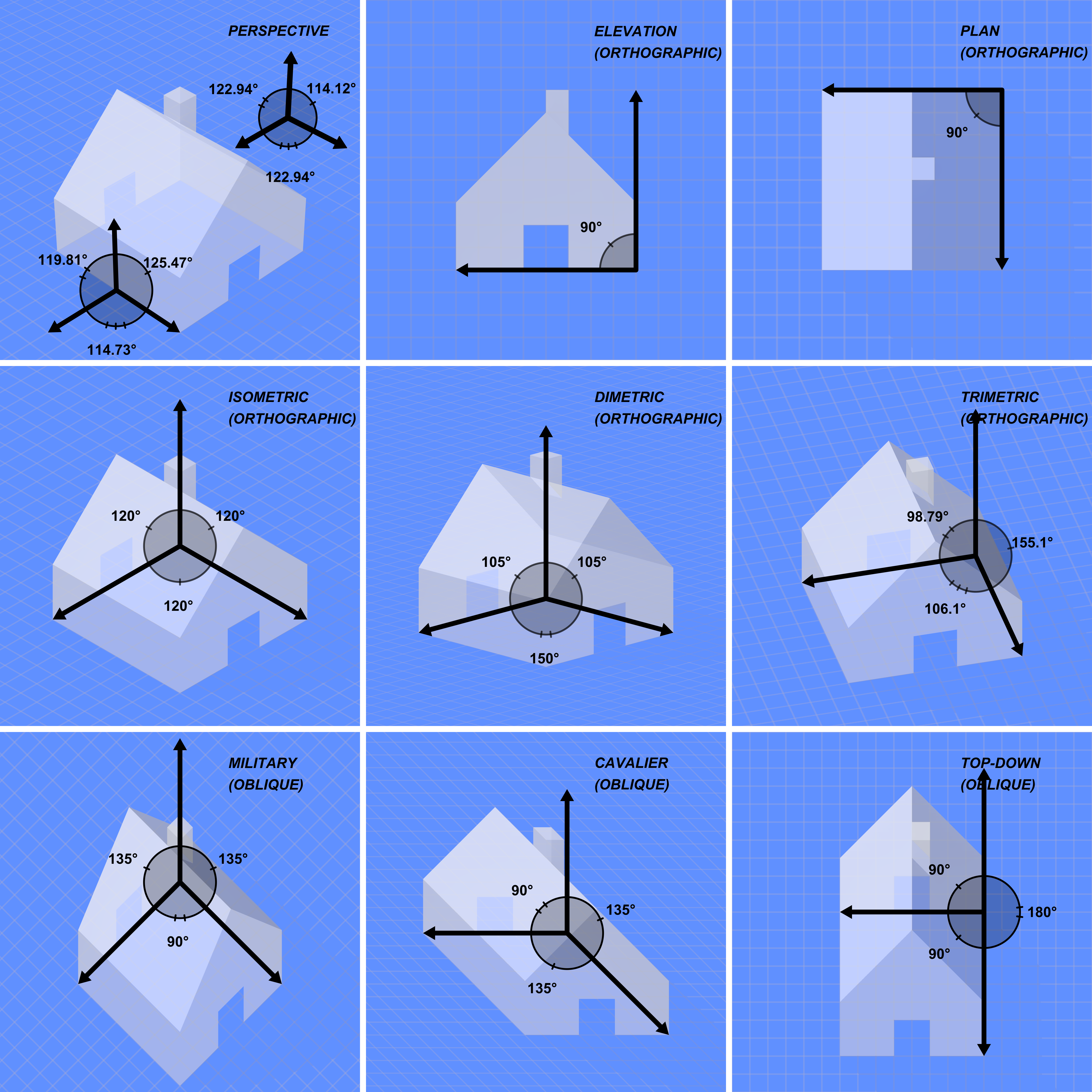
3D Projection
A 3D projection (or graphical projection) is a design technique used to display a three-dimensional (3D) object on a two-dimensional (2D) surface. These projections rely on visual perspective and aspect analysis to project a complex object for viewing capability on a simpler plane. 3D projections use the primary qualities of an object's basic shape to create a map of points, that are then connected to one another to create a visual element. The result is a graphic that contains conceptual properties to interpret that the figure or image as not actually flat (2D), but rather, as a solid object (3D) being viewed on a 2D display. 3D objects are largely displayed on two-dimensional mediums (i.e. paper and computer monitors). As such, graphical projections are a commonly used design element; notably, in engineering drawing, drafting, and computer graphics. Projections can be calculated through employment of mathematical analysis and formulae, or by using various geometric and o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Projection (set Theory)
In set theory, a projection is one of two closely related types of functions or operations, namely: * A set-theoretic operation typified by the ''j''th projection map, written \mathrm_, that takes an element \vec = (x_1,\ \ldots,\ x_j,\ \ldots,\ x_k) of the Cartesian product (X_1 \times \cdots \times X_j \times \cdots \times X_k) to the value \mathrm_(\vec) = x_j. * A function that sends an element ''x'' to its equivalence class under a specified equivalence relation ''E'', or, equivalently, a surjection from a set to another set.. The function from elements to equivalence classes is a surjection, and every surjection corresponds to an equivalence relation under which two elements are equivalent when they have the same image. The result of the mapping is written as 'x''when ''E'' is understood, or written as 'x''sub>''E'' when it is necessary to make ''E'' explicit. See also * Cartesian product * Projection (relational algebra) * Projection (mathematics) * Relation Relation or re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Set Theory
Set theory is the branch of mathematical logic that studies sets, which can be informally described as collections of objects. Although objects of any kind can be collected into a set, set theory, as a branch of mathematics, is mostly concerned with those that are relevant to mathematics as a whole. The modern study of set theory was initiated by the German mathematicians Richard Dedekind and Georg Cantor in the 1870s. In particular, Georg Cantor is commonly considered the founder of set theory. The non-formalized systems investigated during this early stage go under the name of '' naive set theory''. After the discovery of paradoxes within naive set theory (such as Russell's paradox, Cantor's paradox and the Burali-Forti paradox) various axiomatic systems were proposed in the early twentieth century, of which Zermelo–Fraenkel set theory (with or without the axiom of choice) is still the best-known and most studied. Set theory is commonly employed as a foundational ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Injective Function
In mathematics, an injective function (also known as injection, or one-to-one function) is a function that maps distinct elements of its domain to distinct elements; that is, implies . (Equivalently, implies in the equivalent contrapositive statement.) In other words, every element of the function's codomain is the image of one element of its domain. The term must not be confused with that refers to bijective functions, which are functions such that each element in the codomain is an image of exactly one element in the domain. A homomorphism between algebraic structures is a function that is compatible with the operations of the structures. For all common algebraic structures, and, in particular for vector spaces, an is also called a . However, in the more general context of category theory, the definition of a monomorphism differs from that of an injective homomorphism. This is thus a theorem that they are equivalent for algebraic structures; see for more details. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inverse Function
In mathematics, the inverse function of a function (also called the inverse of ) is a function that undoes the operation of . The inverse of exists if and only if is bijective, and if it exists, is denoted by f^ . For a function f\colon X\to Y, its inverse f^\colon Y\to X admits an explicit description: it sends each element y\in Y to the unique element x\in X such that . As an example, consider the real-valued function of a real variable given by . One can think of as the function which multiplies its input by 5 then subtracts 7 from the result. To undo this, one adds 7 to the input, then divides the result by 5. Therefore, the inverse of is the function f^\colon \R\to\R defined by f^(y) = \frac . Definitions Let be a function whose domain is the set , and whose codomain is the set . Then is ''invertible'' if there exists a function from to such that g(f(x))=x for all x\in X and f(g(y))=y for all y\in Y. If is invertible, then there is exactly one function sat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Function Composition
In mathematics, function composition is an operation that takes two functions and , and produces a function such that . In this operation, the function is applied to the result of applying the function to . That is, the functions and are composed to yield a function that maps in domain to in codomain . Intuitively, if is a function of , and is a function of , then is a function of . The resulting ''composite'' function is denoted , defined by for all in . The notation is read as " of ", " after ", " circle ", " round ", " about ", " composed with ", " following ", " then ", or " on ", or "the composition of and ". Intuitively, composing functions is a chaining process in which the output of function feeds the input of function . The composition of functions is a special case of the composition of relations, sometimes also denoted by \circ. As a result, all properties of composition of relations are true of composition of functions, such as the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Codomain
In mathematics, the codomain or set of destination of a function is the set into which all of the output of the function is constrained to fall. It is the set in the notation . The term range is sometimes ambiguously used to refer to either the codomain or image of a function. A codomain is part of a function if is defined as a triple where is called the ''domain'' of , its ''codomain'', and its ''graph''. The set of all elements of the form , where ranges over the elements of the domain , is called the ''image'' of . The image of a function is a subset of its codomain so it might not coincide with it. Namely, a function that is not surjective has elements in its codomain for which the equation does not have a solution. A codomain is not part of a function if is defined as just a graph. For example in set theory it is desirable to permit the domain of a function to be a proper class , in which case there is formally no such thing as a triple . With such a defi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Domain Of A Function
In mathematics, the domain of a function is the set of inputs accepted by the function. It is sometimes denoted by \operatorname(f) or \operatornamef, where is the function. More precisely, given a function f\colon X\to Y, the domain of is . Note that in modern mathematical language, the domain is part of the definition of a function rather than a property of it. In the special case that and are both subsets of \R, the function can be graphed in the Cartesian coordinate system. In this case, the domain is represented on the -axis of the graph, as the projection of the graph of the function onto the -axis. For a function f\colon X\to Y, the set is called the codomain, and the set of values attained by the function (which is a subset of ) is called its range or image. Any function can be restricted to a subset of its domain. The restriction of f \colon X \to Y to A, where A\subseteq X, is written as \left. f \_A \colon A \to Y. Natural domain If a real function is giv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Projective Space
In mathematics, the concept of a projective space originated from the visual effect of perspective, where parallel lines seem to meet ''at infinity''. A projective space may thus be viewed as the extension of a Euclidean space, or, more generally, an affine space with points at infinity, in such a way that there is one point at infinity of each direction of parallel lines. This definition of a projective space has the disadvantage of not being isotropic, having two different sorts of points, which must be considered separately in proofs. Therefore, other definitions are generally preferred. There are two classes of definitions. In synthetic geometry, ''point'' and ''line'' are primitive entities that are related by the incidence relation "a point is on a line" or "a line passes through a point", which is subject to the axioms of projective geometry. For some such set of axioms, the projective spaces that are defined have been shown to be equivalent to those resulting from the fol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bijection
In mathematics, a bijection, also known as a bijective function, one-to-one correspondence, or invertible function, is a function between the elements of two sets, where each element of one set is paired with exactly one element of the other set, and each element of the other set is paired with exactly one element of the first set. There are no unpaired elements. In mathematical terms, a bijective function is a one-to-one (injective) and onto (surjective) mapping of a set ''X'' to a set ''Y''. The term ''one-to-one correspondence'' must not be confused with ''one-to-one function'' (an injective function; see figures). A bijection from the set ''X'' to the set ''Y'' has an inverse function from ''Y'' to ''X''. If ''X'' and ''Y'' are finite sets, then the existence of a bijection means they have the same number of elements. For infinite sets, the picture is more complicated, leading to the concept of cardinal number—a way to distinguish the various sizes of infinite sets. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |