|
Cavalieri's Principle
In geometry, Cavalieri's principle, a modern implementation of the method of indivisibles, named after Bonaventura Cavalieri, is as follows: * 2-dimensional case: Suppose two regions in a plane are included between two parallel lines in that plane. If every line parallel to these two lines intersects both regions in line segments of equal length, then the two regions have equal areas. * 3-dimensional case: Suppose two regions in three-space (solids) are included between two parallel planes. If every plane parallel to these two planes intersects both regions in cross section (geometry), cross-sections of equal area, then the two regions have equal volumes. Today Cavalieri's principle is seen as an early step towards integral calculus, and while it is used in some forms, such as its generalization in Fubini's theorem and layer cake representation, results using Cavalieri's principle can often be shown more directly via integration. In the other direction, Cavalieri's principle gre ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cavalieri Gold
Cavalieri is an Italian language, Italian surname. Notable people with the surname include: * Bonaventura Cavalieri (1598–1647), Italian mathematician * Caterina Cavalieri (1755–1801), Austrian opera soprano * Diego Cavalieri (born 1982), Brazilian footballer; goalkeeper for Crystal Palace F.C. * Emilio de' Cavalieri (1550–1602), Italian composer of the late Renaissance * Grace Cavalieri (born 1932), American poet and playwright * Joey Cavalieri, American comic book writer and editor * Lina Cavalieri (1874–1944), Italian opera soprano * Paola Cavalieri (born 1950), Italian philosopher * Tommaso dei Cavalieri (c. 1508–1587), Italian friend of Michelangelo See also * Cavalieri's principle * Cavalieri's quadrature formula {{surname, Cavalieri Italian-language surnames ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Codimension
In mathematics, codimension is a basic geometric idea that applies to subspaces in vector spaces, to submanifolds in manifolds, and suitable subsets of algebraic varieties. For affine and projective algebraic varieties, the codimension equals the height of the defining ideal. For this reason, the height of an ideal is often called its codimension. The dual concept is relative dimension. Definition Codimension is a ''relative'' concept: it is only defined for one object ''inside'' another. There is no “codimension of a vector space (in isolation)”, only the codimension of a vector ''sub''space. If ''W'' is a linear subspace of a finite-dimensional vector space ''V'', then the codimension of ''W'' in ''V'' is the difference between the dimensions: :\operatorname(W) = \dim(V) - \dim(W). It is the complement of the dimension of ''W,'' in that, with the dimension of ''W,'' it adds up to the dimension of the ambient space ''V:'' :\dim(W) + \operatorname(W) = \dim(V). Simi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pythagorean Theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares on the other two sides. The theorem can be written as an equation relating the lengths of the sides , and the hypotenuse , sometimes called the Pythagorean equation: :a^2 + b^2 = c^2 . The theorem is named for the Ancient Greece, Greek philosopher Pythagoras, born around 570 BC. The theorem has been Mathematical proof, proved numerous times by many different methods – possibly the most for any mathematical theorem. The proofs are diverse, including both Geometry, geometric proofs and Algebra, algebraic proofs, with some dating back thousands of years. When Euclidean space is represented by a Cartesian coordinate system in analytic geometry, Euclidean distance satisfies th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sphere
A sphere (from Ancient Greek, Greek , ) is a surface (mathematics), surface analogous to the circle, a curve. In solid geometry, a sphere is the Locus (mathematics), set of points that are all at the same distance from a given point in three-dimensional space.. That given point is the center (geometry), ''center'' of the sphere, and the distance is the sphere's ''radius''. The earliest known mentions of spheres appear in the work of the Greek mathematics, ancient Greek mathematicians. The sphere is a fundamental surface in many fields of mathematics. Spheres and nearly-spherical shapes also appear in nature and industry. Bubble (physics), Bubbles such as soap bubbles take a spherical shape in equilibrium. The Earth is spherical Earth, often approximated as a sphere in geography, and the celestial sphere is an important concept in astronomy. Manufactured items including pressure vessels and most curved mirrors and lenses are based on spheres. Spheres rolling, roll smoothly in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
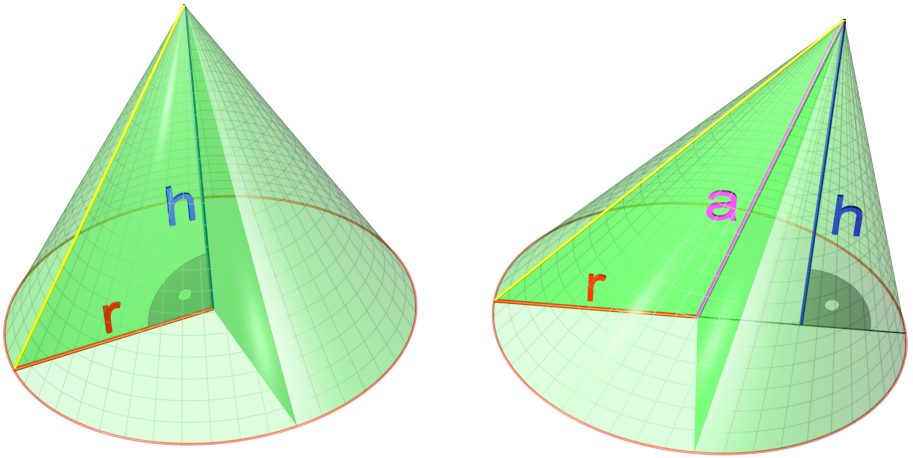
Cone (geometry)
In geometry, a cone is a three-dimensional figure that tapers smoothly from a flat base (typically a circle) to a point not contained in the base, called the '' apex'' or '' vertex''. A cone is formed by a set of line segments, half-lines, or lines connecting a common point, the apex, to all of the points on a base. In the case of line segments, the cone does not extend beyond the base, while in the case of half-lines, it extends infinitely far. In the case of lines, the cone extends infinitely far in both directions from the apex, in which case it is sometimes called a ''double cone''. Each of the two halves of a double cone split at the apex is called a ''nappe''. Depending on the author, the base may be restricted to a circle, any one-dimensional quadratic form in the plane, any closed one-dimensional figure, or any of the above plus all the enclosed points. If the enclosed points are included in the base, the cone is a solid object; otherwise it is an open surface ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sphere Cavalieri
A sphere (from Greek , ) is a surface analogous to the circle, a curve. In solid geometry, a sphere is the set of points that are all at the same distance from a given point in three-dimensional space.. That given point is the ''center'' of the sphere, and the distance is the sphere's ''radius''. The earliest known mentions of spheres appear in the work of the ancient Greek mathematicians. The sphere is a fundamental surface in many fields of mathematics. Spheres and nearly-spherical shapes also appear in nature and industry. Bubbles such as soap bubbles take a spherical shape in equilibrium. The Earth is often approximated as a sphere in geography, and the celestial sphere is an important concept in astronomy. Manufactured items including pressure vessels and most curved mirrors and lenses are based on spheres. Spheres roll smoothly in any direction, so most balls used in sports and toys are spherical, as are ball bearings. Basic terminology As mentioned earlier is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Paraboloid
In geometry, a paraboloid is a quadric surface that has exactly one axial symmetry, axis of symmetry and no central symmetry, center of symmetry. The term "paraboloid" is derived from parabola, which refers to a conic section that has a similar property of symmetry. Every plane section of a paraboloid made by a plane Parallel (geometry)#A line and a plane, parallel to the axis of symmetry is a parabola. The paraboloid is hyperbolic if every other plane section is either a hyperbola, or two crossing lines (in the case of a section by a tangent plane). The paraboloid is elliptic if every other nonempty plane section is either an ellipse, or a single point (in the case of a section by a tangent plane). A paraboloid is either elliptic or hyperbolic. Equivalently, a paraboloid may be defined as a quadric surface that is not a cylinder, and has an implicit surface, implicit equation whose part of degree two may be factored over the complex numbers into two different linear factors. The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hilbert's Third Problem
The third of Hilbert's problems, Hilbert's list of mathematical problems, presented in 1900, was the first to be solved. The problem is related to the following question: given any two polyhedron, polyhedra of equal volume, is it always possible to cut the first into finitely many polyhedral pieces which can be reassembled to yield the second? Based on earlier writings by Carl Friedrich Gauss, David Hilbert conjectured that this is not always possible. This was confirmed within the year by his student Max Dehn, who proved that the answer in general is "no" by producing a counterexample. The answer for the analogous question about polygons in 2 dimensions is "yes" and had been known for a long time; this is the Wallace–Bolyai–Gerwien theorem. Unknown to Hilbert and Dehn, Hilbert's third problem was also proposed independently by Władysław Kretkowski for a math contest of 1882 by the Academy of Arts and Sciences of Kraków, and was solved by Ludwik Birkenmajer, Ludwik Antoni B ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pyramid (geometry)
In geometry, a pyramid is a polyhedron formed by connecting a polygonal base and a point, called the apex (geometry), apex. Each base edge (geometry), edge and apex form a triangle, called a lateral face. A pyramid is a cone, conic solid with a polygonal base. Many types of pyramids can be found by determining the shape of bases, either by based on a regular polygon (regular pyramids) or by cutting off the apex (truncated pyramid). It can be generalized into higher dimensions, known as hyperpyramid. All pyramids are Self-dual polyhedron, self-dual. Etymology The word "pyramid" derives from the ancient Greek term "πυραμίς" (pyramis), which referred to a pyramid-shaped structure and a type of wheat cake. The term is rooted in the Greek "πυρ" (pyr, 'fire') and "άμις" (amis, 'vessel'), highlighting the shape's pointed, flame-like appearance. In Byzantine Greek, the term evolved to "πυραμίδα" (pyramída), continuing to denote pyramid structures. The Greek term " ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Proof Without Words
In mathematics, a proof without words (or visual proof) is an illustration of an identity (mathematics), identity or mathematical statement which can be demonstrated as self-evident by a diagram without any accompanying explanatory text. Such proofs can be considered more Mathematical beauty, elegant than formal or rigour, mathematically rigorous proofs due to their self-evident nature. When the diagram demonstrates a particular case of a general statement, to be a proof, it must be generalisable. A proof without words is not the same as a mathematical proof, because it omits the details of the logical argument it illustrates. However, it can provide valuable intuitions to the viewer that can help them formulate or better understand a true proof. Examples Sum of odd numbers The statement that the sum of all positive parity (mathematics), odd numbers up to 2''n'' − 1 is a square number, perfect square—more specifically, the perfect square ''n''2—can be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Visual Proof Cone Volume
The visual system is the physiological basis of visual perception (the ability to detect and process light). The system detects, transduces and interprets information concerning light within the visible range to construct an image and build a mental model of the surrounding environment. The visual system is associated with the eye and functionally divided into the optical system (including cornea and lens) and the neural system (including the retina and visual cortex). The visual system performs a number of complex tasks based on the ''image forming'' functionality of the eye, including the formation of monocular images, the neural mechanisms underlying stereopsis and assessment of distances to (depth perception) and between objects, motion perception, pattern recognition, accurate motor coordination under visual guidance, and colour vision. Together, these facilitate higher order tasks, such as object identification. The neuropsychological side of visual information proce ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |