|
Cauchy's Theorem (geometry)
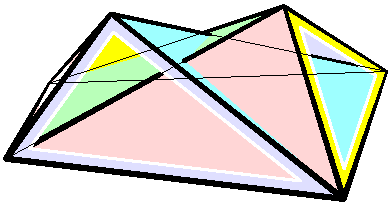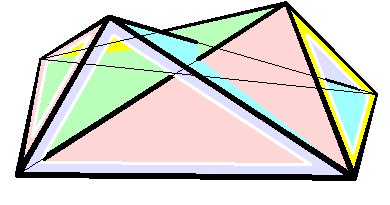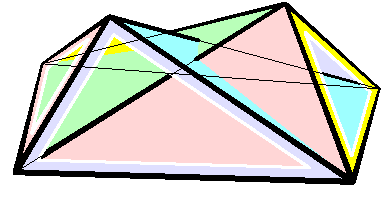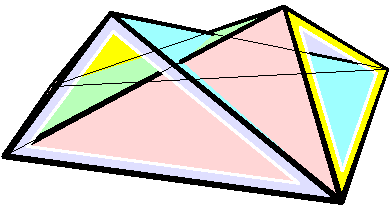
Cauchy's theorem is a theorem in geometry, named after Augustin Cauchy. It states that convex polytopes in three dimensions with congruent corresponding faces must be congruent to each other. That is, any polyhedral net formed by unfolding the faces of the polyhedron onto a flat surface, together with gluing instructions describing which faces should be connected to each other, uniquely determines the shape of the original polyhedron. For instance, if six squares are connected in the pattern of a cube, then they must form a cube: there is no convex polyhedron with six square faces connected in the same way that does not have the same shape. This is a fundamental result in rigidity theory: one consequence of the theorem is that, if one makes a physical model of a convex polyhedron by connecting together rigid plates for each of the polyhedron faces with flexible hinges along the polyhedron edges, then this ensemble of plates and hinges will necessarily form a rigid structure. Stat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is called a ''geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point, line, plane, distance, angle, surface, and curve, as fundamental concepts. During the 19th century several discoveries enlarged dramatically the scope of geometry. One of the oldest such discoveries is Carl Friedrich Gauss' ("remarkable theorem") that asserts roughly that the Gaussian curvature of a surface is independent from any specific embedding in a Euclidean space. This implies that surfaces can be studied ''intrinsically'', that is, as stand-alone spaces, and has been expanded into the theory of manifolds and Riemannian geometry. Later in the 19th century, it appeared that geometries ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bricard Octahedron
In geometry, a Bricard octahedron is a member of a family of flexible polyhedra constructed by Raoul Bricard in 1897. The overall shape of one of these polyhedron may change in a continuous motion, without any changes to the lengths of its edges nor to the shapes of its faces. These octahedra were the first flexible polyhedra to be discovered.. The Bricard octahedra have six vertices, twelve edges, and eight triangular faces, connected in the same way as a regular octahedron. Unlike the regular octahedron, the Bricard octahedra are all non-convex self-crossing polyhedra. By Cauchy's rigidity theorem, a flexible polyhedron must be non-convex, but there exist other flexible polyhedra without self-crossings. Avoiding self-crossings requires more vertices (at least nine) than the six vertices of the Bricard octahedra.. In his publication describing these octahedra, Bricard completely classified the flexible octahedra. His work in this area was later the subject of lectures by Henri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Polyhedra (book)
''Convex Polyhedra'' is a book on the mathematics of convex polyhedra, written by Soviet mathematician Aleksandr Danilovich Aleksandrov, and originally published in Russian in 1950, under the title ''Выпуклые многогранники''. It was translated into German by Wilhelm Süss as ''Konvexe Polyeder'' in 1958. An updated edition, translated into English by Nurlan S. Dairbekov, Semën Samsonovich Kutateladze and Alexei B. Sossinsky, with added material by Victor Zalgaller, L. A. Shor, and Yu. A. Volkov, was published as ''Convex Polyhedra'' by Springer-Verlag in 2005. Topics The main focus of the book is on the specification of geometric data that will determine uniquely the shape of a three-dimensional convex polyhedron, up to some class of geometric transformations such as congruence or similarity. It considers both bounded polyhedra ( convex hulls of finite sets of points) and unbounded polyhedra (intersections of finitely many half-spaces). The 1950 Russian e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Schönhardt Polyhedron
In geometry, the Schönhardt polyhedron is the simplest non-convex polyhedron that cannot be triangulated into tetrahedra without adding new vertices. It is named after German mathematician Erich Schönhardt, who described it in 1928. The same polyhedra have also been studied in connection with Cauchy's rigidity theorem as an example where polyhedra with two different shapes have faces of the same shapes. Construction One way of constructing the Schönhardt polyhedron starts with a triangular prism, with two parallel equilateral triangles as its faces. One of the triangles is rotated around the centerline of the prism, breaking the square faces of the prism into pairs of triangles. If each of these pairs is chosen to be non-convex, the Schönhardt polyhedron is the result. Properties The Schönhardt polyhedron has six vertices, twelve edges, and eight triangular faces. The six vertices of the Schönhardt polyhedron can be used to form fifteen unordered pairs of vertices. Twelv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Aleksei Pogorelov
Aleksei Vasil'evich Pogorelov (russian: Алексе́й Васи́льевич Погоре́лов, ua, Олексі́й Васи́льович Погорє́лов; March 2, 1919 – December 17, 2002), was a Soviet and Ukrainian mathematician. Specialist in the field of convex and differential geometry, geometric PDEs and elastic shells theory, the author of the novel school textbook on geometry and university textbooks on analytical geometry, on differential geometry, and on foundations of geometry. Pogorelov's uniqueness theorem and the Alexandrov–Pogorelov theorem are named after him. Biography Born March 3, 1919 in Korocha, Kursk Governorate (now Belgorod region) in a peasant family. In 1931, because of the collectivization, the parents of Pogorelov escaped from the village to Kharkiv, where his father become a worker at the construction of the Kharkiv tractor plant. In 1935, A.V. Pogorelov won the first prize at the Mathematical Olympiad in Kharkiv S ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stefan Cohn-Vossen
Stefan Cohn-Vossen (28 May 1902 – 25 June 1936) was a mathematician, who was responsible for Cohn-Vossen's inequality and the Cohn-Vossen transformation is also named for him. He proved the first version of the splitting theorem. He was also known for his collaboration with David Hilbert on the 1932 book ''Anschauliche Geometrie'', translated into English language, English as ''Geometry and the Imagination''. He was born in Breslau (then a city in the Kingdom of Prussia; now Wrocław in Poland). He wrote a 1924 doctoral dissertation at the University of Breslau (now the University of Wrocław) under the supervision of Adolf Kneser. He became a professor at the University of Cologne in 1930. He was barred from lecturing in 1933 under Law for the Restoration of the Professional Civil Service, Nazi racial legislation, because he was Jewish.. In 1934 he emigrated to the USSR, with some help from Herman Müntz. While there, he taught at Leningrad University. He died in Moscow fro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geodesic
In geometry, a geodesic () is a curve representing in some sense the shortest path ( arc) between two points in a surface, or more generally in a Riemannian manifold. The term also has meaning in any differentiable manifold with a connection. It is a generalization of the notion of a "straight line". The noun '' geodesic'' and the adjective ''geodetic'' come from ''geodesy'', the science of measuring the size and shape of Earth, though many of the underlying principles can be applied to any ellipsoidal geometry. In the original sense, a geodesic was the shortest route between two points on the Earth's surface. For a spherical Earth, it is a segment of a great circle (see also great-circle distance). The term has since been generalized to more abstract mathematical spaces; for example, in graph theory, one might consider a geodesic between two vertices/nodes of a graph. In a Riemannian manifold or submanifold, geodesics are characterised by the property of having vanishin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Metric Space
In mathematics, a metric space is a set together with a notion of ''distance'' between its elements, usually called points. The distance is measured by a function called a metric or distance function. Metric spaces are the most general setting for studying many of the concepts of mathematical analysis and geometry. The most familiar example of a metric space is 3-dimensional Euclidean space with its usual notion of distance. Other well-known examples are a sphere equipped with the angular distance and the hyperbolic plane. A metric may correspond to a metaphorical, rather than physical, notion of distance: for example, the set of 100-character Unicode strings can be equipped with the Hamming distance, which measures the number of characters that need to be changed to get from one string to another. Since they are very general, metric spaces are a tool used in many different branches of mathematics. Many types of mathematical objects have a natural notion of distance and t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alexandrov's Uniqueness Theorem
The Alexandrov uniqueness theorem is a rigidity theorem in mathematics, describing three-dimensional convex polyhedra in terms of the distances between points on their surfaces. It implies that convex polyhedra with distinct shapes from each other also have distinct metric spaces of surface distances, and it characterizes the metric spaces that come from the surface distances on polyhedra. It is named after Soviet mathematician Aleksandr Danilovich Aleksandrov, who published it in the 1940s. Statement of the theorem The surface of any convex polyhedron in Euclidean space forms a metric space, in which the distance between two points is measured by the length of the shortest path from one point to the other along the surface. Within a single shortest path, distances between pairs of points equal the distances between corresponding points of a line segment of the same length; a path with this property is known as a geodesic. This property of polyhedral surfaces, that every pair ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Max Dehn
Max Wilhelm Dehn (November 13, 1878 – June 27, 1952) was a German mathematician most famous for his work in geometry, topology and geometric group theory. Born to a Jewish family in Germany, Dehn's early life and career took place in Germany. However, he was forced to retire in 1935 and eventually fled Germany in 1939 and emigrated to the United States. Dehn was a student of David Hilbert, and in his habilitation in 1900 Dehn resolved Hilbert's third problem, making him the first to resolve one of Hilbert's well-known 23 problems. Dehn's students include Ott-Heinrich Keller, Ruth Moufang, Wilhelm Magnus, and the artists Dorothea Rockburne and Ruth Asawa. Biography Dehn was born to a family of Jewish origin in Hamburg, Imperial Germany. He studied the foundations of geometry with Hilbert at Göttingen in 1899, and obtained a proof of the Jordan curve theorem for polygons. In 1900 he wrote his dissertation on the role of the Legendre angle sum theorem in axiomatic geome ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Closed Surface
In the part of mathematics referred to as topology, a surface is a two-dimensional manifold. Some surfaces arise as the boundaries of three-dimensional solids; for example, the sphere is the boundary of the solid ball. Other surfaces arise as graphs of functions of two variables; see the figure at right. However, surfaces can also be defined abstractly, without reference to any ambient space. For example, the Klein bottle is a surface that cannot be embedded in three-dimensional Euclidean space. Topological surfaces are sometimes equipped with additional information, such as a Riemannian metric or a complex structure, that connects them to other disciplines within mathematics, such as differential geometry and complex analysis. The various mathematical notions of surface can be used to model surfaces in the physical world. In general In mathematics, a surface is a geometrical shape that resembles a deformed plane. The most familiar examples arise as boundaries of solid o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Simply Connected Space
In topology, a topological space is called simply connected (or 1-connected, or 1-simply connected) if it is path-connected and every path between two points can be continuously transformed (intuitively for embedded spaces, staying within the space) into any other such path while preserving the two endpoints in question. The fundamental group of a topological space is an indicator of the failure for the space to be simply connected: a path-connected topological space is simply connected if and only if its fundamental group is trivial. Definition and equivalent formulations A topological space X is called if it is path-connected and any loop in X defined by f : S^1 \to X can be contracted to a point: there exists a continuous map F : D^2 \to X such that F restricted to S^1 is f. Here, S^1 and D^2 denotes the unit circle and closed unit disk in the Euclidean plane respectively. An equivalent formulation is this: X is simply connected if and only if it is path-connected, and whene ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |