Bricard octahedron

In geometry, a Bricard octahedron is a member of a family of flexible polyhedra constructed by Raoul Bricard in 1897.
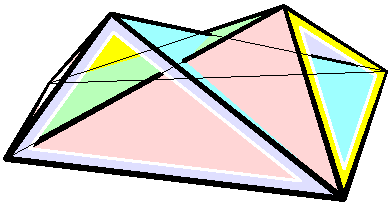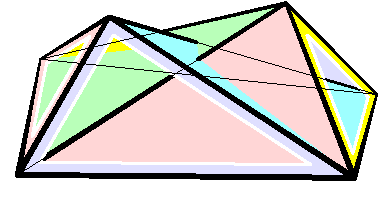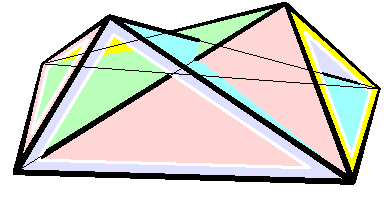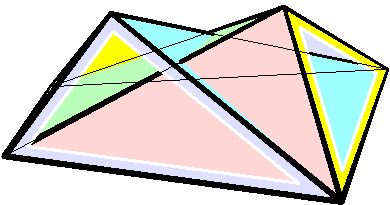
The overall shape of one of these polyhedron may change in a continuous motion, without any changes to the lengths of its edges nor to the shapes of its faces.
These octahedra were the first flexible polyhedra to be discovered..

The Bricard octahedra have six vertices, twelve edges, and eight triangular faces, connected in the same way as a regular octahedron. Unlike the regular octahedron, the Bricard octahedra are all non-convex self-crossing polyhedra. By Cauchy's rigidity theorem, a flexible polyhedron must be non-convex, but there exist other flexible polyhedra without self-crossings. Avoiding self-crossings requires more vertices (at least nine) than the six vertices of the Bricard octahedra..

In his publication describing these octahedra, Bricard completely classified the flexible octahedra. His work in this area was later the subject of lectures by Henri Lebesgue at the Collège de France.

Construction

A Bricard octahedron may be formed from three pairs of points, each symmetric around a common axis of 180° rotational symmetry, with no plane containing all six points. These points form the vertices of the octahedron. The triangular faces of the octahedron have one point from each of the three symmetric pairs. For each pair, there are two ways of choosing one point from the pair, so there are eight triangular faces altogether. The edges of the octahedron are the sides of these triangles, and include one point from each of two symmetric pairs. There are 12 edges, which form the octahedral graph ...

As an example, the six points (0,0,±1), (0,±1,0), and (±1,0,0) form the vertices of a regular octahedron, with each point opposite in the octahedron to its negation, but this is not flexible. Instead, these same six points can be paired up differently to form a Bricard octahedron, with a diagonal axis of symmetry. If this axis is chosen as the line through the origin and the point (0,1,1), then the three symmetric pairs of points for this axis are
(0,0,1)—(0,1,0), (0,0,−1)—(0,−1,0), and (1,0,0)–(−1,0,0). The resulting Bricard octahedron resembles one of the extreme configurations of the second animation, which has an equatorial antiparallelogram.

As a linkage

It is also possible to think of the Bricard octahedron as a mechanical linkage consisting of the twelve edges, connected by flexible joints at the vertices, without the faces. Omitting the faces eliminates the self-crossings for many (but not all) positions of these octahedra. The resulting kinematic chain has one degree of freedom of motion, the same as the polyhedron from which it is derived.

Explanation

The quadrilaterals formed by the edges between the points in any two symmetric pairs of points can be thought of as equators of the octahedron. These equators have the property (by their symmetry) that opposite pairs of quadrilateral sides have equal length. Every quadrilateral with opposite pairs of equal sides, embedded in Euclidean space, has axial symmetry, and some (such as the rectangle) have other symmetries besides. If one cuts the Bricard octahedron into two open-bottomed pyramids by slicing it along one of its equators, both of these open pyramids can flex, and the flexing motion can be made to preserve the axis of symmetry of the whole shape. But, by the symmetries of its construction, the flexing motions of these two open pyramids both move the equator along which they were cut in the same way. Therefore, they can be glued back together into a single flexing motion of the whole octahedron.

The property of having opposite sides of equal length is true of the rectangle, parallelogram, and antiparallelogram, and it is possible to construct Bricard octahedra having any of those flat shapes as their equators.
However, the equator of a Bricard octahedron is not required to lie in a plane; instead, it can be a skew quadrilateral. Even for Bricard octahedra constructed to have a flat equator, the equator generally does not remain flat as the octahedron flexes. However, for some Bricard octahedra, such as the octahedron with an antiparallelogram equator shown in the illustration, the symmetries of the polyhedron cause its equator to remain planar at all times.

Additional properties

The Dehn invariant of any Bricard octahedron remains constant as it undergoes its flexing motion. This same property has been proven for all non-self-crossing flexible polyhedra. However, there exist other self-crossing flexible polyhedra for which the Dehn invariant changes continuously as they flex.

Extensions

It is possible to modify the Bricard polyhedra by adding more faces, in order to move the self-crossing parts of the polyhedron away from each other while still allowing it to flex. The simplest of these modifications is a polyhedron discovered by Klaus Steffen with nine vertices and 14 triangular faces. Steffen's polyhedron is the simplest possible flexible polyhedron without self-crossings.

By connecting together multiple shapes derived from the Bricard octahedron, it is possible to construct horn-shaped rigid origami forms whose shape traces out complicated space curves..

References

{{Mathematics of paper folding

Nonconvex polyhedra
Mathematics of rigidity
Linkages (mechanical)