|
Catalogue Of Triangle Cubics
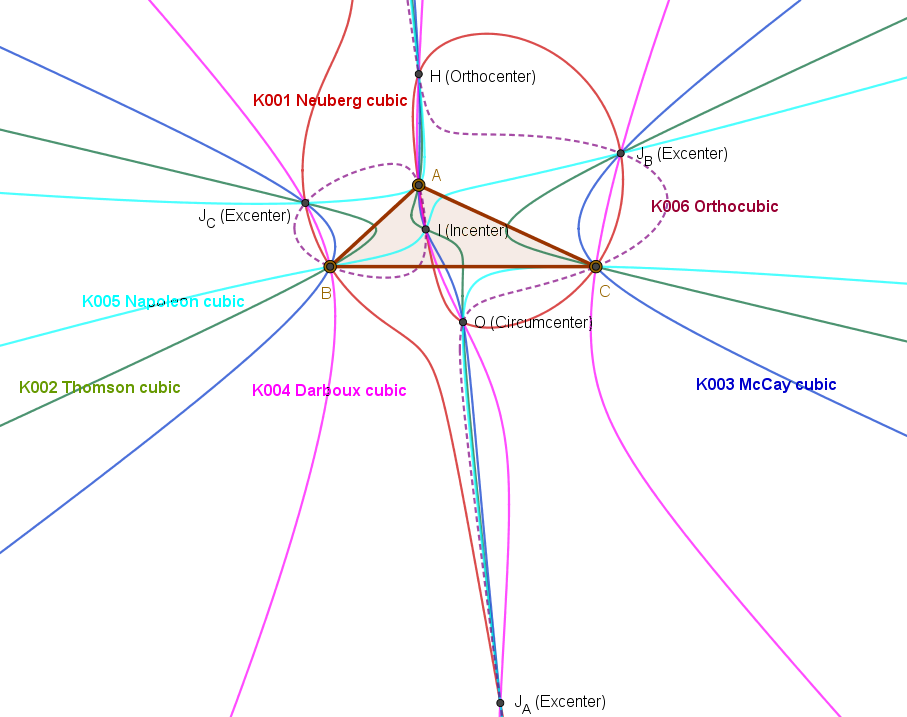
The Catalogue of Triangle Cubics is an online resource containing detailed information about more than 1200 cubic curves in the plane of a reference triangle. The resource is maintained by Bernard Gilbert. Each cubic in the resource is assigned a unique identification number of the form "Knnn" where "nnn" denotes three digits. The identification number of the first entry in the catalogue is "K001" which is the Neuberg cubic of the reference triangle . The catalogue provides, among other things, the following information about each of the cubics listed: * Barycentric equation of the curve *A list of triangle centers which lie on the curve *Special points on the curve which are not triangle centers *Geometric properties of the curve *Locus properties of the curve *Other special properties of the curve *Other curves related to the cubic curve *Plenty of neat and tidy figures illustrating the various properties *References to literature on the curve The equations of some of the cubics ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cubic Plane Curve
In mathematics, a cubic plane curve is a plane algebraic curve defined by a cubic equation : applied to homogeneous coordinates for the projective plane; or the inhomogeneous version for the affine space determined by setting in such an equation. Here is a non-zero linear combination of the third-degree monomials : These are ten in number; therefore the cubic curves form a projective space of dimension 9, over any given field . Each point imposes a single linear condition on , if we ask that pass through . Therefore, we can find some cubic curve through any nine given points, which may be degenerate, and may not be unique, but will be unique and non-degenerate if the points are in general position; compare to two points determining a line and how five points determine a conic. If two cubics pass through a given set of nine points, then in fact a pencil of cubics does, and the points satisfy additional properties; see Cayley–Bacharach theorem. A cubic curve may ha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Neuberg Cubic
In Euclidean geometry, the Neuberg cubic is a special cubic plane curve associated with a reference triangle with several remarkable properties. It is named after Joseph Jean Baptiste Neuberg (30 October 1840 – 22 March 1926), a Luxembourger mathematician, who first introduced the curve in a paper published in 1884. The curve appears as the first item, with identification number K001, in Bernard Gilbert's Catalogue of Triangle Cubics which is a compilation of extensive information about more than 1200 triangle cubics. Definitions The Neuberg cubic can be defined as a locus in many different ways. One way is to define it as a locus of a point in the plane of the reference triangle such that, if the reflections of in the sidelines of triangle are , then the lines are concurrent. However, it needs to be proved that the locus so defined is indeed a cubic curve. A second way is to define it as the locus of point such that if are the circumcenters of triangles , then the lines ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Barycentric Coordinates
In mathematics, an affine space is a geometric structure that generalizes some of the properties of Euclidean spaces in such a way that these are independent of the concepts of distance and measure of angles, keeping only the properties related to parallelism and ratio of lengths for parallel line segments. In an affine space, there is no distinguished point that serves as an origin. Hence, no vector has a fixed origin and no vector can be uniquely associated to a point. In an affine space, there are instead ''displacement vectors'', also called ''translation'' vectors or simply ''translations'', between two points of the space. Thus it makes sense to subtract two points of the space, giving a translation vector, but it does not make sense to add two points of the space. Likewise, it makes sense to add a displacement vector to a point of an affine space, resulting in a new point translated from the starting point by that vector. Any vector space may be viewed as an affine spac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangle Center
In geometry, a triangle center (or triangle centre) is a point in the plane that is in some sense a center of a triangle akin to the centers of squares and circles, that is, a point that is in the middle of the figure by some measure. For example, the centroid, circumcenter, incenter and orthocenter were familiar to the ancient Greeks, and can be obtained by simple constructions. Each of these classical centers has the property that it is invariant (more precisely equivariant) under similarity transformations. In other words, for any triangle and any similarity transformation (such as a rotation, reflection, dilation, or translation), the center of the transformed triangle is the same point as the transformed center of the original triangle. This invariance is the defining property of a triangle center. It rules out other well-known points such as the Brocard points which are not invariant under reflection and so fail to qualify as triangle centers. For an equilateral triangle, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Locus (mathematics)
In geometry, a locus (plural: ''loci'') (Latin word for "place", "location") is a set of all points (commonly, a line, a line segment, a curve or a surface), whose location satisfies or is determined by one or more specified conditions.. In other words, the set of the points that satisfy some property is often called the ''locus of a point'' satisfying this property. The use of the singular in this formulation is a witness that, until the end of the 19th century, mathematicians did not consider infinite sets. Instead of viewing lines and curves as sets of points, they viewed them as places where a point may be ''located'' or may move. History and philosophy Until the beginning of the 20th century, a geometrical shape (for example a curve) was not considered as an infinite set of points; rather, it was considered as an entity on which a point may be located or on which it moves. Thus a circle in the Euclidean plane was defined as the ''locus'' of a point that is at a given dist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thomson Cubic
In geometry, the Thomson cubic of a triangle is the locus of centers of circumconics whose normals at the vertices are concurrent Concurrent means happening at the same time. Concurrency, concurrent, or concurrence may refer to: Law * Concurrence, in jurisprudence, the need to prove both ''actus reus'' and ''mens rea'' * Concurring opinion (also called a "concurrence"), a .... See also * Cubic plane curve – Thomson cubic References *{{mathworld, title=Thomson cubic, urlname=ThomsonCubic * Viktor Vasilʹevich Prasolov: ''Essays on numbers and figures''. AMS, 2000, ISBN 9780821819449, p. 73 External links K002 (Thomson cubic) at Cubics in the Triangle Plane Curves defined for a triangle ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
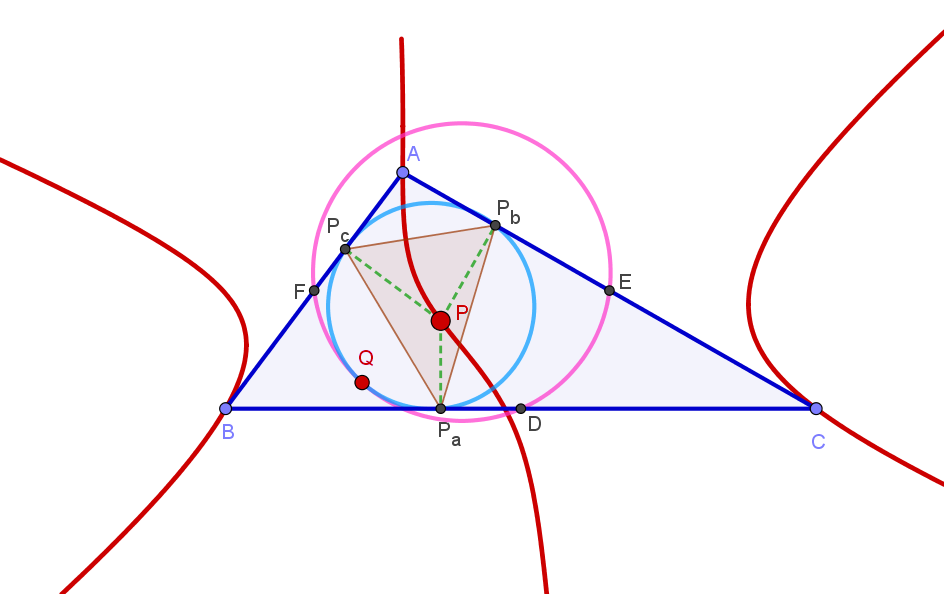
McCay Cubic
In Euclidean geometry, the McCay cubic (also called M'Cay cubic or Griffiths cubic) is a cubic plane curve in the plane of a reference triangle and associated with it. It is the third cubic curve in Bernard Gilbert's Catalogue of Triangle Cubics and it is assigned the identification number K003. Definition The McCay cubic can be defined by locus properties in several ways. For example, the McCay cubic is the locus of a point such that the pedal circle of is tangent to the nine-point circle of the reference triangle . The McCay cubic can also be defined as the locus of point such that the circumcevian triangle of and are orthologic. Equation of the McCay cubic The equation of the McCay cubic in barycentric coordinates x:y:z is :\sum_(a^2(b^2+c^2-a^2)x(c^2y^2-b^2z^2))=0. The equation in trilinear coordinates \alpha : \beta : \gamma is :\alpha (\beta^2 - \gamma^2)\cos A + \beta (\gamma^2 - \alpha^2)\cos B + \gamma (\alpha^2 - \beta^2)\cos C = 0 McCay cubic as a stelloid A ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Darboux Cubic
In mathematics, a cubic plane curve is a plane algebraic curve defined by a cubic equation : applied to homogeneous coordinates for the projective plane; or the inhomogeneous version for the affine space determined by setting in such an equation. Here is a non-zero linear combination of the third-degree monomials : These are ten in number; therefore the cubic curves form a projective space of dimension 9, over any given field . Each point imposes a single linear condition on , if we ask that pass through . Therefore, we can find some cubic curve through any nine given points, which may be degenerate, and may not be unique, but will be unique and non-degenerate if the points are in general position; compare to two points determining a line and how five points determine a conic. If two cubics pass through a given set of nine points, then in fact a pencil of cubics does, and the points satisfy additional properties; see Cayley–Bacharach theorem. A cubic curve may have ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
GeoGebra
GeoGebra (a portmanteau of ''geometry'' and ''algebra'') is an interactive geometry, algebra, statistics and calculus application, intended for learning and teaching mathematics and science from primary school to university level. GeoGebra is available on multiple platforms, with apps for desktops (Windows, macOS and Linux), tablets ( Android, iPad and Windows) and web. History GeoGebra's creator, Markus Hohenwarter, started the project in 2001 as part of his master's thesis at the University of Salzburg. After a successful Kickstarter campaign, GeoGebra expanded its offering to include an iPad, an Android and a Windows Store app version. 2013 GeoGebra incorporated Bernard Parisse's Xcas into its CAS view. The project is now freeware (with open-source portions) and multi-lingual, and Hohenwarter continues to lead its development at the University of Linz. GeoGebra includes both commercial and not-for-profit entities that work together from the head office in Linz, Austria ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Modern Triangle Geometry
In mathematics, modern triangle geometry, or new triangle geometry, is the body of knowledge relating to the properties of a triangle discovered and developed roughly since the beginning of the last quarter of the nineteenth century. Triangles and their properties were the subject of investigation since at least the time of Euclid. In fact, Euclid's '' Elements'' contains description of the four special points – centroid, incenter, circumcenter and orthocenter - associated with a triangle. Even though Pascal and Ceva in the seventeenth century, Euler in the eighteenth century and Feuerbach in the nineteenth century and many other mathematicians had made important discoveries regarding the properties of the triangle, it was the publication in 1873 of a paper by Emile Lemoine (1840–1912) with the title "On a remarkable point of the triangle" that was considered to have, according to Nathan Altschiller-Court, "laid the foundations...of the modern geometry of the triangle as a whole ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |