|
Bundle Adjustment
In photogrammetry and computer stereo vision, bundle adjustment is simultaneous refining of the 3D coordinates describing the scene geometry, the parameters of the relative motion, and the optical characteristics of the camera(s) employed to acquire the images, given a set of images depicting a number of 3D points from different viewpoints. Its name refers to the '' geometrical bundles'' of light rays originating from each 3D feature and converging on each camera's optical center, which are adjusted optimally according to an optimality criterion involving the corresponding image projections of all points. Uses Bundle adjustment is almost always used as the last step of every feature-based 3D reconstruction algorithm. It amounts to an optimization problem on the 3D structure and viewing parameters (i.e., camera pose and possibly intrinsic calibration and radial distortion), to obtain a reconstruction which is optimal under certain assumptions regarding the noise pertaining t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bundle Adjustment Sparse Matrix
Bundle or Bundling may refer to: * Bundling (packaging), the process of using straps to bundle up items Biology * Bundle of His, a collection of heart muscle cells specialized for electrical conduction * Bundle of Kent, an extra conduction pathway between the atria and ventricles in the heart * Hair bundle, a group of cellular processes resembling hair, characteristic of a hair cell Computing * Bundle (OS X), a type of directory in NEXTSTEP and OS X * Bundle (software distribution), a package containing a software and everything it needs to operate * Bundle adjustment, a photogrammetry/computer vision technique Economics * Bundled payment, a method for reimbursing health care providers * Product bundling, a marketing strategy that involves offering several products for sale as one combined product Mathematics and engineering * Bundle (mathematics), a generalization of a fiber bundle dropping the condition of a local product structure * Bundle conductor (power engineering) * Fib ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
System Of Linear Equations
In mathematics, a system of linear equations (or linear system) is a collection of one or more linear equations involving the same variable (math), variables. For example, :\begin 3x+2y-z=1\\ 2x-2y+4z=-2\\ -x+\fracy-z=0 \end is a system of three equations in the three variables . A solution to a linear system is an assignment of values to the variables such that all the equations are simultaneously satisfied. A Equation solving, solution to the system above is given by the Tuple, ordered triple :(x,y,z)=(1,-2,-2), since it makes all three equations valid. The word "system" indicates that the equations are to be considered collectively, rather than individually. In mathematics, the theory of linear systems is the basis and a fundamental part of linear algebra, a subject which is used in most parts of modern mathematics. Computational algorithms for finding the solutions are an important part of numerical linear algebra, and play a prominent role in engineering, physics, chemistry, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geodesy
Geodesy ( ) is the Earth science of accurately measuring and understanding Earth's figure (geometric shape and size), orientation in space, and gravity. The field also incorporates studies of how these properties change over time and equivalent measurements for other planets (known as '' planetary geodesy''). Geodynamical phenomena, including crustal motion, tides and polar motion, can be studied by designing global and national control networks, applying space geodesy and terrestrial geodetic techniques and relying on datums and coordinate systems. The job title is geodesist or geodetic surveyor. History Definition The word geodesy comes from the Ancient Greek word ''geodaisia'' (literally, "division of Earth"). It is primarily concerned with positioning within the temporally varying gravitational field. Geodesy in the German-speaking world is divided into "higher geodesy" ( or ), which is concerned with measuring Earth on the global scale, and "practical geodes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry In Computer Vision
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is called a ''geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point, line, plane, distance, angle, surface, and curve, as fundamental concepts. During the 19th century several discoveries enlarged dramatically the scope of geometry. One of the oldest such discoveries is Carl Friedrich Gauss' ("remarkable theorem") that asserts roughly that the Gaussian curvature of a surface is independent from any specific embedding in a Euclidean space. This implies that surfaces can be studied ''intrinsically'', that is, as stand-alone spaces, and has been expanded into the theory of manifolds and Riemannian geometry. Later in the 19th century, it appeared that geometries wit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ames Stereo Pipeline
The NASA Ames Stereo Pipeline (ASP) is an open-source software package for photogrammetry. It can create digital elevation models and ortho images from stereo planetary data acquired with NASA spacecraft, including for the Moon, Mars, and all other bodies with a solid surface, and also from commercial Earth-orbiting satellites, such as Digital Globe and any vendors who support the RPC camera model, e.g., Pléiades and Cartosat. For stereo correlation ASP uses block-matching and semi-global matching. ASP also provides tools for correcting the input camera poses using bundle adjustment, registration of obtained terrain models using iterative closest point, and a tool for refining a 3D terrain model with shape from shading. ASP integrates the ISIS software for processing planetary data. Binary releases are available for Linux and OSX. See also *Comparison of photogrammetry software *Integrated Software for Imagers and Spectrometers Integrated Software for Imagers and Spectromete ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
MATLAB
MATLAB (an abbreviation of "MATrix LABoratory") is a proprietary multi-paradigm programming language and numeric computing environment developed by MathWorks. MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages. Although MATLAB is intended primarily for numeric computing, an optional toolbox uses the MuPAD symbolic engine allowing access to symbolic computing abilities. An additional package, Simulink, adds graphical multi-domain simulation and model-based design for dynamic and embedded systems. As of 2020, MATLAB has more than 4 million users worldwide. They come from various backgrounds of engineering, science, and economics. History Origins MATLAB was invented by mathematician and computer programmer Cleve Moler. The idea for MATLAB was based on his 1960s PhD thesis. Moler became a math professor at the University of New Mexico and starte ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
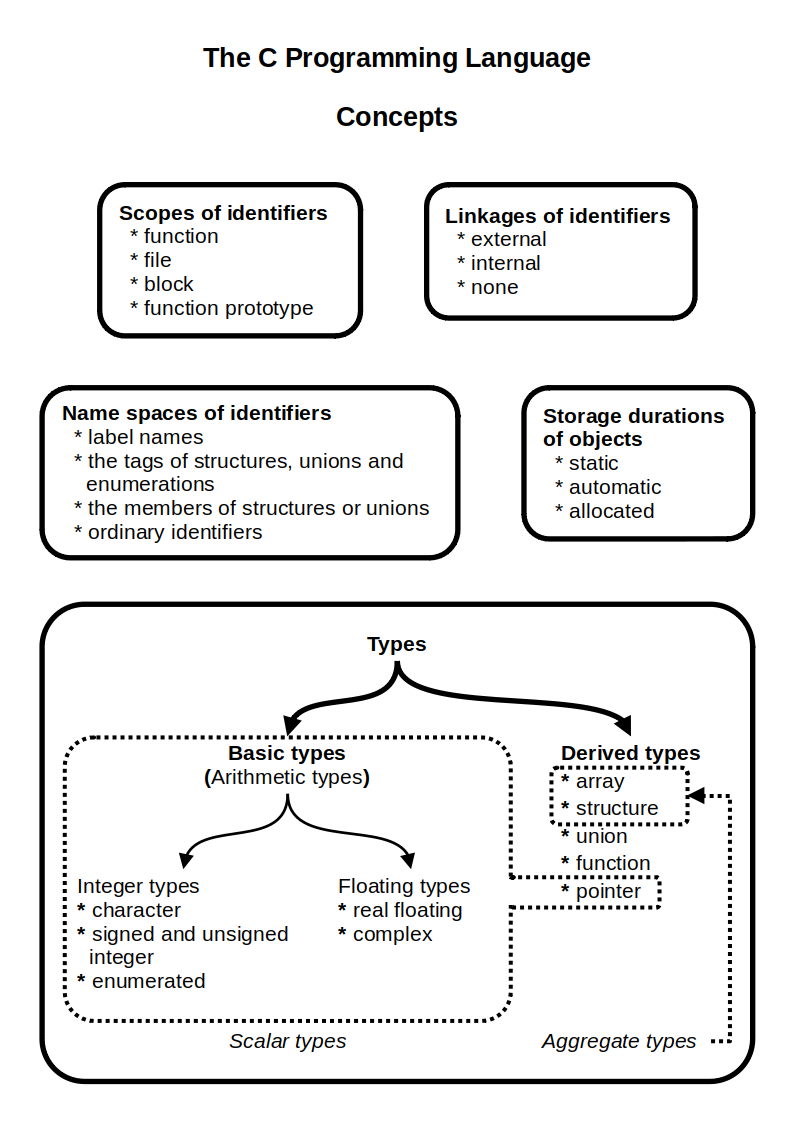
C (programming Language)
C (''pronounced like the letter c'') is a General-purpose language, general-purpose computer programming language. It was created in the 1970s by Dennis Ritchie, and remains very widely used and influential. By design, C's features cleanly reflect the capabilities of the targeted CPUs. It has found lasting use in operating systems, device drivers, protocol stacks, though decreasingly for application software. C is commonly used on computer architectures that range from the largest supercomputers to the smallest microcontrollers and embedded systems. A successor to the programming language B (programming language), B, C was originally developed at Bell Labs by Ritchie between 1972 and 1973 to construct utilities running on Unix. It was applied to re-implementing the kernel of the Unix operating system. During the 1980s, C gradually gained popularity. It has become one of the measuring programming language popularity, most widely used programming languages, with C compilers avail ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Simultaneous Localization And Mapping
Simultaneous localization and mapping (SLAM) is the computational problem of constructing or updating a map of an unknown environment while simultaneously keeping track of an agent's location within it. While this initially appears to be a chicken-and-egg problem, there are several algorithms known for solving it in, at least approximately, tractable time for certain environments. Popular approximate solution methods include the particle filter, extended Kalman filter, covariance intersection, and GraphSLAM. SLAM algorithms are based on concepts in computational geometry and computer vision, and are used in robot navigation, robotic mapping and odometry for virtual reality or augmented reality. SLAM algorithms are tailored to the available resources and are not aimed at perfection but at operational compliance. Published approaches are employed in self-driving cars, unmanned aerial vehicles, autonomous underwater vehicles, planetary rovers, newer domestic robots and even inside ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Structure From Motion
Structure from motion (SfM) is a photogrammetric range imaging technique for estimating three-dimensional structures from two-dimensional image sequences that may be coupled with local motion signals. It is studied in the fields of computer vision and visual perception. In biological vision, SfM refers to the phenomenon by which humans (and other living creatures) can recover 3D structure from the projected 2D (retinal) motion field of a moving object or scene. Principle Humans perceive a great deal of information about the three-dimensional structure in their environment by moving around it. When the observer moves, objects around them move different amounts depending on their distance from the observer. This is known as motion parallax, and from this depth information can be used to generate an accurate 3D representation of the world around them. Finding structure from motion presents a similar problem to finding structure from stereo vision. In both instances, the correspo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Collinearity Equation
The collinearity equations are a set of two equations, used in photogrammetry and computer stereo vision, to relate coordinates in a sensor plane (in two dimensions) to object coordinates (in three dimensions). The equations originate from the central projection of a point of the object through the optical centre of the camera to the image on the sensor plane. Definition Let x,y, and z refer to a coordinate system with the x- and y-axis in the sensor plane. Denote the coordinates of the point P on the object by x_P,y_P,z_P, the coordinates of the image point of P on the sensor plane by ''x'' and ''y'' and the coordinates of the projection (optical) centre by x_0,y_0,z_0. As a consequence of the projection method there is the same fixed ratio \lambda between x-x_0 and x_0-x_P, y-y_0 and y_0-y_P, and the distance of the projection centre to the sensor plane z_0=c and z_P-z_0. Hence: :x-x_0=-\lambda (x_P-x_0) :y-y_0=-\lambda (y_P-y_0) :c=\lambda (z_P-z_0), Solving for \l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stereoscopy
Stereoscopy (also called stereoscopics, or stereo imaging) is a technique for creating or enhancing the illusion of depth in an image by means of stereopsis for binocular vision. The word ''stereoscopy'' derives . Any stereoscopic image is called a stereogram. Originally, stereogram referred to a pair of stereo images which could be viewed using a stereoscope. Most stereoscopic methods present a pair of two-dimensional images to the viewer. The left image is presented to the left eye and the right image is presented to the right eye. When viewed, the human brain perceives the images as a single 3D view, giving the viewer the perception of 3D depth. However, the 3D effect lacks proper focal depth, which gives rise to the Vergence-Accommodation Conflict. Stereoscopy is distinguished from other types of 3D displays that display an image in three full dimensions, allowing the observer to increase information about the 3-dimensional objects being displayed by head and eye mov ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Adjustment Of Observations
Least-squares adjustment is a model for the solution of an overdetermined system of equations based on the principle of least squares of observation residuals. It is used extensively in the disciplines of surveying, geodesy, and photogrammetry—the field of geomatics, collectively. Formulation There are three forms of least squares adjustment: ''parametric'', ''conditional'', and ''combined'': * In parametric adjustment, one can find an observation equation ''h(X)=Y'' relating observations ''Y'' explicitly in terms of parameters ''X'' (leading to the A-model below). * In conditional adjustment, there exists a condition equation which is ''g(Y)=0'' involving only observations ''Y'' (leading to the B-model below) — with no parameters ''X'' at all. * Finally, in a combined adjustment, both parameters ''X'' and observations ''Y'' are involved implicitly in a mixed-model equation ''f(X,Y)=0''. Clearly, parametric and conditional adjustments correspond to the more general combined case ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
