|
Brunt–Väisälä Frequency
In atmospheric dynamics, oceanography, asteroseismology and geophysics, the Brunt–Väisälä frequency, or buoyancy frequency, is a measure of the stability of a fluid to vertical displacements such as those caused by convection. More precisely it is the frequency at which a vertically displaced parcel will oscillate within a statically stable environment. It is named after David Brunt and Vilho Väisälä. It can be used as a measure of atmospheric stratification. Derivation for a general fluid Consider a parcel of water or gas that has density \rho_0. This parcel is in an environment of other water or gas particles where the density of the environment is a function of height: \rho = \rho (z). If the parcel is displaced by a small vertical increment z', ''and it maintains its original density, so that its volume does not change,'' it will be subject to an extra gravitational force against its surroundings of: :\rho_0 \frac = - g \left[\rho (z)-\rho (z+z')\right] where g is the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Atmospheric Dynamics
Meteorology is a branch of the atmospheric sciences (which include atmospheric chemistry and physics) with a major focus on weather forecasting. The study of meteorology dates back millennia, though significant progress in meteorology did not begin until the 18th century. The 19th century saw modest progress in the field after weather observation networks were formed across broad regions. Prior attempts at prediction of weather depended on historical data. It was not until after the elucidation of the laws of physics, and more particularly in the latter half of the 20th century the development of the computer (allowing for the automated solution of a great many modelling equations) that significant breakthroughs in weather forecasting were achieved. An important branch of weather forecasting is marine weather forecasting as it relates to maritime and coastal safety, in which weather effects also include atmospheric interactions with large bodies of water. Meteorological phenom ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ideal Gas Law
The ideal gas law, also called the general gas equation, is the equation of state of a hypothetical ideal gas. It is a good approximation of the behavior of many gases under many conditions, although it has several limitations. It was first stated by Benoît Paul Émile Clapeyron in 1834 as a combination of the empirical Boyle's law, Charles's law, Avogadro's law, and Gay-Lussac's law. The ideal gas law is often written in an empirical form: pV = nRT where p, V and T are the pressure, volume and temperature; n is the amount of substance; and R is the ideal gas constant. It can also be derived from the microscopic kinetic theory, as was achieved (apparently independently) by August Krönig in 1856 and Rudolf Clausius in 1857. Equation The state of an amount of gas is determined by its pressure, volume, and temperature. The modern form of the equation relates these simply in two main forms. The temperature used in the equation of state is an absolute temperature: the appropria ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fluid Dynamics
In physics and engineering, fluid dynamics is a subdiscipline of fluid mechanics that describes the flow of fluids— liquids and gases. It has several subdisciplines, including ''aerodynamics'' (the study of air and other gases in motion) and hydrodynamics (the study of liquids in motion). Fluid dynamics has a wide range of applications, including calculating forces and moments on aircraft, determining the mass flow rate of petroleum through pipelines, predicting weather patterns, understanding nebulae in interstellar space and modelling fission weapon detonation. Fluid dynamics offers a systematic structure—which underlies these practical disciplines—that embraces empirical and semi-empirical laws derived from flow measurement and used to solve practical problems. The solution to a fluid dynamics problem typically involves the calculation of various properties of the fluid, such as flow velocity, pressure, density, and temperature, as functions of space and time. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Atmospheric Dynamics
Meteorology is a branch of the atmospheric sciences (which include atmospheric chemistry and physics) with a major focus on weather forecasting. The study of meteorology dates back millennia, though significant progress in meteorology did not begin until the 18th century. The 19th century saw modest progress in the field after weather observation networks were formed across broad regions. Prior attempts at prediction of weather depended on historical data. It was not until after the elucidation of the laws of physics, and more particularly in the latter half of the 20th century the development of the computer (allowing for the automated solution of a great many modelling equations) that significant breakthroughs in weather forecasting were achieved. An important branch of weather forecasting is marine weather forecasting as it relates to maritime and coastal safety, in which weather effects also include atmospheric interactions with large bodies of water. Meteorological phenom ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Atmospheric Thermodynamics
Atmospheric thermodynamics is the study of heat-to-work transformations (and their reverse) that take place in the earth's atmosphere and manifest as weather or climate. Atmospheric thermodynamics use the laws of classical thermodynamics, to describe and explain such phenomena as the properties of moist air, the formation of clouds, atmospheric convection, boundary layer meteorology, and vertical instabilities in the atmosphere. Atmospheric thermodynamic diagrams are used as tools in the forecasting of storm development. Atmospheric thermodynamics forms a basis for cloud microphysics and convection parameterizations used in numerical weather models and is used in many climate considerations, including convective-equilibrium climate models. Overview The atmosphere is an example of a non-equilibrium system. Atmospheric thermodynamics describes the effect of buoyant forces that cause the rise of less dense (warmer) air, the descent of more dense air, and the transformation of water ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bénard Cell
Benard or Bénard is a surname or given name. Notable people with the name include: Surname * Abraham-Joseph Bénard (1750–1822), French actor of the Comédie-Française * Aimé Bénard (1873–1938), Canadian politician * Alexander Benard, American businessman * André Bénard (1922–2016), French industrialist * Anne-José Madeleine Henriette Bénard (1928–2010), better known as Cécile Aubry, French actress * Catherine Éléonore Bénard (1740–1769), French lady-in-waiting * Cheryl Benard (born 1953), American academic * Chris Benard (born 1990), American track and field athlete * Claude Bénard (born 1926), French athlete * Dominique Bénard, French Deputy Secretary-General of the World Organization of the Scout Movement * Émile Bénard (1844–1929), French architect and painter * Henri Bénard (1874–1939), French physicist, best known for his research on convection * Laurent Bénard (1573–1620), French chief founder of the Maurist Congregation * Marcos Abel ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Buoyancy
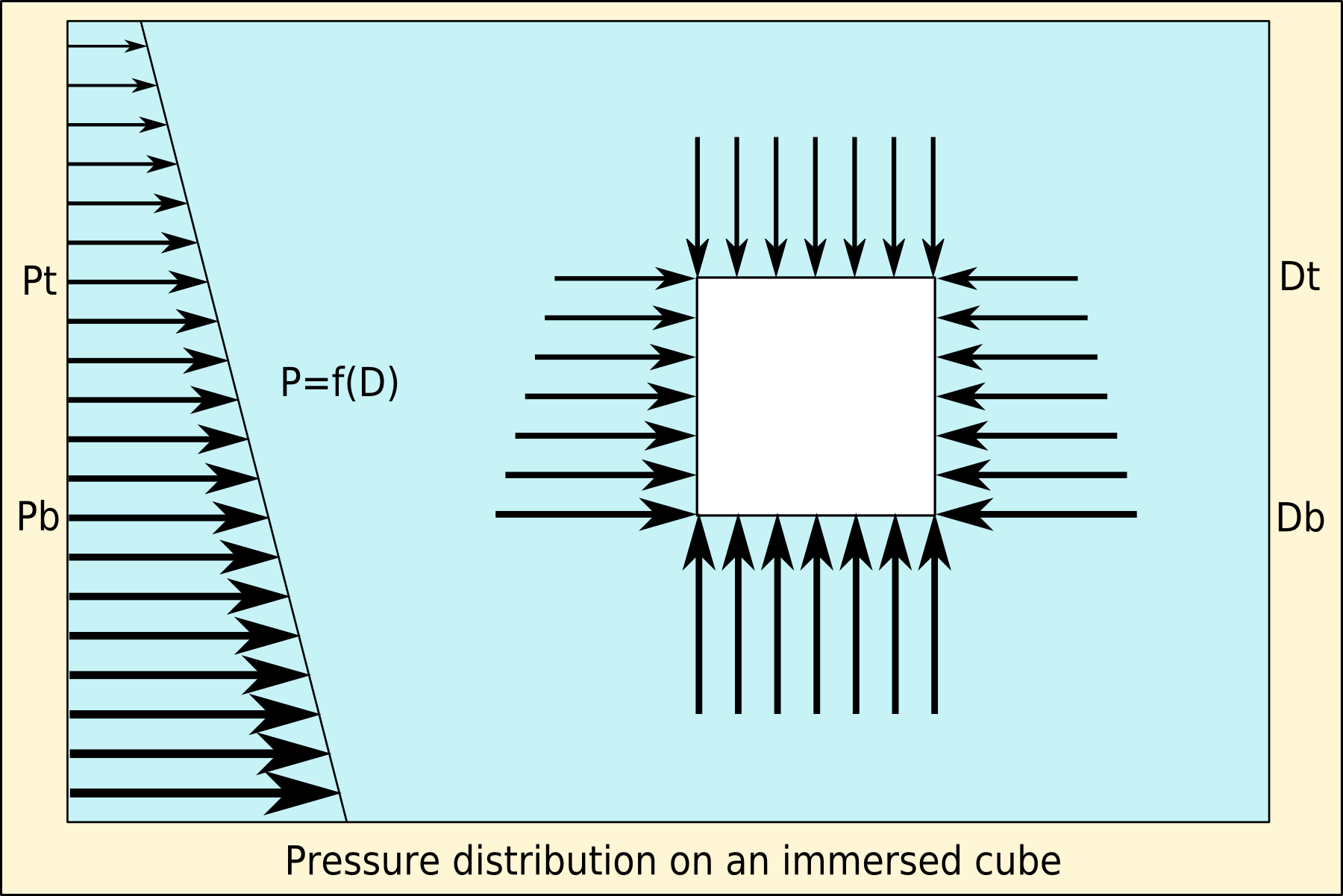
Buoyancy (), or upthrust, is an upward force exerted by a fluid that opposes the weight of a partially or fully immersed object. In a column of fluid, pressure increases with depth as a result of the weight of the overlying fluid. Thus the pressure at the bottom of a column of fluid is greater than at the top of the column. Similarly, the pressure at the bottom of an object submerged in a fluid is greater than at the top of the object. The pressure difference results in a net upward force on the object. The magnitude of the force is proportional to the pressure difference, and (as explained by Archimedes' principle) is equivalent to the weight of the fluid that would otherwise occupy the submerged volume of the object, i.e. the displaced fluid. For this reason, an object whose average density is greater than that of the fluid in which it is submerged tends to sink. If the object is less dense than the liquid, the force can keep the object afloat. This can occur only in a no ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Internal Gravity Waves
Internal waves are gravity waves that oscillate within a fluid medium, rather than on its surface. To exist, the fluid must be stratified: the density must change (continuously or discontinuously) with depth/height due to changes, for example, in temperature and/or salinity. If the density changes over a small vertical distance (as in the case of the thermocline in lakes and oceans or an atmospheric inversion), the waves propagate horizontally like surface waves, but do so at slower speeds as determined by the density difference of the fluid below and above the interface. If the density changes continuously, the waves can propagate vertically as well as horizontally through the fluid. Internal waves, also called internal gravity waves, go by many other names depending upon the fluid stratification, generation mechanism, amplitude, and influence of external forces. If propagating horizontally along an interface where the density rapidly decreases with height, they are specifically ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angular Frequency
In physics, angular frequency "''ω''" (also referred to by the terms angular speed, circular frequency, orbital frequency, radian frequency, and pulsatance) is a scalar measure of rotation rate. It refers to the angular displacement per unit time (for example, in rotation) or the rate of change of the phase of a sinusoidal waveform (for example, in oscillations and waves), or as the rate of change of the argument of the sine function. Angular frequency (or angular speed) is the magnitude of the pseudovector quantity angular velocity.(UP1) One turn is equal to 2''π'' radians, hence \omega = \frac = , where: *''ω'' is the angular frequency (unit: radians per second), *''T'' is the period (unit: seconds), *''f'' is the ordinary frequency (unit: hertz) (sometimes ''ν''). Units In SI units, angular frequency is normally presented in radians per second, even when it does not express a rotational value. The unit hertz (Hz) is dimensionally equivalent, but by convention it ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Potential Density
The potential density of a fluid parcel at pressure P is the density that the parcel would acquire if adiabatically brought to a reference pressure P_, often 1 bar (100 kPa). Whereas density changes with changing pressure, potential density of a fluid parcel is conserved as the pressure experienced by the parcel changes (provided no mixing with other parcels or net heat flux occurs). The concept is used in oceanography and (to a lesser extent) atmospheric science. Potential density is a dynamically important property: for static stability potential density must decrease upward. If it doesn't, a fluid parcel displaced upward finds itself lighter than its neighbors, and continues to move upward; similarly, a fluid parcel displaced downward would be heavier than its neighbors. This is true even if the density of the fluid decreases upward. In stable conditions (potential density decreasing upward) motion along surfaces of constant potential density (isopycnals) is energetically fa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Salinity
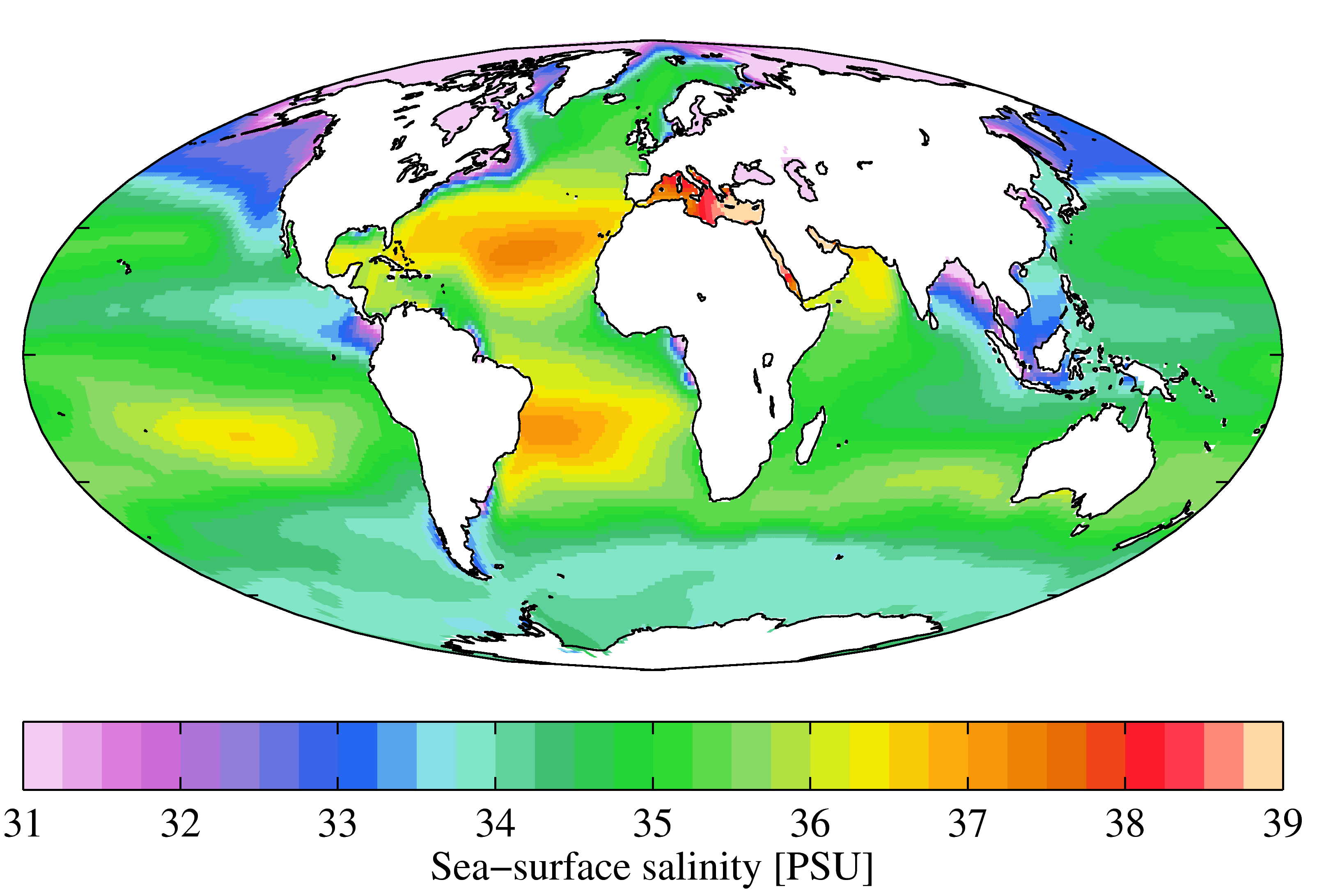
Salinity () is the saltiness or amount of salt dissolved in a body of water, called saline water (see also soil salinity). It is usually measured in g/L or g/kg (grams of salt per liter/kilogram of water; the latter is dimensionless and equal to ‰). Salinity is an important factor in determining many aspects of the chemistry of natural waters and of biological processes within it, and is a thermodynamic state variable that, along with temperature and pressure, governs physical characteristics like the density and heat capacity of the water. A contour line of constant salinity is called an ''isohaline'', or sometimes ''isohale''. Definitions Salinity in rivers, lakes, and the ocean is conceptually simple, but technically challenging to define and measure precisely. Conceptually the salinity is the quantity of dissolved salt content of the water. Salts are compounds like sodium chloride, magnesium sulfate, potassium nitrate, and sodium bicarbonate which dissolve into ions ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Paul Ledoux
Paul Ledoux (8 August 1914 – 6 October 1988) was a Belgian astrophysicist best known for his work on stellar stability and variability. With Theodore Walraven, he co-authored a seminal work on stellar oscillations. In 1964 Ledoux was awarded the Francqui Prize for Exact Sciences, and was awarded the Eddington Medal of the Royal Astronomical Society in 1972 for investigations into problems of stellar stability and variable stars. He was awarded the Janssen Medal of the French Academy of Sciences in 1976. Ledoux criterion In stellar astrophysics, Ledoux's name is now associated with the criterion under which material in a star becomes unstable to convection in the presence of a gradient of chemical composition. In homogeneous material, the Schwarzschild criterion Discovered by Karl Schwarzschild,Karl Schwarzschild, Gesammelte Werke: Collected Works, Page 14, the Schwarzschild criterion is a criterion in astrophysics where a stellar medium is stable against convecti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |