|
Bogoliubov Transformation
In theoretical physics, the Bogoliubov transformation, also known as the Bogoliubov–Valatin transformation, was independently developed in 1958 by Nikolay Bogolyubov and John George Valatin for finding solutions of BCS theory in a homogeneous system. The Bogoliubov transformation is an isomorphism of either the canonical commutation relation algebra or canonical anticommutation relation algebra. This induces an autoequivalence on the respective representations. The Bogoliubov transformation is often used to diagonalize Hamiltonians, which yields the stationary solutions of the corresponding Schrödinger equation. The Bogoliubov transformation is also important for understanding the Unruh effect, Hawking radiation, pairing effects in nuclear physics, and many other topics. The Bogoliubov transformation is often used to diagonalize Hamiltonians, ''with'' a corresponding transformation of the state function. Operator eigenvalues calculated with the diagonalized Hamiltonian on the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Theoretical Physics
Theoretical physics is a branch of physics that employs mathematical models and abstractions of physical objects and systems to rationalize, explain and predict natural phenomena. This is in contrast to experimental physics, which uses experimental tools to probe these phenomena. The advancement of science generally depends on the interplay between experimental studies and theory. In some cases, theoretical physics adheres to standards of mathematical rigour while giving little weight to experiments and observations.There is some debate as to whether or not theoretical physics uses mathematics to build intuition and illustrativeness to extract physical insight (especially when normal experience fails), rather than as a tool in formalizing theories. This links to the question of it using mathematics in a less formally rigorous, and more intuitive or heuristic way than, say, mathematical physics. For example, while developing special relativity, Albert Einstein was concerned wit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Symplectic Vector Space
In mathematics, a symplectic vector space is a vector space ''V'' over a field ''F'' (for example the real numbers R) equipped with a symplectic bilinear form. A symplectic bilinear form is a mapping that is ; Bilinear: Linear in each argument separately; ; Alternating: holds for all ; and ; Non-degenerate: for all implies that . If the underlying field has characteristic not 2, alternation is equivalent to skew-symmetry. If the characteristic is 2, the skew-symmetry is implied by, but does not imply alternation. In this case every symplectic form is a symmetric form, but not vice versa. Working in a fixed basis, ''ω'' can be represented by a matrix. The conditions above are equivalent to this matrix being skew-symmetric, nonsingular, and hollow (all diagonal entries are zero). This should not be confused with a symplectic matrix, which represents a symplectic transformation of the space. If ''V'' is finite-dimensional, then its dimension must necessarily be even since ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
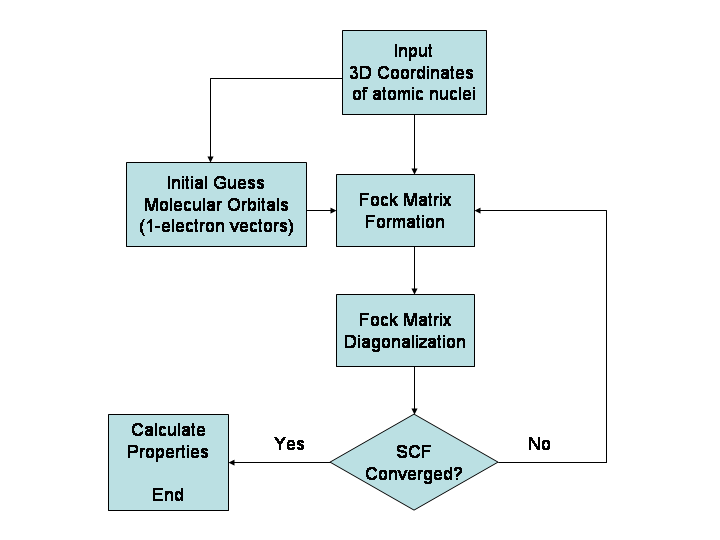
Hartree–Fock Method
In computational physics and chemistry, the Hartree–Fock (HF) method is a method of approximation for the determination of the wave function and the energy of a quantum many-body system in a stationary state. The Hartree–Fock method often assumes that the exact ''N''-body wave function of the system can be approximated by a single Slater determinant (in the case where the particles are fermions) or by a single permanent (in the case of bosons) of ''N'' spin-orbitals. By invoking the variational method, one can derive a set of ''N''-coupled equations for the ''N'' spin orbitals. A solution of these equations yields the Hartree–Fock wave function and energy of the system. Especially in the older literature, the Hartree–Fock method is also called the self-consistent field method (SCF). In deriving what is now called the Hartree equation as an approximate solution of the Schrödinger equation, Hartree required the final field as computed from the charge distribution to be "s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Superconductivity
Superconductivity is a set of physical properties observed in certain materials where electrical resistance vanishes and magnetic flux fields are expelled from the material. Any material exhibiting these properties is a superconductor. Unlike an ordinary metallic conductor, whose resistance decreases gradually as its temperature is lowered even down to near absolute zero, a superconductor has a characteristic critical temperature below which the resistance drops abruptly to zero. An electric current through a loop of superconducting wire can persist indefinitely with no power source. The superconductivity phenomenon was discovered in 1911 by Dutch physicist Heike Kamerlingh Onnes. Like ferromagnetism and atomic spectral lines, superconductivity is a phenomenon which can only be explained by quantum mechanics. It is characterized by the Meissner effect, the complete ejection of magnetic field lines from the interior of the superconductor during its transitions into the sup ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chirality
Chirality is a property of asymmetry important in several branches of science. The word ''chirality'' is derived from the Greek (''kheir''), "hand", a familiar chiral object. An object or a system is ''chiral'' if it is distinguishable from its mirror image; that is, it cannot be superimposed onto it. Conversely, a mirror image of an ''achiral'' object, such as a sphere, cannot be distinguished from the object. A chiral object and its mirror image are called ''enantiomorphs'' (Greek, "opposite forms") or, when referring to molecules, '' enantiomers''. A non-chiral object is called ''achiral'' (sometimes also ''amphichiral'') and can be superposed on its mirror image. The term was first used by Lord Kelvin in 1893 in the second Robert Boyle Lecture at the Oxford University Junior Scientific Club which was published in 1894: Human hands are perhaps the most recognized example of chirality. The left hand is a non-superimposable mirror image of the right hand; no matter ho ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Majorana Fermion
A Majorana fermion (, uploaded 19 April 2013, retrieved 5 October 2014; and also based on the pronunciation of physicist's name.), also referred to as a Majorana particle, is a fermion that is its own antiparticle. They were hypothesised by Ettore Majorana in 1937. The term is sometimes used in opposition to a Dirac fermion, which describes fermions that are not their own antiparticles. With the exception of neutrinos, all of the Standard Model fermions are known to behave as Dirac fermions at low energy (lower than the electroweak symmetry breaking temperature), and none are Majorana fermions. The nature of the neutrinos is not settled – they may turn out to be either Dirac or Majorana fermions. In condensed matter physics, quasiparticle excitations can appear like bound Majorana fermions. However, instead of a single fundamental particle, they are the collective movement of several individual particles (themselves composite) which are governed by non-Abelian statistics. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dirac Fermion
In physics, a Dirac fermion is a spin-½ particle (a fermion) which is different from its antiparticle. The vast majority of fermions – perhaps all – fall under this category. Description In particle physics, all fermions in the standard model have distinct antiparticles (''perhaps'' excepting neutrinos) and hence are Dirac fermions. They are named after Paul Dirac, and can be modeled with the Dirac equation. A Dirac fermion is equivalent to two Weyl fermions. The counterpart to a Dirac fermion is a Majorana fermion, a particle that must be its own antiparticle. Dirac quasi-particles In condensed matter physics, low-energy excitations in graphene and topological insulators, among others, are fermionic quasiparticles described by a pseudo-relativistic Dirac equation. See also * Dirac spinor, a wavefunction-like description of a Dirac fermion * Dirac–Kähler fermion, a geometric formulation of Dirac fermions * Majorana fermion, an alternate category of fermion, possibly de ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Charles Kittel
Charles Kittel (July 18, 1916 – May 15, 2019) was an American physicist. He was a professor at University of California, Berkeley from 1951 and was professor emeritus from 1978 until his death. Life and work Charles Kittel was born in New York City in 1916. He studied at the University of Cambridge, England, where he obtained his Bachelor of Arts (BA) in 1938. He published his thesis, under Gregory Breit, in 1941 at the University of Wisconsin–Madison and joined the Massachusetts Institute of Technology (MIT) between 1945 and 1947. During World War II, he joined the Submarine Operations Research Group (SORG). (He is mentioned on page 478 of RV Jones' book Most Secret War, published 1978.) He served in the United States Navy as a naval attache. From 1947 to 1951, he worked for Bell Laboratories, New Jersey, USA, especially on ferromagnetism. From 1951 to 1978, he worked at the University of California, Berkeley, where he taught and did research in the field of theoretical s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Antiferromagnetism
In materials that exhibit antiferromagnetism, the magnetic moments of atoms or molecules, usually related to the spins of electrons, align in a regular pattern with neighboring spins (on different sublattices) pointing in opposite directions. This is, like ferromagnetism and ferrimagnetism, a manifestation of ordered magnetism. The phenomenon of antiferromagnetism was first introduced by Lev Landau in 1933. Generally, antiferromagnetic order may exist at sufficiently low temperatures, but vanishes at and above the Néel temperature – named after Louis Néel, who had first identified this type of magnetic ordering. Above the Néel temperature, the material is typically paramagnetic. Measurement When no external field is applied, the antiferromagnetic structure corresponds to a vanishing total magnetization. In an external magnetic field, a kind of ferrimagnetic behavior may be displayed in the antiferromagnetic phase, with the absolute value of one of the sublattice magneti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Superfluidity
Superfluidity is the characteristic property of a fluid with zero viscosity which therefore flows without any loss of kinetic energy. When stirred, a superfluid forms vortices that continue to rotate indefinitely. Superfluidity occurs in two isotopes of helium (helium-3 and helium-4) when they are liquefied by cooling to cryogenic temperatures. It is also a property of various other exotic State of matter, states of matter theorized to exist in astrophysics, high-energy physics, and theories of quantum gravity. The theory of superfluidity was developed by Soviet theoretical physicists Lev Landau and Isaak Khalatnikov. Superfluidity is often coincidental with Bose–Einstein condensate, Bose–Einstein condensation, but neither phenomenon is directly related to the other; not all Bose–Einstein condensates can be regarded as superfluids, and not all superfluids are Bose–Einstein condensates. Superfluidity of liquid helium Superfluidity was discovered in helium-4 by Pyotr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nikolai Bogoliubov
Nikolay Nikolayevich Bogolyubov (russian: Никола́й Никола́евич Боголю́бов; 21 August 1909 – 13 February 1992), also transliterated as Bogoliubov and Bogolubov, was a Soviet and Russian mathematician and theoretical physicist known for a significant contribution to quantum field theory, classical and quantum statistical mechanics, and the theory of dynamical systems; he was the recipient of the 1992 Dirac Medal. Biography Early life (1909–1921) Nikolay Bogolyubov was born on 21 August 1909 in Nizhny Novgorod, Russian Empire to Russian Orthodox Church priest and seminary teacher of theology, psychology and philosophy Nikolay Mikhaylovich Bogolyubov, and Olga Nikolayevna Bogolyubova, a teacher of music. The Bogolyubovs relocated to the village of Velikaya Krucha in the Poltava Governorate (now in Poltava Oblast, Ukraine) in 1919, where the young Nikolay Bogolyubov began to study physics and mathematics. The family soon moved to Kiev in 1921, where ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |