|
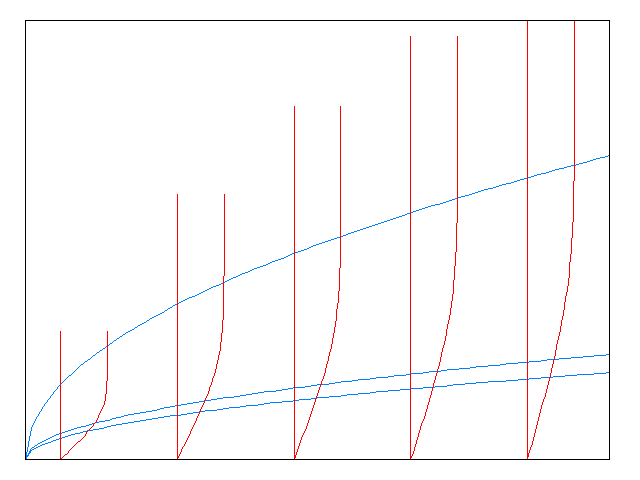
Blasius Equation
In physics and fluid mechanics, a Blasius boundary layer (named after Paul Richard Heinrich Blasius) describes the steady two-dimensional laminar boundary layer that forms on a semi-infinite plate which is held parallel to a constant unidirectional flow. Falkner and Skan later generalized Blasius' solution to wedge flow (Falkner–Skan boundary layer), i.e. flows in which the plate is not parallel to the flow. Prandtl's boundary layer equations Using scaling arguments, Ludwig Prandtl argued that about half of the terms in the Navier-Stokes equations are negligible in boundary layer flows (except in a small region near the leading edge of the plate). This leads to a reduced set of equations known as the boundary layer equations. For steady incompressible flow with constant viscosity and density, these read: Mass Continuity: \dfrac+\dfrac=0 x-Momentum: u \dfrac + v \dfrac = - \dfrac \dfrac + \dfrac y-Momentum: 0= - \dfrac \dfrac Here the coordinate system is chosen wi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Physics
Physics is the natural science that studies matter, its fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which relates to the order of nature, or, in other words, to the regular succession of events." Physics is one of the most fundamental scientific disciplines, with its main goal being to understand how the universe behaves. "Physics is one of the most fundamental of the sciences. Scientists of all disciplines use the ideas of physics, including chemists who study the structure of molecules, paleontologists who try to reconstruct how dinosaurs walked, and climatologists who study how human activities affect the atmosphere and oceans. Physics is also the foundation of all engineering and technology. No engineer could design a flat-screen TV, an interplanetary spacecraft, or even a better mousetrap without first understanding the basic laws of physics ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shooting Method
In numerical analysis, the shooting method is a method for solving a boundary value problem by reducing it to an initial value problem. It involves finding solutions to the initial value problem for different initial conditions until one finds the solution that also satisfies the boundary conditions of the boundary value problem. In layman's terms, one "shoots" out trajectories in different directions from one boundary until one finds the trajectory that "hits" the other boundary condition. Mathematical description Suppose one wants to solve the boundary-value problem y''(t) = f(t, y(t), y'(t)), \quad y(t_0) = y_0, \quad y(t_1) = y_1. Let y(t; a) solve the initial-value problem y''(t) = f(t, y(t), y'(t)), \quad y(t_0) = y_0, \quad y'(t_0) = a. If y(t_1; a) = y_1 , then y(t; a) is also a solution of the boundary-value problem. The shooting method is the process of solving the initial value problem for many different values of a until one finds the solution y(t; a) that sa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Specific Heat Ratio
In thermal physics and thermodynamics, the heat capacity ratio, also known as the adiabatic index, the ratio of specific heats, or Laplace's coefficient, is the ratio of the heat capacity at constant pressure () to heat capacity at constant volume (). It is sometimes also known as the ''isentropic expansion factor'' and is denoted by ( gamma) for an ideal gasγ first appeared in an article by the French mathematician, engineer, and physicist Siméon Denis Poisson: * On p. 332, Poisson defines γ merely as a small deviation from equilibrium which causes small variations of the equilibrium value of the density ρ. In Poisson's article of 1823 – * γ was expressed as a function of density D (p. 8) or of pressure P (p. 9). Meanwhile, in 1816 the French mathematician and physicist Pierre-Simon Laplace had found that the speed of sound depends on the ratio of the specific heats. * However, he didn't denote the ratio as γ. In 1825, Laplace stated that the speed of sound is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Howarth–Dorodnitsyn Transformation
In fluid dynamics, Howarth–Dorodnitsyn transformation (or Dorodnitsyn-Howarth transformation) is a density-weighted coordinate transformation, which reduces compressible flow conservation equations to simpler form (in most cases, to incompressible form). The transformation was first used by Anatoly Dorodnitsyn in 1942 and later by Leslie Howarth in 1948. The transformation of y coordinate (usually taken as the coordinate normal to the predominant flow direction) to \eta is given by :\eta = \int_0^y \frac \ dy, where \rho is the density and \rho_\infty is the density at infinity. The transformation is extensively used in boundary layer theory and other gas dynamics problems. Stewartson–Illingworth transformation Keith Stewartson and C. R. Illingworth, independently introduced in 1949, a transformation that extends the Howarth–Dorodnitsyn transformation. The transformation reads asN. Curle and HJ Davies: Modern Fluid Dynamics, Vol. 2, Compressible Flow :\xi = \int_0^x \frac\f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prandtl Number
The Prandtl number (Pr) or Prandtl group is a dimensionless number, named after the German physicist Ludwig Prandtl, defined as the ratio of momentum diffusivity to thermal diffusivity. The Prandtl number is given as: : \mathrm = \frac = \frac = \frac = \frac where: * \nu : momentum diffusivity (kinematic viscosity), \nu = \mu/\rho, ( SI units: m2/s) * \alpha : thermal diffusivity, \alpha = k/(\rho c_p), (SI units: m2/s) * \mu : dynamic viscosity, (SI units: Pa s = N s/m2) * k : thermal conductivity, (SI units: W/(m·K)) * c_p : specific heat, (SI units: J/(kg·K)) * \rho : density, (SI units: kg/m3). Note that whereas the Reynolds number and Grashof number are subscripted with a scale variable, the Prandtl number contains no such length scale and is dependent only on the fluid and the fluid state. The Prandtl number is often found in property tables alongside other properties such as viscosity and thermal conductivity. The mass transfer analog of the Prandtl number is the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Specific Enthalpy
Enthalpy , a property of a thermodynamic system, is the sum of the system's internal energy and the product of its pressure and volume. It is a state function used in many measurements in chemical, biological, and physical systems at a constant pressure, which is conveniently provided by the large ambient atmosphere. The pressure–volume term expresses the work required to establish the system's physical dimensions, i.e. to make room for it by displacing its surroundings. The pressure-volume term is very small for solids and liquids at common conditions, and fairly small for gases. Therefore, enthalpy is a stand-in for energy in chemical systems; bond, lattice, solvation and other "energies" in chemistry are actually enthalpy differences. As a state function, enthalpy depends only on the final configuration of internal energy, pressure, and volume, not on the path taken to achieve it. In the International System of Units (SI), the unit of measurement for enthalpy is the joule ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alan Arnold Griffith
Alan Arnold Griffith (13 June 1893 – 13 October 1963), son of Victorian science fiction writer George Griffith, was an English engineer. Among many other contributions he is best known for his work on stress and fracture in metals that is now known as metal fatigue, as well as being one of the first to develop a strong theoretical basis for the jet engine. Griffith's advanced axial-flow turbojet engine designs, were integral in the creation of Britain's first operational axial-flow turbojet engine, the Metropolitan-Vickers F.2 which first ran successfully in 1941. Griffith however had little direct involvement in actually producing the engine, after he moved in 1939 from leading the engine department at the Royal Aircraft Establishment to start work at Rolls-Royce. Early work A. A. Griffith took a first in mechanical engineering, followed by a master's degree and a Doctorate from the University of Liverpool. In 1915 he was accepted by the Royal Aircraft Factory as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parabolic Partial Differential Equation
A parabolic partial differential equation is a type of partial differential equation (PDE). Parabolic PDEs are used to describe a wide variety of time-dependent phenomena, including heat conduction, particle diffusion, and pricing of derivative investment instruments. Definition To define the simplest kind of parabolic PDE, consider a real-valued function u(x, y) of two independent real variables, x and y. A second-order, linear, constant-coefficient PDE for u takes the form :Au_ + 2Bu_ + Cu_ + Du_x + Eu_y + F = 0, and this PDE is classified as being ''parabolic'' if the coefficients satisfy the condition :B^2 - AC = 0. Usually x represents one-dimensional position and y represents time, and the PDE is solved subject to prescribed initial and boundary conditions. The name "parabolic" is used because the assumption on the coefficients is the same as the condition for the analytic geometry equation A x^2 + 2B xy + C y^2 + D x + E y + F = 0 to define a planar parabola. T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Richard Von Mises
Richard Edler von Mises (; 19 April 1883 – 14 July 1953) was an Austrian scientist and mathematician who worked on solid mechanics, fluid mechanics, aerodynamics, aeronautics, statistics and probability theory. He held the position of Gordon McKay Professor of Aerodynamics and Applied Mathematics at Harvard University. He described his work in his own words shortly before his death as being on :"... practical analysis, integral and differential equations, mechanics, hydrodynamics and aerodynamics, constructive geometry, probability calculus, statistics and philosophy." Although best known for his mathematical work, von Mises also contributed to the philosophy of science as a neo-positivist and empiricist, following the line of Ernst Mach. Historians of the Vienna Circle of logical empiricism recognize a "first phase" from 1907 through 1914 with Philipp Frank, Hans Hahn, and Otto Neurath. His older brother, Ludwig von Mises, held an opposite point of view with respect ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bryan Thwaites
Sir Bryan Thwaites, FIMA, FRSA (born 6 December 1923) is an English applied mathematician, educationalist and administrator. Early life Bryan Thwaites was born on 6 December 1923, the eldest son of Ernest and Dorothy Thwaites. He was educated at Dulwich College, from 1936–1940, and, thereafter, at Winchester College, aided in both colleges by scholarships. He was graduated with an MA from Clare College, Cambridge University, in 1944, gaining a First in the Maths Tripos. He received his doctorate (Ph.D.) from London University. Career Early career Thwaites' first appointment, on graduation, was as a Science Officer at the National Physical Laboratory (NPL), Teddington (1944–1947). He then moved to the Department of Aeronautics at the Imperial College of Science (1947–1951), where he made an early impression: his Thwaites Flap being used to assist aeronautical tests. At this time Thwaites also became an AFRAeS. Schoolmaster In 1951 he returned to his old school, Winche ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reynolds Number
In fluid mechanics, the Reynolds number () is a dimensionless quantity that helps predict fluid flow patterns in different situations by measuring the ratio between inertial and viscous forces. At low Reynolds numbers, flows tend to be dominated by laminar (sheet-like) flow, while at high Reynolds numbers flows tend to be turbulent. The turbulence results from differences in the fluid's speed and direction, which may sometimes intersect or even move counter to the overall direction of the flow (eddy currents). These eddy currents begin to churn the flow, using up energy in the process, which for liquids increases the chances of cavitation. The Reynolds number has wide applications, ranging from liquid flow in a pipe to the passage of air over an aircraft wing. It is used to predict the transition from laminar to turbulent flow and is used in the scaling of similar but different-sized flow situations, such as between an aircraft model in a wind tunnel and the full-size ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |