|
Bidirected Graph
In the mathematical domain of graph theory, a bidirected graph (introduced by ). Reprinted in ''Combinatorial Optimization — Eureka, You Shrink!'', Springer-Verlag, Lecture Notes in Computer Science 2570, 2003, pp. 27–30, . is a graph in which each edge is given an independent orientation (or direction, or arrow) at each end. Thus, there are three kinds of bidirected edges: those where the arrows point outward, towards the vertices, at both ends; those where both arrows point inward, away from the vertices; and those in which one arrow points away from its vertex and towards the opposite end, while the other arrow points in the same direction as the first, away from the opposite end and towards its own vertex. Edges of these three types may be called, respectively, extraverted, introverted, and directed. The "directed" edges are the same as ordinary directed edges in a directed graph; thus, a directed graph is a special kind of bidirected graph. It is sometimes desirable to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graph Theory
In mathematics, graph theory is the study of ''graphs'', which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of '' vertices'' (also called ''nodes'' or ''points'') which are connected by '' edges'' (also called ''links'' or ''lines''). A distinction is made between undirected graphs, where edges link two vertices symmetrically, and directed graphs, where edges link two vertices asymmetrically. Graphs are one of the principal objects of study in discrete mathematics. Definitions Definitions in graph theory vary. The following are some of the more basic ways of defining graphs and related mathematical structures. Graph In one restricted but very common sense of the term, a graph is an ordered pair G=(V,E) comprising: * V, a set of vertices (also called nodes or points); * E \subseteq \, a set of edges (also called links or lines), which are unordered pairs of vertices (that is, an edge is associated with t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graph (discrete Mathematics)
In discrete mathematics, and more specifically in graph theory, a graph is a structure amounting to a Set (mathematics), set of objects in which some pairs of the objects are in some sense "related". The objects correspond to mathematical abstractions called ''Vertex (graph theory), vertices'' (also called ''nodes'' or ''points'') and each of the related pairs of vertices is called an ''edge'' (also called ''link'' or ''line''). Typically, a graph is depicted in diagrammatic form as a set of dots or circles for the vertices, joined by lines or curves for the edges. Graphs are one of the objects of study in discrete mathematics. The edges may be directed or undirected. For example, if the vertices represent people at a party, and there is an edge between two people if they shake hands, then this graph is undirected because any person ''A'' can shake hands with a person ''B'' only if ''B'' also shakes hands with ''A''. In contrast, if an edge from a person ''A'' to a person ''B'' m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Directed Graph
In mathematics, and more specifically in graph theory, a directed graph (or digraph) is a graph that is made up of a set of vertices connected by directed edges, often called arcs. Definition In formal terms, a directed graph is an ordered pair where * ''V'' is a set whose elements are called '' vertices'', ''nodes'', or ''points''; * ''A'' is a set of ordered pairs of vertices, called ''arcs'', ''directed edges'' (sometimes simply ''edges'' with the corresponding set named ''E'' instead of ''A''), ''arrows'', or ''directed lines''. It differs from an ordinary or undirected graph, in that the latter is defined in terms of unordered pairs of vertices, which are usually called ''edges'', ''links'' or ''lines''. The aforementioned definition does not allow a directed graph to have multiple arrows with the same source and target nodes, but some authors consider a broader definition that allows directed graphs to have such multiple arcs (namely, they allow the arc set to be a m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Skew-symmetric Graph
In graph theory, a branch of mathematics, a skew-symmetric graph is a directed graph that is isomorphic to its own transpose graph, the graph formed by reversing all of its edges, under an isomorphism that is an involution without any fixed points. Skew-symmetric graphs are identical to the double covering graphs of bidirected graphs. Skew-symmetric graphs were first introduced under the name of ''antisymmetrical digraphs'' by , later as the double covering graphs of polar graphs by , and still later as the double covering graphs of bidirected graphs by . They arise in modeling the search for alternating paths and alternating cycles in algorithms for finding matchings in graphs, in testing whether a still life pattern in Conway's Game of Life may be partitioned into simpler components, in graph drawing, and in the implication graphs used to efficiently solve the 2-satisfiability problem. Definition As defined, e.g., by , a skew-symmetric graph ''G'' is a directed graph, toget ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bipartite Double Cover
In graph theory, the bipartite double cover of an undirected graph is a bipartite, covering graph of , with twice as many vertices as . It can be constructed as the tensor product of graphs, . It is also called the Kronecker double cover, canonical double cover or simply the bipartite double of . It should not be confused with a cycle double cover of a graph, a family of cycles that includes each edge twice. Construction The bipartite double cover of has two vertices and for each vertex of . Two vertices and are connected by an edge in the double cover if and only if and are connected by an edge in . For instance, below is an illustration of a bipartite double cover of a non-bipartite graph . In the illustration, each vertex in the tensor product is shown using a color from the first term of the product () and a shape from the second term of the product (); therefore, the vertices in the double cover are shown as circles while the vertices are shown as squares. : T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
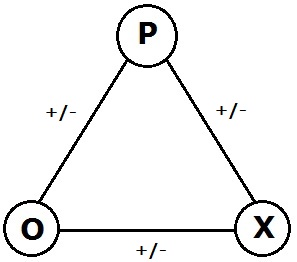
Signed Graph
In the area of graph theory in mathematics, a signed graph is a graph in which each edge has a positive or negative sign. A signed graph is balanced if the product of edge signs around every cycle is positive. The name "signed graph" and the notion of balance appeared first in a mathematical paper of Frank Harary in 1953. Dénes Kőnig had already studied equivalent notions in 1936 under a different terminology but without recognizing the relevance of the sign group. At the Center for Group Dynamics at the University of Michigan, Dorwin Cartwright and Harary generalized Fritz Heider's psychological theory of balance in triangles of sentiments to a psychological theory of balance in signed graphs. Signed graphs have been rediscovered many times because they come up naturally in many unrelated areas. For instance, they enable one to describe and analyze the geometry of subsets of the classical root systems. They appear in topological graph theory and group theory. They are a n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Undirected Graph
In discrete mathematics, and more specifically in graph theory, a graph is a structure amounting to a set of objects in which some pairs of the objects are in some sense "related". The objects correspond to mathematical abstractions called '' vertices'' (also called ''nodes'' or ''points'') and each of the related pairs of vertices is called an ''edge'' (also called ''link'' or ''line''). Typically, a graph is depicted in diagrammatic form as a set of dots or circles for the vertices, joined by lines or curves for the edges. Graphs are one of the objects of study in discrete mathematics. The edges may be directed or undirected. For example, if the vertices represent people at a party, and there is an edge between two people if they shake hands, then this graph is undirected because any person ''A'' can shake hands with a person ''B'' only if ''B'' also shakes hands with ''A''. In contrast, if an edge from a person ''A'' to a person ''B'' means that ''A'' owes money to ''B'', th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Skew-symmetric Graph
In graph theory, a branch of mathematics, a skew-symmetric graph is a directed graph that is isomorphic to its own transpose graph, the graph formed by reversing all of its edges, under an isomorphism that is an involution without any fixed points. Skew-symmetric graphs are identical to the double covering graphs of bidirected graphs. Skew-symmetric graphs were first introduced under the name of ''antisymmetrical digraphs'' by , later as the double covering graphs of polar graphs by , and still later as the double covering graphs of bidirected graphs by . They arise in modeling the search for alternating paths and alternating cycles in algorithms for finding matchings in graphs, in testing whether a still life pattern in Conway's Game of Life may be partitioned into simpler components, in graph drawing, and in the implication graphs used to efficiently solve the 2-satisfiability problem. Definition As defined, e.g., by , a skew-symmetric graph ''G'' is a directed graph, toget ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Signed Graph
In the area of graph theory in mathematics, a signed graph is a graph in which each edge has a positive or negative sign. A signed graph is balanced if the product of edge signs around every cycle is positive. The name "signed graph" and the notion of balance appeared first in a mathematical paper of Frank Harary in 1953. Dénes Kőnig had already studied equivalent notions in 1936 under a different terminology but without recognizing the relevance of the sign group. At the Center for Group Dynamics at the University of Michigan, Dorwin Cartwright and Harary generalized Fritz Heider's psychological theory of balance in triangles of sentiments to a psychological theory of balance in signed graphs. Signed graphs have been rediscovered many times because they come up naturally in many unrelated areas. For instance, they enable one to describe and analyze the geometry of subsets of the classical root systems. They appear in topological graph theory and group theory. They are a n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |