|
Barrier Option
A barrier option is an option whose payoff is conditional upon the underlying asset's price breaching a barrier level during the option's lifetime. Types Barrier options are path-dependent exotics that are similar in some ways to ordinary options. You can call or put in American, Bermudan, or European exercise style. But they become activated (or extinguished) only if the underlying breaches a predetermined level (the barrier). "In" options only become active in the event that a predetermined knock-in barrier price is breached: # If the barrier price is far from being breached, the knock-in option will be worth slightly more than zero. # If the barrier price is close to being breached, the knock-in option will be worth slightly less than the corresponding vanilla option. # If the barrier price has been breached, the knock-in option will trade at the exact same value as the corresponding vanilla option. "Out" options start their lives active and become null and void in the event ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exotic Derivatives
An exotic derivative, in finance, is a derivative which is more complex than commonly traded "vanilla" products. This complexity usually relates to determination of payoff; see option style. The category may also include derivatives with a non-standard subject matter - i.e., underlying - developed for a particular client or a particular market.Understanding derivative contracts: types of derivatives The term "exotic derivative" has no precisely defined meaning, being a colloquialism that reflects how common a particular derivative is in the marketplace. As such, certain derivative instruments have been considered exotic when conceived of and sold, but lost this status when they were traded with significant enough volume. Examples of this phenomenon include [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Volatility Smile
Volatility smiles are implied volatility patterns that arise in pricing financial options. It is a parameter (implied volatility) that is needed to be modified for the Black–Scholes formula to fit market prices. In particular for a given expiration, options whose strike price differs substantially from the underlying asset's price command higher prices (and thus implied volatilities) than what is suggested by standard option pricing models. These options are said to be either deep in-the-money or out-of-the-money. Graphing implied volatilities against strike prices for a given expiry produces a skewed "smile" instead of the expected flat surface. The pattern differs across various markets. Equity options traded in American markets did not show a volatility smile before the Crash of 1987 but began showing one afterwards. It is believed that investor reassessments of the probabilities of fat-tail have led to higher prices for out-of-the-money options. This anomaly implies de ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Finite Difference Method
In numerical analysis, finite-difference methods (FDM) are a class of numerical techniques for solving differential equations by approximating derivatives with finite differences. Both the spatial domain and time interval (if applicable) are discretized, or broken into a finite number of steps, and the value of the solution at these discrete points is approximated by solving algebraic equations containing finite differences and values from nearby points. Finite difference methods convert ordinary differential equations (ODE) or partial differential equations (PDE), which may be nonlinear, into a system of linear equations that can be solved by matrix algebra techniques. Modern computers can perform these linear algebra computations efficiently which, along with their relative ease of implementation, has led to the widespread use of FDM in modern numerical analysis. Today, FDM are one of the most common approaches to the numerical solution of PDE, along with finite element metho ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heat Equation
In mathematics and physics, the heat equation is a certain partial differential equation. Solutions of the heat equation are sometimes known as caloric functions. The theory of the heat equation was first developed by Joseph Fourier in 1822 for the purpose of modeling how a quantity such as heat diffuses through a given region. As the prototypical parabolic partial differential equation, the heat equation is among the most widely studied topics in pure mathematics, and its analysis is regarded as fundamental to the broader field of partial differential equations. The heat equation can also be considered on Riemannian manifolds, leading to many geometric applications. Following work of Subbaramiah Minakshisundaram and Åke Pleijel, the heat equation is closely related with spectral geometry. A seminal nonlinear variant of the heat equation was introduced to differential geometry by James Eells and Joseph Sampson in 1964, inspiring the introduction of the Ricci flow by Richard ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Finite Difference Methods For Option Pricing
Finite difference methods for option pricing are numerical methods used in mathematical finance for the valuation of options. Finite difference methods were first applied to option pricing by Eduardo Schwartz in 1977. In general, finite difference methods are used to price options by approximating the (continuous-time) differential equation that describes how an option price evolves over time by a set of (discrete-time) difference equations. The discrete difference equations may then be solved iteratively to calculate a price for the option. Phil Goddard (N.D.).''Option Pricing – Finite Difference Methods''/ref> The approach arises since the evolution of the option value can be modelled via a partial differential equation (PDE), as a function of (at least) time and price of underlying; see for example the Black–Scholes PDE. Once in this form, a finite difference model can be derived, and the valuation obtained. The approach can be used to solve derivative pricing problems ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
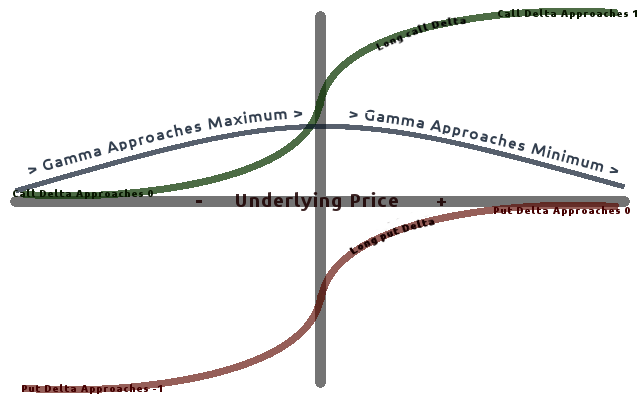
Greeks (finance)
In mathematical finance, the Greeks are the quantities representing the sensitivity of the price of derivatives such as options to a change in underlying parameters on which the value of an instrument or portfolio of financial instruments is dependent. The name is used because the most common of these sensitivities are denoted by Greek letters (as are some other finance measures). Collectively these have also been called the risk sensitivities, risk measures or hedge parameters. Use of the Greeks The Greeks are vital tools in risk management. Each Greek measures the sensitivity of the value of a portfolio to a small change in a given underlying parameter, so that component risks may be treated in isolation, and the portfolio rebalanced accordingly to achieve a desired exposure; see for example delta hedging. The Greeks in the Black–Scholes model are relatively easy to calculate, a desirable property of financial models, and are very useful for derivatives traders, especi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Monte Carlo Option Model
In mathematical finance, a Monte Carlo option model uses Monte Carlo methodsAlthough the term 'Monte Carlo method' was coined by Stanislaw Ulam in the 1940s, some trace such methods to the 18th century French naturalist Buffon, and a question he asked about the results of dropping a needle randomly on a striped floor or table. See Buffon's needle. to calculate the value of an option with multiple sources of uncertainty or with complicated features. The first application to option pricing was by Phelim Boyle in 1977 (for European options). In 1996, M. Broadie and P. Glasserman showed how to price Asian options by Monte Carlo. An important development was the introduction in 1996 by Carriere of Monte Carlo methods for options with early exercise features. Methodology In terms of theory, Monte Carlo valuation relies on risk neutral valuation.Marco DiasReal Options with Monte Carlo Simulation/ref> Here the price of the option is its discounted expected value; see risk neutrality an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boundary Condition
In mathematics, in the field of differential equations, a boundary value problem is a differential equation together with a set of additional constraints, called the boundary conditions. A solution to a boundary value problem is a solution to the differential equation which also satisfies the boundary conditions. Boundary value problems arise in several branches of physics as any physical differential equation will have them. Problems involving the wave equation, such as the determination of normal modes, are often stated as boundary value problems. A large class of important boundary value problems are the Sturm–Liouville problems. The analysis of these problems involves the eigenfunctions of a differential operator. To be useful in applications, a boundary value problem should be well posed. This means that given the input to the problem there exists a unique solution, which depends continuously on the input. Much theoretical work in the field of partial differential eq ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Differential Equation
In mathematics, a partial differential equation (PDE) is an equation which imposes relations between the various partial derivatives of a Multivariable calculus, multivariable function. The function is often thought of as an "unknown" to be solved for, similarly to how is thought of as an unknown number to be solved for in an algebraic equation like . However, it is usually impossible to write down explicit formulas for solutions of partial differential equations. There is, correspondingly, a vast amount of modern mathematical and scientific research on methods to Numerical methods for partial differential equations, numerically approximate solutions of certain partial differential equations using computers. Partial differential equations also occupy a large sector of pure mathematics, pure mathematical research, in which the usual questions are, broadly speaking, on the identification of general qualitative features of solutions of various partial differential equations, such a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Replicating Portfolio
In mathematical finance, a replicating portfolio for a given asset or series of cash flows is a portfolio of assets with the same properties (especially cash flows). This is meant in two distinct senses: static replication, where the portfolio has the same cash flows as the reference asset (and no changes need to be made to maintain this), and dynamic replication, where the portfolio does not have the same cash flows, but has the same "Greeks" as the reference asset, meaning that for small (properly, infinitesimal) changes to underlying market parameters, the price of the asset and the price of the portfolio change in the same way. Dynamic replication requires continual adjustment, as the asset and portfolio are only assumed to behave similarly at a single point (mathematically, their partial derivatives are equal at a single point). Given an asset or liability, an offsetting replicating portfolio (a "hedge") is called a static hedge or dynamic hedge, and constructing such a portfoli ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Option (finance)
In finance, an option is a contract which conveys to its owner, the ''holder'', the right, but not the obligation, to buy or sell a specific quantity of an underlying asset or instrument at a specified strike price on or before a specified date, depending on the style of the option. Options are typically acquired by purchase, as a form of compensation, or as part of a complex financial transaction. Thus, they are also a form of asset and have a valuation that may depend on a complex relationship between underlying asset price, time until expiration, market volatility, the risk-free rate of interest, and the strike price of the option. Options may be traded between private parties in ''over-the-counter'' (OTC) transactions, or they may be exchange-traded in live, public markets in the form of standardized contracts. Definition and application An option is a contract that allows the holder the right to buy or sell an underlying asset or financial instrument at a specified strike ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |