|
Brownian Model Of Financial Markets
The Brownian motion models for financial markets are based on the work of Robert C. Merton and Paul A. Samuelson, as extensions to the one-period market models of Harold Markowitz and William F. Sharpe, and are concerned with defining the concepts of financial assets and markets, portfolios, gains and wealth in terms of continuous-time stochastic processes. Under this model, these assets have continuous prices evolving continuously in time and are driven by Brownian motion processes. This model requires an assumption of perfectly divisible assets and a frictionless market (i.e. that no transaction costs occur either for buying or selling). Another assumption is that asset prices have no jumps, that is there are no surprises in the market. This last assumption is removed in jump diffusion models. Financial market processes Consider a financial market consisting of N + 1 financial assets, where one of these assets, called a ''bond'' or ''money market'', is risk free while the remain ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Brownian Motion
Brownian motion, or pedesis (from grc, πήδησις "leaping"), is the random motion of particles suspended in a medium (a liquid or a gas). This pattern of motion typically consists of random fluctuations in a particle's position inside a fluid sub-domain, followed by a relocation to another sub-domain. Each relocation is followed by more fluctuations within the new closed volume. This pattern describes a fluid at thermal equilibrium, defined by a given temperature. Within such a fluid, there exists no preferential direction of flow (as in transport phenomena). More specifically, the fluid's overall linear and angular momenta remain null over time. The kinetic energies of the molecular Brownian motions, together with those of molecular rotations and vibrations, sum up to the caloric component of a fluid's internal energy (the equipartition theorem). This motion is named after the botanist Robert Brown, who first described the phenomenon in 1827, while looking throu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Space
In probability theory, a probability space or a probability triple (\Omega, \mathcal, P) is a mathematical construct that provides a formal model of a random process or "experiment". For example, one can define a probability space which models the throwing of a die. A probability space consists of three elements:Stroock, D. W. (1999). Probability theory: an analytic view. Cambridge University Press. # A sample space, \Omega, which is the set of all possible outcomes. # An event space, which is a set of events \mathcal, an event being a set of outcomes in the sample space. # A probability function, which assigns each event in the event space a probability, which is a number between 0 and 1. In order to provide a sensible model of probability, these elements must satisfy a number of axioms, detailed in this article. In the example of the throw of a standard die, we would take the sample space to be \. For the event space, we could simply use the set of all subsets of the sample ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Almost Surely
In probability theory, an event is said to happen almost surely (sometimes abbreviated as a.s.) if it happens with probability 1 (or Lebesgue measure 1). In other words, the set of possible exceptions may be non-empty, but it has probability 0. The concept is analogous to the concept of "almost everywhere" in measure theory. In probability experiments on a finite sample space, there is no difference between ''almost surely'' and ''surely'' (since having a probability of 1 often entails including all the sample points). However, this distinction becomes important when the sample space is an infinite set, because an infinite set can have non-empty subsets of probability 0. Some examples of the use of this concept include the strong and uniform versions of the law of large numbers, and the continuity of the paths of Brownian motion. The terms almost certainly (a.c.) and almost always (a.a.) are also used. Almost never describes the opposite of ''almost surely'': an event that h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dividend
A dividend is a distribution of profits by a corporation to its shareholders. When a corporation earns a profit or surplus, it is able to pay a portion of the profit as a dividend to shareholders. Any amount not distributed is taken to be re-invested in the business (called retained earnings). The current year profit as well as the retained earnings of previous years are available for distribution; a corporation is usually prohibited from paying a dividend out of its capital. Distribution to shareholders may be in cash (usually a deposit into a bank account) or, if the corporation has a dividend reinvestment plan, the amount can be paid by the issue of further shares or by share repurchase. In some cases, the distribution may be of assets. The dividend received by a shareholder is income of the shareholder and may be subject to income tax (see dividend tax). The tax treatment of this income varies considerably between jurisdictions. The corporation does not receive a tax deduct ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arbitrage
In economics and finance, arbitrage (, ) is the practice of taking advantage of a difference in prices in two or more markets; striking a combination of matching deals to capitalise on the difference, the profit being the difference between the market prices at which the unit is traded. When used by academics, an arbitrage is a transaction that involves no negative cash flow at any probabilistic or temporal state and a positive cash flow in at least one state; in simple terms, it is the possibility of a risk-free profit after transaction costs. For example, an arbitrage opportunity is present when there is the possibility to instantaneously buy something for a low price and sell it for a higher price. In principle and in academic use, an arbitrage is risk-free; in common use, as in statistical arbitrage, it may refer to ''expected'' profit, though losses may occur, and in practice, there are always risks in arbitrage, some minor (such as fluctuation of prices decreasing profit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
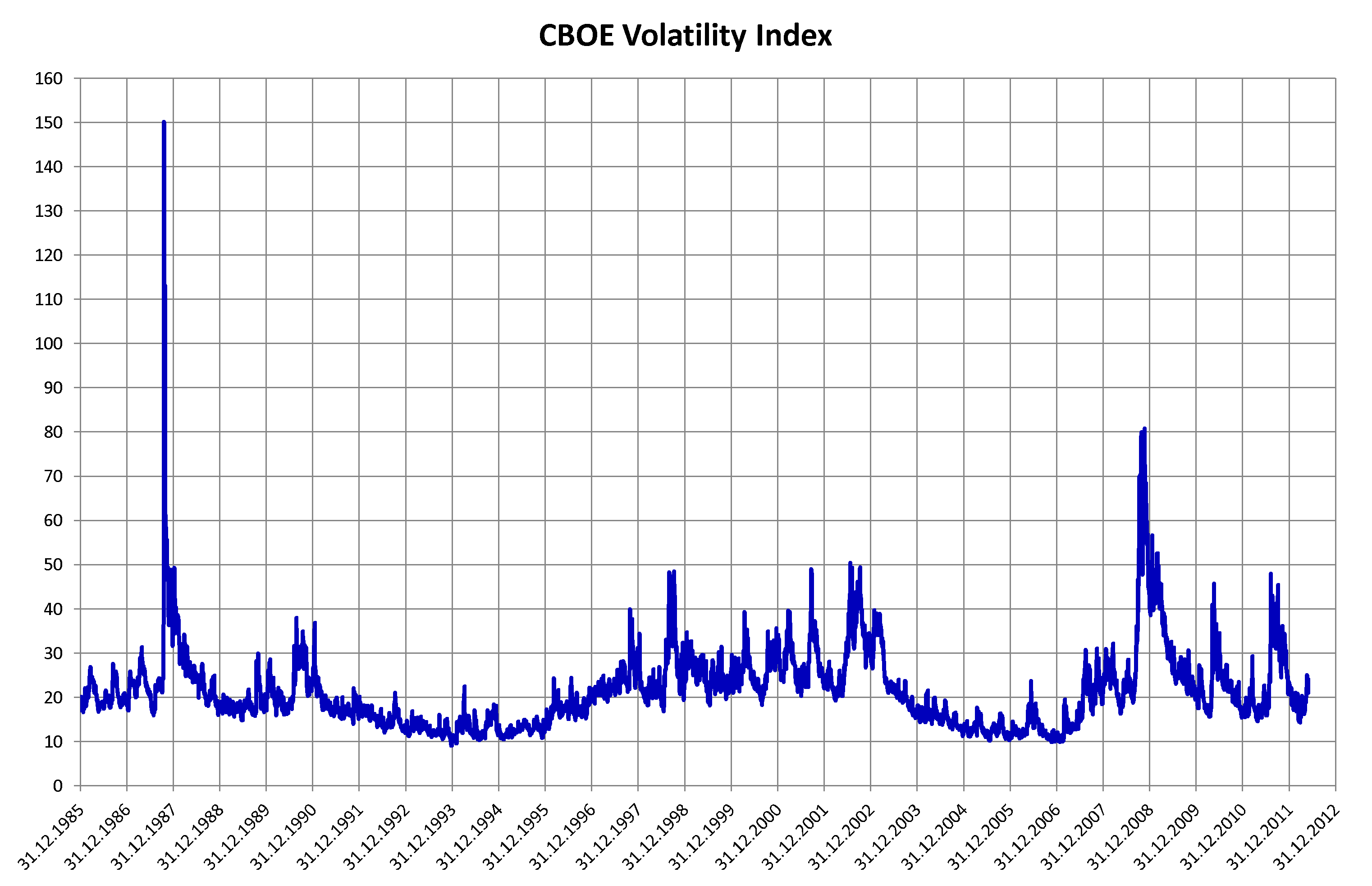
Volatility (finance)
In finance, volatility (usually denoted by ''σ'') is the degree of variation of a trading price series over time, usually measured by the standard deviation of logarithmic returns. Historic volatility measures a time series of past market prices. Implied volatility looks forward in time, being derived from the market price of a market-traded derivative (in particular, an option). Volatility terminology Volatility as described here refers to the actual volatility, more specifically: * actual current volatility of a financial instrument for a specified period (for example 30 days or 90 days), based on historical prices over the specified period with the last observation the most recent price. * actual historical volatility which refers to the volatility of a financial instrument over a specified period but with the last observation on a date in the past **near synonymous is realized volatility, the square root of the realized variance, in turn calculated using the sum of squ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stochastic Differential Equation
A stochastic differential equation (SDE) is a differential equation in which one or more of the terms is a stochastic process, resulting in a solution which is also a stochastic process. SDEs are used to model various phenomena such as stock prices or physical systems subject to thermal fluctuations. Typically, SDEs contain a variable which represents random white noise calculated as the derivative of Brownian motion or the Wiener process. However, other types of random behaviour are possible, such as jump processes. Random differential equations are conjugate to stochastic differential equations. Background Stochastic differential equations originated in the theory of Brownian motion, in the work of Albert Einstein and Smoluchowski. These early examples were linear stochastic differential equations, also called 'Langevin' equations after French physicist Langevin, describing the motion of a harmonic oscillator subject to a random force. The mathematical theory of stochasti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lebesgue's Decomposition Theorem
In mathematics, more precisely in measure theory, Lebesgue's decomposition theorem states that for every two σ-finite signed measures \mu and \nu on a measurable space (\Omega,\Sigma), there exist two σ-finite signed measures \nu_0 and \nu_1 such that: * \nu=\nu_0+\nu_1\, * \nu_0\ll\mu (that is, \nu_0 is absolutely continuous with respect to \mu) * \nu_1\perp\mu (that is, \nu_1 and \mu are singular). These two measures are uniquely determined by \mu and \nu. Refinement Lebesgue's decomposition theorem can be refined in a number of ways. First, the decomposition of the singular part of a regular Borel measure on the real line can be refined: :\, \nu = \nu_ + \nu_ + \nu_ where * ''ν''cont is the absolutely continuous part * ''ν''sing is the singular continuous part * ''ν''pp is the pure point part (a discrete measure). Second, absolutely continuous measures are classified by the Radon–Nikodym theorem, and discrete measures are easily understood. Hence (singular cont ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Absolute Continuity
In calculus, absolute continuity is a smoothness property of functions that is stronger than continuity and uniform continuity. The notion of absolute continuity allows one to obtain generalizations of the relationship between the two central operations of calculus— differentiation and integration. This relationship is commonly characterized (by the fundamental theorem of calculus) in the framework of Riemann integration, but with absolute continuity it may be formulated in terms of Lebesgue integration. For real-valued functions on the real line, two interrelated notions appear: absolute continuity of functions and absolute continuity of measures. These two notions are generalized in different directions. The usual derivative of a function is related to the '' Radon–Nikodym derivative'', or ''density'', of a measure. We have the following chains of inclusions for functions over a compact subset of the real line: : ''absolutely continuous'' ⊆ ''uniformly continuous'' = ''con ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bounded Variation
In mathematical analysis, a function of bounded variation, also known as ' function, is a real-valued function whose total variation is bounded (finite): the graph of a function having this property is well behaved in a precise sense. For a continuous function of a single variable, being of bounded variation means that the distance along the direction of the -axis, neglecting the contribution of motion along -axis, traveled by a point moving along the graph has a finite value. For a continuous function of several variables, the meaning of the definition is the same, except for the fact that the continuous path to be considered cannot be the whole graph of the given function (which is a hypersurface in this case), but can be every intersection of the graph itself with a hyperplane (in the case of functions of two variables, a plane) parallel to a fixed -axis and to the -axis. Functions of bounded variation are precisely those with respect to which one may find Riemann–Stieltj ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continuous Function
In mathematics, a continuous function is a function such that a continuous variation (that is a change without jump) of the argument induces a continuous variation of the value of the function. This means that there are no abrupt changes in value, known as '' discontinuities''. More precisely, a function is continuous if arbitrarily small changes in its value can be assured by restricting to sufficiently small changes of its argument. A discontinuous function is a function that is . Up until the 19th century, mathematicians largely relied on intuitive notions of continuity, and considered only continuous functions. The epsilon–delta definition of a limit was introduced to formalize the definition of continuity. Continuity is one of the core concepts of calculus and mathematical analysis, where arguments and values of functions are real and complex numbers. The concept has been generalized to functions between metric spaces and between topological spaces. The latter are the mo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Augmented Filtration
Augment or augmentation may refer to: Language *Augment (Indo-European), a syllable added to the beginning of the word in certain Indo-European languages *Augment (Bantu languages), a morpheme that is prefixed to the noun class prefix of nouns in certain Bantu languages *Augment, a name sometimes given to the verbal ''ō-'' prefix in Nahuatl grammar Technology *Augmentation (obstetrics), the process by which the first and/or second stages of an already established labour is accelerated or potentiated by deliberate and artificial means *Augmentation (pharmacology), the combination of two or more drugs to achieve better treatment results *Augmented reality, a live view of a physical, real-world environment whose elements are ''augmented'' by computer-generated sensory input *Augmented cognition, a research field that aims at creating revolutionary human-computer interactions *Augment (Tymshare), a hypertext system derived from Douglas Engelbart's oN-Line System, renamed "Augment" b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |