|
Boyer–Lindquist Coordinates
In the mathematical description of general relativity, the Boyer–Lindquist coordinates are a generalization of the coordinates used for the metric of a Schwarzschild black hole that can be used to express the metric of a Kerr black hole. The Hamiltonian for test particle motion in Kerr spacetime is separable in Boyer–Lindquist coordinates. Using Hamilton–Jacobi theory one can derive a fourth constant of the motion known as Carter's constant. The 1967 paper introducing Boyer–Lindquist coordinates was a posthumous publication for Robert H. Boyer, who was killed in the 1966 University of Texas tower shooting. Line element The line element for a black hole with a total mass equivalent M, angular momentum J, and charge Q in Boyer–Lindquist coordinates and natural units (G=c=1) is : ds^2 = -\frac\left(dt - a \sin^2\theta \,d\phi \right)^2 +\frac\Big(\left(r^2+a^2\right)\,d\phi - a \,dt\Big)^2 + \fracdr^2 + \rho^2 \,d\theta^2 where :\Delta = r^2 - 2Mr + a^2 + Q^2, called th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
General Relativity
General relativity, also known as the general theory of relativity and Einstein's theory of gravity, is the geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of gravitation in modern physics. General relativity generalizes special relativity and refines Newton's law of universal gravitation, providing a unified description of gravity as a geometric property of space and time or four-dimensional spacetime. In particular, the ' is directly related to the energy and momentum of whatever matter and radiation are present. The relation is specified by the Einstein field equations, a system of second order partial differential equations. Newton's law of universal gravitation, which describes classical gravity, can be seen as a prediction of general relativity for the almost flat spacetime geometry around stationary mass distributions. Some predictions of general relativity, however, are beyond Newton's law of universal gr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
One-form
In differential geometry, a one-form on a differentiable manifold is a smooth section of the cotangent bundle. Equivalently, a one-form on a manifold M is a smooth mapping of the total space of the tangent bundle of M to \R whose restriction to each fibre is a linear functional on the tangent space. Symbolically, \alpha : TM \rightarrow ,\quad \alpha_x = \alpha, _: T_xM \rightarrow , where \alpha_x is linear. Often one-forms are described locally, particularly in local coordinates. In a local coordinate system, a one-form is a linear combination of the differentials of the coordinates: \alpha_x = f_1(x) \, dx_1 + f_2(x) \, dx_2 + \cdots + f_n(x) \, dx_n , where the f_i are smooth functions. From this perspective, a one-form has a covariant transformation law on passing from one coordinate system to another. Thus a one-form is an order 1 covariant tensor field. Examples The most basic non-trivial differential one-form is the "change in angle" form d\theta. This is defined ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Energy–momentum Tensor
{{dab ...
Energy–momentum may refer to: * Four-momentum *Stress–energy tensor *Energy–momentum relation In physics, the energy–momentum relation, or relativistic dispersion relation, is the relativistic equation relating total energy (which is also called relativistic energy) to invariant mass (which is also called rest mass) and momentum. It is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electromagnetic Stress Tensor
The Maxwell stress tensor (named after James Clerk Maxwell) is a symmetric second-order tensor used in classical electromagnetism to represent the interaction between electromagnetic forces and mechanical momentum. In simple situations, such as a point charge moving freely in a homogeneous magnetic field, it is easy to calculate the forces on the charge from the Lorentz force law. When the situation becomes more complicated, this ordinary procedure can become impractically difficult, with equations spanning multiple lines. It is therefore convenient to collect many of these terms in the Maxwell stress tensor, and to use tensor arithmetic to find the answer to the problem at hand. In the relativistic formulation of electromagnetism, the Maxwell's tensor appears as a part of the electromagnetic stress–energy tensor which is the electromagnetic component of the total stress–energy tensor. The latter describes the density and flux of energy and momentum in spacetime. Motivation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ricci Tensor
In differential geometry, the Ricci curvature tensor, named after Gregorio Ricci-Curbastro, is a geometric object which is determined by a choice of Riemannian or pseudo-Riemannian metric on a manifold. It can be considered, broadly, as a measure of the degree to which the geometry of a given metric tensor differs locally from that of ordinary Euclidean space or pseudo-Euclidean space. The Ricci tensor can be characterized by measurement of how a shape is deformed as one moves along geodesics in the space. In general relativity, which involves the pseudo-Riemannian setting, this is reflected by the presence of the Ricci tensor in the Raychaudhuri equation. Partly for this reason, the Einstein field equations propose that spacetime can be described by a pseudo-Riemannian metric, with a strikingly simple relationship between the Ricci tensor and the matter content of the universe. Like the metric tensor, the Ricci tensor assigns to each tangent space of the manifold a symmetri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Twistor Theory
In theoretical physics, twistor theory was proposed by Roger Penrose in 1967 as a possible path to quantum gravity and has evolved into a branch of theoretical and mathematical physics. Penrose proposed that twistor space should be the basic arena for physics from which space-time itself should emerge. It leads to a powerful set of mathematical tools that have applications to differential and integral geometry, nonlinear differential equations and representation theory and in physics to general relativity and quantum field theory, in particular to scattering amplitudes. Development seems to be indirectly influenced by Einstein–Cartan–Sciama–Kibble theory. Overview Mathematically, projective twistor space \mathbb is a 3-dimensional complex manifold, complex projective 3-space \mathbb^3. It has the physical interpretation of the space of massless particles with spin. It is the projectivisation of a 4-dimensional complex vector space, non-projective twistor space \mathb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spinor
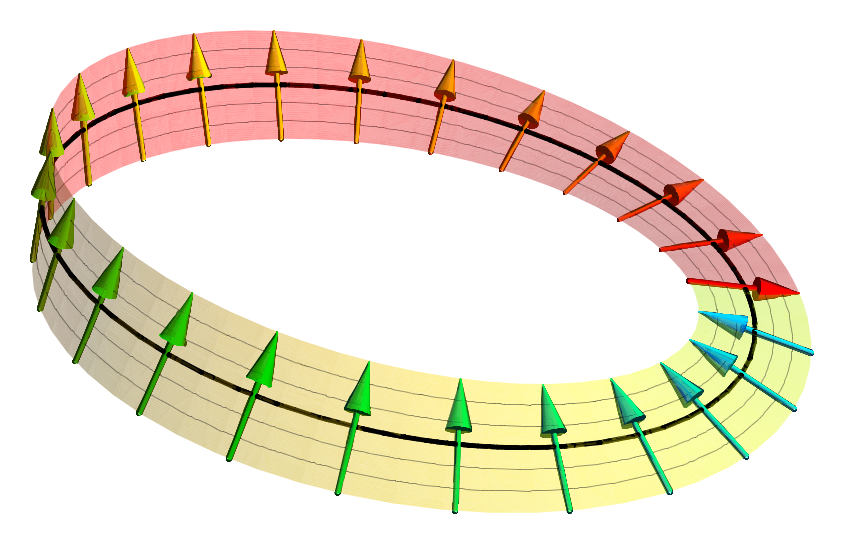
In geometry and physics, spinors are elements of a complex vector space that can be associated with Euclidean space. Like geometric vectors and more general tensors, spinors transform linearly when the Euclidean space is subjected to a slight ( infinitesimal) rotation. Unlike vectors and tensors, a spinor transforms to its negative when the space is continuously rotated through a complete turn from 0° to 360° (see picture). This property characterizes spinors: spinors can be viewed as the "square roots" of vectors (although this is inaccurate and may be misleading; they are better viewed as "square roots" of sections of vector bundles – in the case of the exterior algebra bundle of the cotangent bundle, they thus become "square roots" of differential forms). It is also possible to associate a substantially similar notion of spinor to Minkowski space, in which case the Lorentz transformations of special relativity play the role of rotations. Spinors were introduced in ge ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Riemann Curvature Tensor
In the mathematical field of differential geometry, the Riemann curvature tensor or Riemann–Christoffel tensor (after Bernhard Riemann and Elwin Bruno Christoffel) is the most common way used to express the curvature of Riemannian manifolds. It assigns a tensor to each point of a Riemannian manifold (i.e., it is a tensor field). It is a local invariant of Riemannian metrics which measures the failure of the second covariant derivatives to commute. A Riemannian manifold has zero curvature if and only if it is ''flat'', i.e. locally isometric to the Euclidean space. The curvature tensor can also be defined for any pseudo-Riemannian manifold, or indeed any manifold equipped with an affine connection. It is a central mathematical tool in the theory of general relativity, the modern theory of gravity, and the curvature of spacetime is in principle observable via the geodesic deviation equation. The curvature tensor represents the tidal force experienced by a rigid body movin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Contorsion Tensor
The contorsion tensor in differential geometry is the difference between a connection with and without torsion in it. It commonly appears in the study of spin connections. Thus, for example, a vielbein together with a spin connection, when subject to the condition of vanishing torsion, gives a description of Einstein gravity. For supersymmetry, the same constraint, of vanishing torsion, gives (the field equations of) 11-dimensional supergravity. That is, the contorsion tensor, along with the connection, becomes one of the dynamical objects of the theory, demoting the metric to a secondary, derived role. The elimination of torsion in a connection is referred to as the ''absorption of torsion'', and is one of the steps of Cartan's equivalence method for establishing the equivalence of geometric structures. Definition in metric geometry In metric geometry, the contorsion tensor expresses the difference between a metric-compatible affine connection with Christoffel symbol \G ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spin Connection
In differential geometry and mathematical physics, a spin connection is a connection on a spinor bundle. It is induced, in a canonical manner, from the affine connection. It can also be regarded as the gauge field generated by local Lorentz transformations. In some canonical formulations of general relativity, a spin connection is defined on spatial slices and can also be regarded as the gauge field generated by local rotations. The spin connection occurs in two common forms: the ''Levi-Civita spin connection'', when it is derived from the Levi-Civita connection, and the ''affine spin connection'', when it is obtained from the affine connection. The difference between the two of these is that the Levi-Civita connection is by definition the unique torsion-free connection, whereas the affine connection (and so the affine spin connection) may contain torsion. Definition Let e_\mu^ be the local Lorentz frame fields or vierbein (also known as a tetrad), which is a set of ortho ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Torsion Tensor
In differential geometry, the notion of torsion is a manner of characterizing a twist or screw of a moving frame around a curve. The torsion of a curve, as it appears in the Frenet–Serret formulas, for instance, quantifies the twist of a curve about its tangent vector as the curve evolves (or rather the rotation of the Frenet–Serret frame about the tangent vector). In the geometry of surfaces, the ''geodesic torsion'' describes how a surface twists about a curve on the surface. The companion notion of curvature measures how moving frames "roll" along a curve "without twisting". More generally, on a differentiable manifold equipped with an affine connection (that is, a connection in the tangent bundle), torsion and curvature form the two fundamental invariants of the connection. In this context, torsion gives an intrinsic characterization of how tangent spaces twist about a curve when they are parallel transported; whereas curvature describes how the tangent spaces r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Minkowski Metric
In mathematical physics, Minkowski space (or Minkowski spacetime) () is a combination of three-dimensional Euclidean space and time into a four-dimensional manifold where the spacetime interval between any two events is independent of the inertial frame of reference in which they are recorded. Although initially developed by mathematician Hermann Minkowski for Maxwell's equations of electromagnetism, the mathematical structure of Minkowski spacetime was shown to be implied by the postulates of special relativity. Minkowski space is closely associated with Einstein's theories of special relativity and general relativity and is the most common mathematical structure on which special relativity is formulated. While the individual components in Euclidean space and time may differ due to length contraction and time dilation, in Minkowski spacetime, all frames of reference will agree on the total distance in spacetime between events.This makes spacetime distance an invariant. Because ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |