|
Boschloo's Test
Boschloo's test is a statistical hypothesis test for analysing 2x2 contingency tables. It examines the association of two Bernoulli distributed random variables and is a uniformly more powerful alternative to Fisher's exact test. It was proposed in 1970 by R. D. Boschloo. Setting A 2x2 contingency table visualizes n independent observations of two binary variables A and B: : \begin & B = 1 & B = 0 & \mbox\\ \hline A = 1 & x_ & x_ & n_1 \\ A = 0 & x_ & x_ & n_0 \\ \hline \mbox & s_1 & s_0 & n\\ \end The probability distribution of such tables can be classified into three distinct cases. # The row sums n_1, n_0 and column sums s_1, s_0 are fixed in advance and not random. Then all x_ are determined by x_. If A and B are independent, x_ follows a hypergeometric distribution with parameters n, n_1, s_1: x_ \sim \mbox(n, n_1, s_1). # The row sums n_1, n_0 are fixed in advance but the column sums s_1, s_0 are not. Then all random parameters are determined by x_ and x_ and x_, x_ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Hypothesis Testing
A statistical hypothesis test is a method of statistical inference used to decide whether the data at hand sufficiently support a particular hypothesis. Hypothesis testing allows us to make probabilistic statements about population parameters. History Early use While hypothesis testing was popularized early in the 20th century, early forms were used in the 1700s. The first use is credited to John Arbuthnot (1710), followed by Pierre-Simon Laplace (1770s), in analyzing the human sex ratio at birth; see . Modern origins and early controversy Modern significance testing is largely the product of Karl Pearson ( ''p''-value, Pearson's chi-squared test), William Sealy Gosset ( Student's t-distribution), and Ronald Fisher ("null hypothesis", analysis of variance, "significance test"), while hypothesis testing was developed by Jerzy Neyman and Egon Pearson (son of Karl). Ronald Fisher began his life in statistics as a Bayesian (Zabell 1992), but Fisher soon grew disenchanted with t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
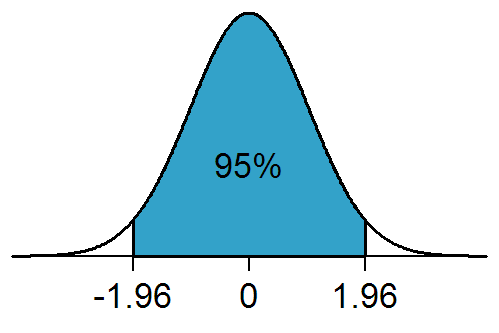
Significance Level
In statistical hypothesis testing, a result has statistical significance when it is very unlikely to have occurred given the null hypothesis (simply by chance alone). More precisely, a study's defined significance level, denoted by \alpha, is the probability of the study rejecting the null hypothesis, given that the null hypothesis is true; and the ''p''-value of a result, ''p'', is the probability of obtaining a result at least as extreme, given that the null hypothesis is true. The result is statistically significant, by the standards of the study, when p \le \alpha. The significance level for a study is chosen before data collection, and is typically set to 5% or much lower—depending on the field of study. In any experiment or observation that involves drawing a sample from a population, there is always the possibility that an observed effect would have occurred due to sampling error alone. But if the ''p''-value of an observed effect is less than (or equal to) the significa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Barnard's Test
In statistics, Barnard’s test is an exact test used in the analysis of contingency tables with one margin fixed. Barnard’s tests are really a class of hypothesis tests, also known as unconditional exact tests for two independent binomials. These tests examine the association of two categorical variables and are often a more powerful alternative than Fisher's exact test for contingency tables. While first published in 1945 by G.A. Barnard, the test did not gain popularity due to the computational difficulty of calculating the value and Fisher’s specious disapproval. Nowadays, for small / moderate sample sizes computers can often implement Barnard’s test in a few seconds. Purpose and scope Barnard’s test is used to test the independence of rows and columns in a contingency table. The test assumes each response is independent. Under independence, there are three types of study designs that yield a table, and Barnard's test applies to the second type. To distingu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
StatXact
StatXact is a statistical software package for analyzing data using exact statistics. It calculates exact p-values and confidence intervals for contingency tables and non-parametric procedures. It is marketed by Cytel Cytel is a multinational statistical software developer and contract research organization, headquartered in Cambridge, Massachusetts, USA. Cytel provides clinical trial design, implementation services, and statistical products primarily for the b ... Inc. References * External links StatXact homepage at Cytel Inc. Statistical software Windows-only software {{statistics-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
R (programming Language)
R is a programming language for statistical computing and graphics supported by the R Core Team and the R Foundation for Statistical Computing. Created by statisticians Ross Ihaka and Robert Gentleman, R is used among data miners, bioinformaticians and statisticians for data analysis and developing statistical software. Users have created packages to augment the functions of the R language. According to user surveys and studies of scholarly literature databases, R is one of the most commonly used programming languages used in data mining. R ranks 12th in the TIOBE index, a measure of programming language popularity, in which the language peaked in 8th place in August 2020. The official R software environment is an open-source free software environment within the GNU package, available under the GNU General Public License. It is written primarily in C, Fortran, and R itself (partially self-hosting). Precompiled executables are provided for various operating systems. R ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
SciPy
SciPy (pronounced "sigh pie") is a free and open-source Python library used for scientific computing and technical computing. SciPy contains modules for optimization, linear algebra, integration, interpolation, special functions, FFT, signal and image processing, ODE solvers and other tasks common in science and engineering. SciPy is also a family of conferences for users and developers of these tools: SciPy (in the United States), EuroSciPy (in Europe) and SciPy.in (in India). Enthought originated the SciPy conference in the United States and continues to sponsor many of the international conferences as well as host the SciPy website. The SciPy library is currently distributed under the BSD license, and its development is sponsored and supported by an open community of developers. It is also supported by NumFOCUS, a community foundation for supporting reproducible and accessible science. Components The SciPy package is at the core of Python's scientific computing capabilit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Confidence Interval
In frequentist statistics, a confidence interval (CI) is a range of estimates for an unknown parameter. A confidence interval is computed at a designated ''confidence level''; the 95% confidence level is most common, but other levels, such as 90% or 99%, are sometimes used. The confidence level represents the long-run proportion of corresponding CIs that contain the true value of the parameter. For example, out of all intervals computed at the 95% level, 95% of them should contain the parameter's true value. Factors affecting the width of the CI include the sample size, the variability in the sample, and the confidence level. All else being the same, a larger sample produces a narrower confidence interval, greater variability in the sample produces a wider confidence interval, and a higher confidence level produces a wider confidence interval. Definition Let be a random sample from a probability distribution with statistical parameter , which is a quantity to be estimate ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Critical Value
Critical value may refer to: *In differential topology, a critical value of a differentiable function between differentiable manifolds is the image (value of) ƒ(''x'') in ''N'' of a critical point ''x'' in ''M''. *In statistical hypothesis testing, the critical values of a statistical test are the boundaries of the acceptance region of the test. The acceptance region is the set of values of the test statistic for which the null hypothesis is not rejected. Depending on the shape of the acceptance region, there can be one or more than one critical value. *In complex dynamics, a critical value Critical value may refer to: *In differential topology, a critical value of a differentiable function between differentiable manifolds is the image (value of) ƒ(''x'') in ''N'' of a critical point ''x'' in ''M''. *In statistical hypothesis ... is the image of a critical point. *In medicine, a critical value or panic value is a value of a laboratory test that indicates a serio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Test Statistic
A test statistic is a statistic (a quantity derived from the sample) used in statistical hypothesis testing.Berger, R. L.; Casella, G. (2001). ''Statistical Inference'', Duxbury Press, Second Edition (p.374) A hypothesis test is typically specified in terms of a test statistic, considered as a numerical summary of a data-set that reduces the data to one value that can be used to perform the hypothesis test. In general, a test statistic is selected or defined in such a way as to quantify, within observed data, behaviours that would distinguish the null from the alternative hypothesis, where such an alternative is prescribed, or that would characterize the null hypothesis if there is no explicitly stated alternative hypothesis. An important property of a test statistic is that its sampling distribution under the null hypothesis must be calculable, either exactly or approximately, which allows ''p''-values to be calculated. A ''test statistic'' shares some of the same qualities o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Decision Rule
In decision theory, a decision rule is a function which maps an observation to an appropriate action. Decision rules play an important role in the theory of statistics and economics, and are closely related to the concept of a strategy (game theory), strategy in game theory. In order to evaluate the usefulness of a decision rule, it is necessary to have a loss function detailing the outcome of each action under different states. Formal definition Given an observable random variable ''X'' over the probability space \scriptstyle (\mathcal,\Sigma, P_\theta), determined by a parameter ''θ'' ∈ ''Θ'', and a set ''A'' of possible actions, a (deterministic) decision rule is a function ''δ'' : \scriptstyle\mathcal→ ''A''. Examples of decision rules * An estimator is a decision rule used for estimating a parameter. In this case the set of actions is the parameter space, and a loss function details the cost of the discrepancy between the true value of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
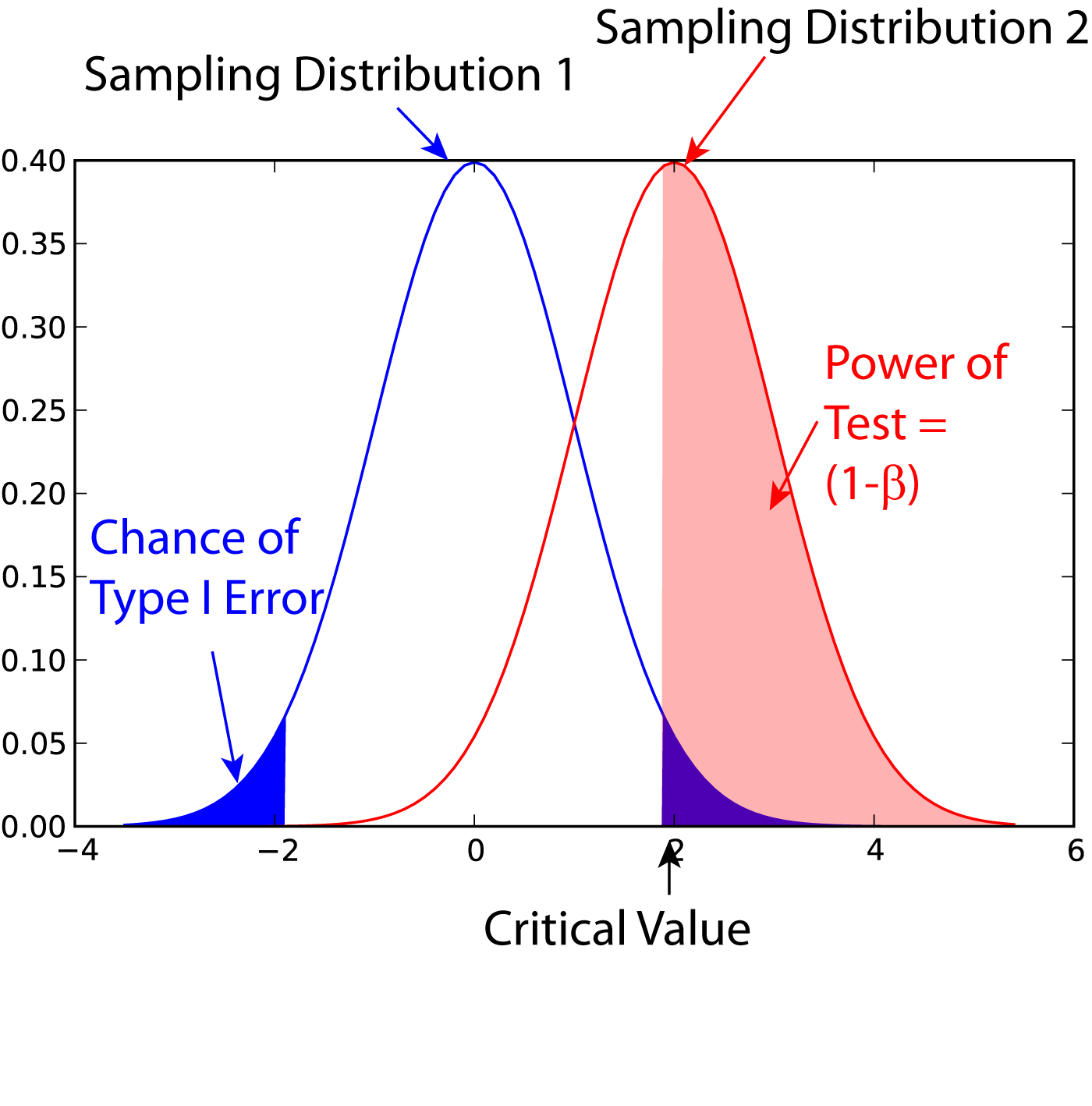
Power (statistics)
In statistics, the power of a binary hypothesis test is the probability that the test correctly rejects the null hypothesis (H_0) when a specific alternative hypothesis (H_1) is true. It is commonly denoted by 1-\beta, and represents the chances of a true positive detection conditional on the actual existence of an effect to detect. Statistical power ranges from 0 to 1, and as the power of a test increases, the probability \beta of making a type II error by wrongly failing to reject the null hypothesis decreases. Notation This article uses the following notation: * ''β'' = probability of a Type II error, known as a "false negative" * 1 − ''β'' = probability of a "true positive", i.e., correctly rejecting the null hypothesis. "1 − ''β''" is also known as the power of the test. * ''α'' = probability of a Type I error, known as a "false positive" * 1 − ''α'' = probability of a "true negative", i.e., correctly not rejecting the null hypothesis Description For a ty ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nuisance Parameter
Nuisance (from archaic ''nocence'', through Fr. ''noisance'', ''nuisance'', from Lat. ''nocere'', "to hurt") is a common law tort. It means that which causes offence, annoyance, trouble or injury. A nuisance can be either public (also "common") or private. A public nuisance was defined by English scholar Sir James Fitzjames Stephen as, "an act not warranted by law, or an omission to discharge a legal duty, which act or omission obstructs or causes inconvenience or damage to the public in the exercise of rights common to all Her Majesty's subjects". ''Private nuisance'' is the interference with the right of specific people. Nuisance is one of the oldest causes of action known to the common law, with cases framed in nuisance going back almost to the beginning of recorded case law. Nuisance signifies that the "right of quiet enjoyment" is being disrupted to such a degree that a tort is being committed. Definition Under the common law, persons in possession of real property (land ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
