|
Blackwell's Contraction Mapping Theorem
In mathematics, Blackwell's contraction mapping theorem provides a set of sufficient conditions for an operator to be a contraction mapping. It is widely used in areas that rely on dynamic programming as it facilitates the proof of existence of fixed points. The result is due to David Blackwell who published it in 1965 in the Annals of Mathematical Statistics. Statement of the Theorem Let T be an operator defined over an ordered normed vector space X. T: X \rightarrow X is a contraction mapping with modulus \beta if it satisfies # (monotonicity) \quad u \leq v \implies Tu \leq Tv # (discounting) \quad T(u+c) \leq Tu+\beta c. Proof of the Theorem For all u and v \in X, u \leq v + , , v-u, , . Properties 1. and 2. imply that T(v) \leq T(u + , , v-u, , ) \leq T(u) + \beta , , v-u, , , hence, T(v)-T(u) \leq \beta , , v-u, , . Therefore , , T(v)-T(u), , \leq \beta , , v-u, , and T is a contraction mapping. Illustration If X is the real line with the usual order ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Contraction Mapping
In mathematics, a contraction mapping, or contraction or contractor, on a metric space (''M'', ''d'') is a function ''f'' from ''M'' to itself, with the property that there is some real number 0 \leq k < 1 such that for all ''x'' and ''y'' in ''M'', : The smallest such value of ''k'' is called the Lipschitz constant of ''f''. Contractive maps are sometimes called Lipschitzian maps. If the above condition is instead satisfied for ''k'' ≤ 1, then the mapping is said to be a non-expansive map. More generally, the idea of a contractive mapping can be defined for maps between metric spaces. Thus, if (''M'', ''d'') and (''N'', ''d) are two metric spaces, then is a contractive mapping if there is a constant such that : |
David Blackwell
David Harold Blackwell (April 24, 1919 – July 8, 2010) was an American statistician and mathematician who made significant contributions to game theory, probability theory, information theory, and statistics. He is one of the eponyms of the Rao–Blackwell theorem, and is also known for the Blackwell channel, Blackwell's contraction mapping theorem, Blackwell's approachability theorem, and the Blackwell order. He was the first African American inducted into the National Academy of Sciences, the first African American full professor with tenure at the University of California, Berkeley, and the seventh African American to receive a Ph.D. in mathematics. In 2012, President Barack Obama posthumously awarded Blackwell the National Medal of Science. Blackwell was also a pioneer in textbook writing. He wrote one of the first Bayesian statistics textbooks, his 1969 ''Basic Statistics''. By the time he retired, he had published over 90 papers and books on dynamic programming, g ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Annals Of Mathematical Statistics
The ''Annals of Mathematical Statistics'' was a peer-reviewed statistics journal published by the Institute of Mathematical Statistics from 1930 to 1972. It was superseded by the '' Annals of Statistics'' and the '' Annals of Probability''. In 1938, Samuel Wilks became editor-in-chief of the ''Annals'' and recruited a remarkable editorial staff: Fisher, Neyman, Cramér, Hotelling, Egon Pearson Egon Sharpe Pearson (11 August 1895 – 12 June 1980) was one of three children of Karl Pearson and Maria, née Sharpe, and, like his father, a British statistician. Career Pearson was educated at Winchester College and Trinity College ..., Georges Darmois, Allen T. Craig, Deming, von Mises, H. L. Rietz, and Shewhart. References External links ''Annals of Mathematical Statistics''at Project Euclid Statistics journals Probability journals {{statistics-journal-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Normed Vector Space
The Ateliers et Chantiers de France (ACF, Workshops and Shipyards of France) was a major shipyard that was established in Dunkirk, France, in 1898. The shipyard boomed in the period before World War I (1914–18), but struggled in the inter-war period. It was badly damaged during World War II (1939–45). In the first thirty years after the war the shipyard again experienced a boom and employed up to 3,000 workers making oil tankers, and then liquid natural gas tankers. Demand dropped off in the 1970s and 1980s. In 1972 the shipyard became Chantiers de France-Dunkerque, and in 1983 merged with others yards to become part of Chantiers du Nord et de la Mediterranee, or Normed. The shipyard closed in 1987. Foundation (1898–99) The Ateliers et Chantiers de France (ACF) company was officially founded on 6 July 1898 by a consortium of six shipping brokers, the Dunkirk chamber of commerce and the state. The state asked that the shipyard be able to build steamships and also four-maste ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
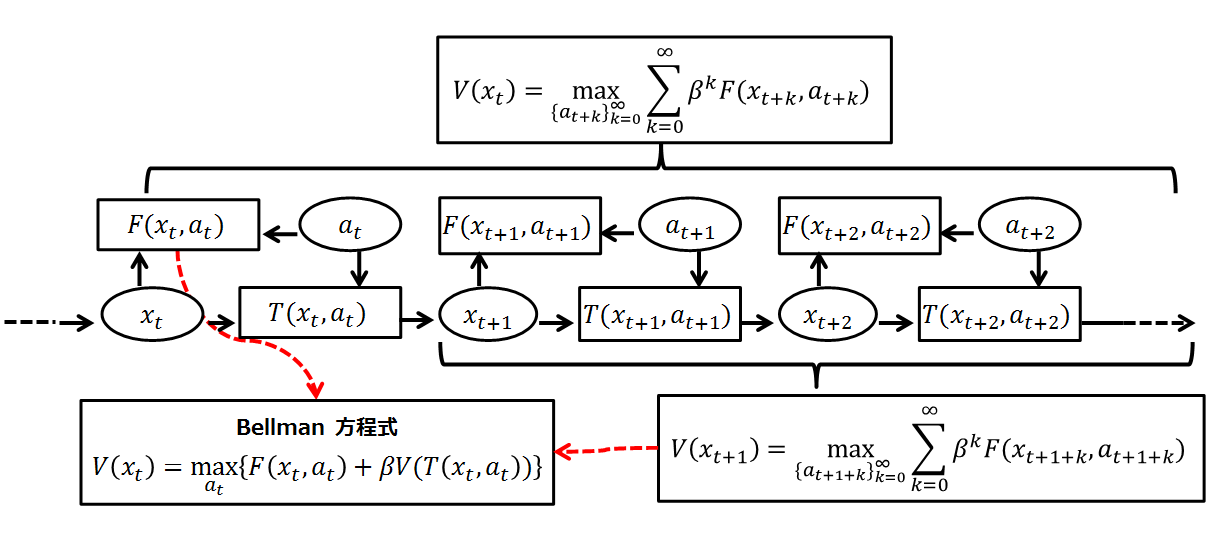
Bellman Equation
A Bellman equation, named after Richard E. Bellman, is a necessary condition for optimality associated with the mathematical Optimization (mathematics), optimization method known as dynamic programming. It writes the "value" of a decision problem at a certain point in time in terms of the payoff from some initial choices and the "value" of the remaining decision problem that results from those initial choices. This breaks a dynamic optimization problem into a sequence of simpler subproblems, as Bellman's “principle of optimality" prescribes. The equation applies to algebraic structures with a total ordering; for algebraic structures with a partial ordering, the generic Bellman's equation can be used. The Bellman equation was first applied to engineering control theory and to other topics in applied mathematics, and subsequently became an important tool in economic theory; though the basic concepts of dynamic programming are prefigured in John von Neumann and Oskar Morgenstern's ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Banach Fixed-point Theorem
In mathematics, the Banach fixed-point theorem (also known as the contraction mapping theorem or contractive mapping theorem or Banach–Caccioppoli theorem) is an important tool in the theory of metric spaces; it guarantees the existence and uniqueness of fixed points of certain self-maps of metric spaces and provides a constructive method to find those fixed points. It can be understood as an abstract formulation of Picard's method of successive approximations. The theorem is named after Stefan Banach (1892–1945) who first stated it in 1922. Statement ''Definition.'' Let (X, d) be a metric space. Then a map T : X \to X is called a contraction mapping on ''X'' if there exists q \in empty complete metric space with a contraction mapping T : X \to X. Then ''T'' admits a unique Fixed point (mathematics)">fixed-point x^* in ''X'' (i.e. T(x^*) = x^*). Furthermore, x^* can be found as follows: start with an arbitrary element x_0 \in X and define a sequence (x_n)_ by x_n = T(x_) for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fixed-point Theorems
In mathematics, a fixed-point theorem is a result saying that a function ''F'' will have at least one fixed point (a point ''x'' for which ''F''(''x'') = ''x''), under some conditions on ''F'' that can be stated in general terms. In mathematical analysis The Banach fixed-point theorem (1922) gives a general criterion guaranteeing that, if it is satisfied, the procedure of iterating a function yields a fixed point. By contrast, the Brouwer fixed-point theorem (1911) is a non- constructive result: it says that any continuous function from the closed unit ball in ''n''-dimensional Euclidean space to itself must have a fixed point, but it doesn't describe how to find the fixed point (see also Sperner's lemma). For example, the cosine function is continuous in ��1, 1and maps it into ��1, 1 and thus must have a fixed point. This is clear when examining a sketched graph of the cosine function; the fixed point occurs where the cosine curve ''y'' = cos(''x'') intersects t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Metric Geometry
In mathematics, a metric space is a Set (mathematics), set together with a notion of ''distance'' between its Element (mathematics), elements, usually called point (geometry), points. The distance is measured by a function (mathematics), function called a metric or distance function. Metric spaces are a general setting for studying many of the concepts of mathematical analysis and geometry. The most familiar example of a metric space is 3-dimensional Euclidean space with its usual notion of distance. Other well-known examples are a sphere equipped with the angular distance and the hyperbolic plane. A metric may correspond to a Conceptual metaphor , metaphorical, rather than physical, notion of distance: for example, the set of 100-character Unicode strings can be equipped with the Hamming distance, which measures the number of characters that need to be changed to get from one string to another. Since they are very general, metric spaces are a tool used in many different bra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |