|
Black's Approximation
In finance, Black's approximation is an approximate method for computing the value of an American call option on a stock paying a single dividend. It was described by Fischer Black in 1975.F. Black: Fact and fantasy in the use of options, FAJ, July–August 1975, pp.36 The Black–Scholes formula (hereinafter, "BS Formula") provides an explicit equation for the value of a call option on a non-dividend paying stock. In case the stock pays one or more discrete dividend(s) no closed formula is known, but several approximations can be used, or else the Black–Scholes PDE will have to be solved numerically. One such approximation is described here. See also Black–Scholes model#American options. The method essentially entails using the BS formula to compute the value of two European call options: (1) A European call with the same maturity as the American call being valued, but with the stock price reduced by the present value of the dividend, and (2) A European call that expires o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Finance
Finance refers to monetary resources and to the study and Academic discipline, discipline of money, currency, assets and Liability (financial accounting), liabilities. As a subject of study, is a field of Business administration, Business Administration wich study the planning, organizing, leading, and controlling of an organization's resources to achieve its goals. Based on the scope of financial activities in financial systems, the discipline can be divided into Personal finance, personal, Corporate finance, corporate, and public finance. In these financial systems, assets are bought, sold, or traded as financial instruments, such as Currency, currencies, loans, Bond (finance), bonds, Share (finance), shares, stocks, Option (finance), options, Futures contract, futures, etc. Assets can also be banked, Investment, invested, and Insurance, insured to maximize value and minimize loss. In practice, Financial risk, risks are always present in any financial action and entities. Due ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fischer Black
Fischer Sheffey Black (January 11, 1938 – August 30, 1995) was an American economist, best known as one of the authors of the Black–Scholes equation. Working variously at the University of Chicago, the Massachusetts Institute of Technology, and at Goldman Sachs, Black died two years before the Nobel Memorial Prize in Economic Sciences (which is not given posthumously) was awarded to his collaborator Myron Scholes and former colleague Robert C. Merton for the Black-Scholes model and Merton's application of the model to a continuous-time framework. Black also made significant contributions to the capital asset pricing model and the theory of accounting, as well as more controversial contributions in monetary economics and the theory of business cycles. Background Fischer Sheffey Black was born on January 11, 1938. He graduated from Harvard College with a major in physics in 1959 and received a PhD in applied mathematics from Harvard University in 1964. He was initially ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Black–Scholes Model
The Black–Scholes or Black–Scholes–Merton model is a mathematical model for the dynamics of a financial market containing Derivative (finance), derivative investment instruments. From the parabolic partial differential equation in the model, known as the Black–Scholes equation, one can deduce the Black–Scholes formula, which gives a theoretical estimate of the price of option style, European-style option (finance), options and shows that the option has a ''unique'' price given the risk of the security and its expected return (instead replacing the security's expected return with the risk-neutral rate). The equation and model are named after economists Fischer Black and Myron Scholes. Robert C. Merton, who first wrote an academic paper on the subject, is sometimes also credited. The main principle behind the model is to hedge (finance), hedge the option by buying and selling the underlying asset in a specific way to eliminate risk. This type of hedging is called "continuou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cumulative Distribution Function
In probability theory and statistics, the cumulative distribution function (CDF) of a real-valued random variable X, or just distribution function of X, evaluated at x, is the probability that X will take a value less than or equal to x. Every probability distribution Support (measure theory), supported on the real numbers, discrete or "mixed" as well as Continuous variable, continuous, is uniquely identified by a right-continuous Monotonic function, monotone increasing function (a càdlàg function) F \colon \mathbb R \rightarrow [0,1] satisfying \lim_F(x)=0 and \lim_F(x)=1. In the case of a scalar continuous distribution, it gives the area under the probability density function from negative infinity to x. Cumulative distribution functions are also used to specify the distribution of multivariate random variables. Definition The cumulative distribution function of a real-valued random variable X is the function given by where the right-hand side represents the probability ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Standard Normal Distribution
In probability theory and statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is f(x) = \frac e^\,. The parameter is the mean or expectation of the distribution (and also its median and mode), while the parameter \sigma^2 is the variance. The standard deviation of the distribution is (sigma). A random variable with a Gaussian distribution is said to be normally distributed, and is called a normal deviate. Normal distributions are important in statistics and are often used in the natural and social sciences to represent real-valued random variables whose distributions are not known. Their importance is partly due to the central limit theorem. It states that, under some conditions, the average of many samples (observations) of a random variable with finite mean and variance is itself a random variable—whose distribution conver ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Risk-free Interest Rate
The risk-free rate of return, usually shortened to the risk-free rate, is the rate of return of a hypothetical investment with scheduled payments over a fixed period of time that is assumed to meet all payment obligations. Since the risk-free rate can be obtained with no risk, any other investment having some risk will have to have a higher rate of return in order to induce any investors to hold it. In practice, to infer the risk-free interest rate in a particular currency, market participants often choose the yield to maturity on a risk-free bond issued by a government of the same currency whose risks of default are so low as to be negligible. For example, the rate of return on zero-coupon Treasury bonds (T-bills) is sometimes seen as the risk-free rate of return in US dollars. Theoretical measurement As stated by Malcolm Kemp in chapter five of his book ''Market Consistency: Model Calibration in Imperfect Markets'', the risk-free rate means different things to different pe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continuous Compounding
Compound interest is interest accumulated from a principal sum and previously accumulated interest. It is the result of reinvesting or retaining interest that would otherwise be paid out, or of the accumulation of debts from a borrower. Compound interest is contrasted with simple interest, where previously accumulated interest is not added to the principal amount of the current period. Compounded interest depends on the simple interest rate applied and the frequency at which the interest is compounded. Compounding frequency The ''compounding frequency'' is the number of times per given unit of time the accumulated interest is capitalized, on a regular basis. The frequency could be yearly, half-yearly, quarterly, monthly, weekly, daily, continuously, or not at all until maturity. For example, monthly capitalization with interest expressed as an annual rate means that the compounding frequency is 12, with time periods measured in months. Annual equivalent rate To help consum ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
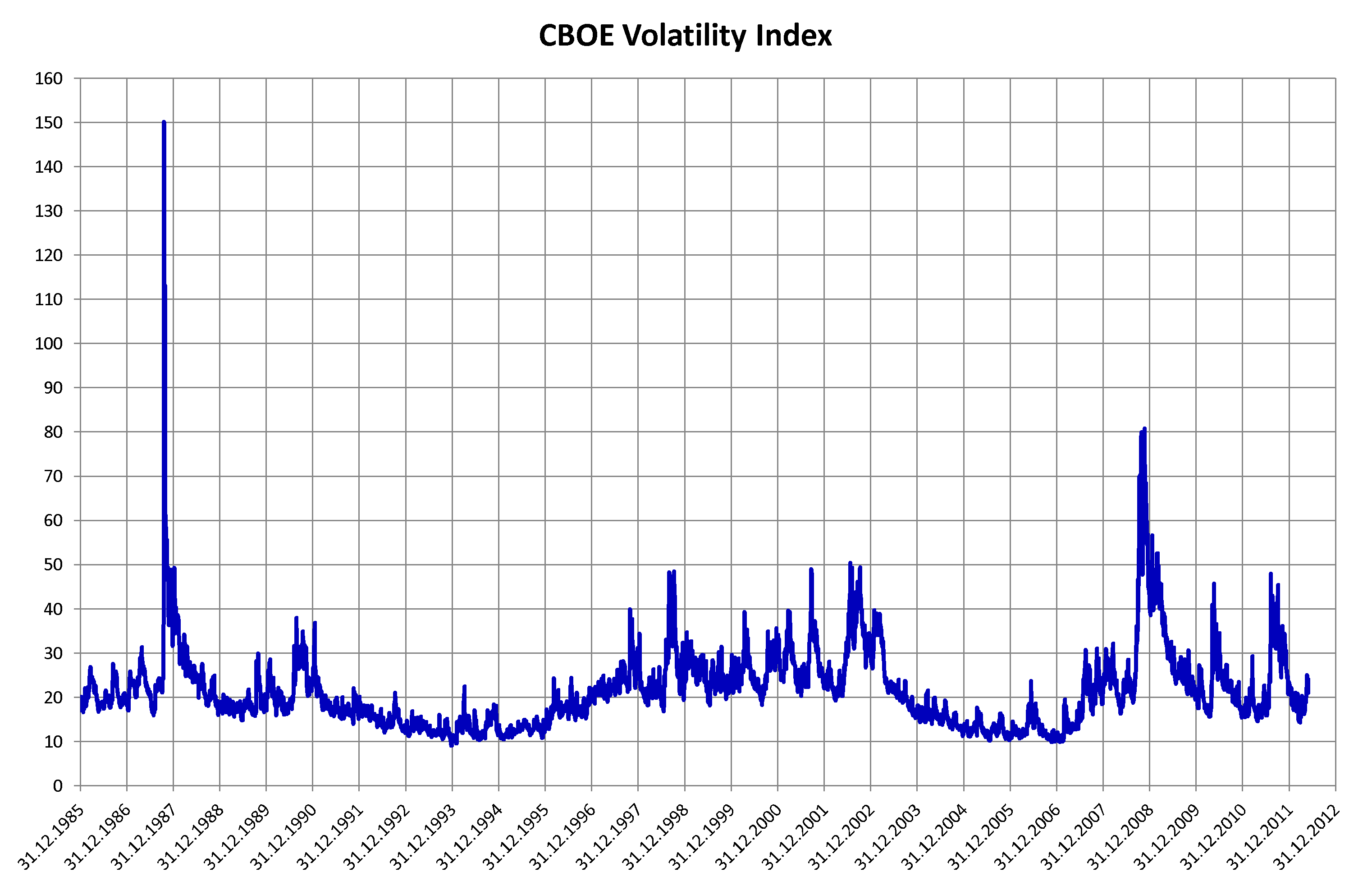
Volatility (finance)
In finance, volatility (usually denoted by "sigma, σ") is the Variability (statistics), degree of variation of a trading price series over time, usually measured by the standard deviation of logarithmic returns. Historic volatility measures a time series of past market prices. Implied volatility looks forward in time, being derived from the market price of a market-traded derivative (in particular, an option). Volatility terminology Volatility as described here refers to the actual volatility, more specifically: * actual current volatility of a financial instrument for a specified period (for example 30 days or 90 days), based on historical prices over the specified period with the last observation the most recent price. * actual historical volatility which refers to the volatility of a financial instrument over a specified period but with the last observation on a date in the past **near synonymous is realized volatility, the square root of the realized variance, in turn c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Financial Models
An economic model is a theoretical construct representing economic processes by a set of variables and a set of logical and/or quantitative relationships between them. The economic model is a simplified, often mathematical, framework designed to illustrate complex processes. Frequently, economic models posit structural parameters. A model may have various exogenous variables, and those variables may change to create various responses by economic variables. Methodological uses of models include investigation, theorizing, and fitting theories to the world. Overview In general terms, economic models have two functions: first as a simplification of and abstraction from observed data, and second as a means of selection of data based on a paradigm of econometric study. ''Simplification'' is particularly important for economics given the enormous complexity of economic processes. This complexity can be attributed to the diversity of factors that determine economic activity; the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |