|
Birge–Sponer Method
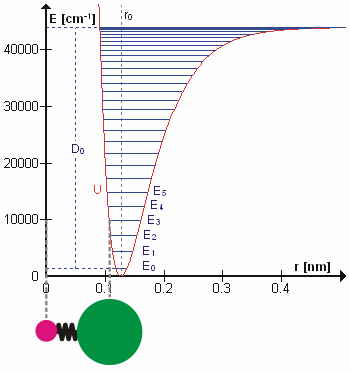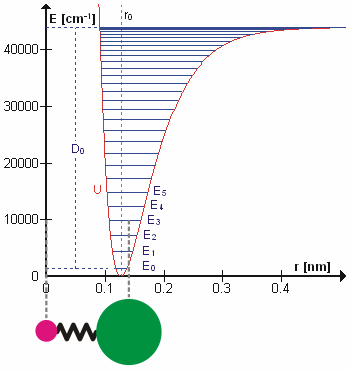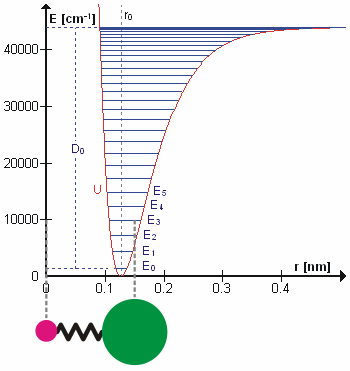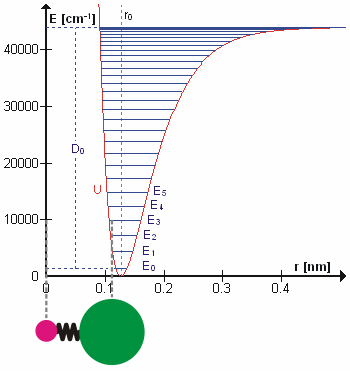
In molecular spectroscopy, the Birge–Sponer method or Birge–Sponer plot is a way to calculate the dissociation energy of a molecule. This method takes its name from Raymond Thayer Birge and Hertha Sponer, the two physical chemists that developed it. A detailed example may be found here.David, Carl W., "The Birge Sponer Extrapolation" (2008). Chemistry Education Materials. Paper 63. http://digitalcommons.uconn.edu/chem_educ/63 Description By observing transitions between as many vibrational energy levels as possible, for example through electronic or infrared spectroscopy, the difference between the energy levels, \Delta G_=G(v+1)-G(v) can be calculated. This sum will have a maximum at v_, representing the point of bond dissociation; summing over all the differences up to this point gives the total energy required to dissociate the molecule, i.e. to promote it from the ground state to an unbound state. This can be written: :D_0=\sum_^ \Delta G_ where D_0 is the dissociation en ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spectroscopy
Spectroscopy is the field of study that measures and interprets electromagnetic spectra. In narrower contexts, spectroscopy is the precise study of color as generalized from visible light to all bands of the electromagnetic spectrum. Spectroscopy, primarily in the electromagnetic spectrum, is a fundamental exploratory tool in the fields of astronomy, chemistry, materials science, and physics, allowing the composition, physical structure and electronic structure of matter to be investigated at the atomic, molecular and macro scale, and over astronomical distances. Historically, spectroscopy originated as the study of the wavelength dependence of the absorption by gas phase matter of visible light dispersed by a prism. Current applications of spectroscopy include biomedical spectroscopy in the areas of tissue analysis and medical imaging. Matter waves and acoustic waves can also be considered forms of radiative energy, and recently gravitational waves have been associa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dissociation Energy
The bond-dissociation energy (BDE, ''D''0, or ''DH°'') is one measure of the strength of a chemical bond . It can be defined as the standard enthalpy change when is cleaved by homolysis to give fragments A and B, which are usually radical species. The enthalpy change is temperature-dependent, and the bond-dissociation energy is often defined to be the enthalpy change of the homolysis at 0 K (absolute zero), although the enthalpy change at 298 K (standard conditions) is also a frequently encountered parameter. As a typical example, the bond-dissociation energy for one of the C−H bonds in ethane () is defined as the standard enthalpy change of the process : , : ''DH''°298() = Δ''H°'' = 101.1(4) kcal/mol = 423.0 ± 1.7 kJ/mol = 4.40(2) eV (per bond). To convert a molar BDE to the energy needed to dissociate the bond ''per molecule'', the conversion factor 23.060 kcal/mol (96.485 kJ/mol) for each eV can be used. A variety of experimen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Raymond Thayer Birge
Raymond Thayer Birge (March 13, 1887 – March 22, 1980) was an American physicist. Career Born in Brooklyn, New York, into a family of academic scientists, Birge obtained his doctorate from the University of Wisconsin in 1913. In the same year he married Irene A. Walsh. The Birges had two children, Carolyn Elizabeth (Mrs. E. D. Yocky) and Robert Walsh, Associate Director of the Lawrence Berkeley National Laboratory in 1973-1981. After five years as an instructor at Syracuse University, he became a member of the physics department at University of California, Berkeley, where he remained until he retired, as chairman, in 1955. On his arrival at Berkeley, Birge sought collaboration with the Berkeley College of Chemistry, then under the leadership of Gilbert N. Lewis. However, Birge's championing of the Bohr atom led him into conflict with the chemists who defended Lewis' earlier theory of the cubical atom. Birge was unafraid of scientific controversy and persevered with his cou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hertha Sponer
Hertha Sponer (1 September 1895 – 27 February 1968) was a German physicist and chemist who contributed to modern quantum mechanics and molecular physics and was the first woman on the physics faculty of Duke University. She was the older sister of philologist and resistance fighter Margot Sponer. Life and career Sponer was born in Neisse (Nysa), Prussian Silesia, and obtained her high school degree in Neisse. She spent a year at the University of Tübingen, after which she enrolled at the University of Göttingen where she received her PhD in 1920 under the supervision of Peter Debye. During her time at the University of Tübingen, she was an assistant of James Franck. In 1921 she, along with a few others, was among the first women to obtain a PhD in physics in Germany along with the right to teach science at a German university. In October 1925 she received a Rockefeller Foundation fellowship to stay at University of California, Berkeley, where she remained for a year. Durin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Molecular Vibration
A molecular vibration is a Periodic function, periodic motion of the atoms of a molecule relative to each other, such that the center of mass of the molecule remains unchanged. The infrared spectroscopy correlation table, typical vibrational frequencies range from less than 1013 hertz, Hz to approximately 1014 Hz, corresponding to wavenumbers of approximately 300 to 3000 cm−1 and wavelengths of approximately 30 to 3 μm. Vibrations of polyatomic molecules are described in terms of normal modes, which are independent of each other, but each normal mode involves simultaneous vibrations of parts of the molecule. In general, a non-linear molecule with ''N'' atoms has vibrational mode, normal modes of vibration, but a ''linear'' molecule has modes, because rotation about the molecular axis cannot be observed. A diatomic molecule has one normal mode of vibration, since it can only stretch or compress the single bond. A molecular vibration is excited when the mo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Infrared Spectroscopy
Infrared spectroscopy (IR spectroscopy or vibrational spectroscopy) is the measurement of the interaction of infrared radiation with matter by absorption, emission, or reflection. It is used to study and identify chemical substances or functional groups in solid, liquid, or gaseous forms. It can be used to characterize new materials or identify and verify known and unknown samples. The method or technique of infrared spectroscopy is conducted with an instrument called an infrared spectrometer (or spectrophotometer) which produces an infrared spectrum. An IR spectrum can be visualized in a graph of infrared light absorbance (or transmittance) on the vertical axis vs. frequency, wavenumber or wavelength on the horizontal axis. Typical units of wavenumber used in IR spectra are reciprocal centimeters, with the symbol cm−1. Units of IR wavelength are commonly given in micrometers (formerly called "microns"), symbol μm, which are related to the wavenumber in a reciprocal way ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Maximum
In mathematical analysis, the maximum and minimum of a function (mathematics), function are, respectively, the greatest and least value taken by the function. Known generically as extremum, they may be defined either within a given Interval (mathematics), range (the ''local'' or ''relative'' extrema) or on the entire domain of a function, domain (the ''global'' or ''absolute'' extrema) of a function. Pierre de Fermat was one of the first mathematicians to propose a general technique, adequality, for finding the maxima and minima of functions. As defined in set theory, the maximum and minimum of a set (mathematics), set are the greatest and least elements in the set, respectively. Unbounded infinite sets, such as the set of real numbers, have no minimum or maximum. In statistics, the corresponding concept is the sample maximum and minimum. Definition A real-valued Function (mathematics), function ''f'' defined on a Domain of a function, domain ''X'' has a global (or absolute) m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ground State
The ground state of a quantum-mechanical system is its stationary state of lowest energy; the energy of the ground state is known as the zero-point energy of the system. An excited state is any state with energy greater than the ground state. In quantum field theory, the ground state is usually called the vacuum. If more than one ground state exists, they are said to be degenerate. Many systems have degenerate ground states. Degeneracy occurs whenever there exists a unitary operator that acts non-trivially on a ground state and commutes with the Hamiltonian of the system. According to the third law of thermodynamics, a system at absolute zero temperature exists in its ground state; thus, its entropy is determined by the degeneracy of the ground state. Many systems, such as a perfect crystal lattice, have a unique ground state and therefore have zero entropy at absolute zero. It is also possible for the highest excited state to have absolute zero temperature for sys ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Morse Potential
The Morse potential, named after physicist Philip M. Morse, is a convenient Interatomic potential, interatomic interaction model for the potential energy of a diatomic molecule. It is a better approximation for the oscillation, vibrational structure of the molecule than the quantum harmonic oscillator because it explicitly includes the effects of bond breaking, such as the existence of unbound states. It also accounts for the anharmonicity of real bonds and the non-zero transition probability for overtone band, overtone and Hot band#Combination bands, combination bands. The Morse potential can also be used to model other interactions such as the interaction between an atom and a surface. Due to its simplicity (only three fitting parameters), it is not used in modern spectroscopy. However, its mathematical form inspired the MLR (Morse/Long-range potential, Morse/Long-range) potential, which is the most popular potential energy function used for fitting spectroscopic data. Potential ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zero Of A Function
In mathematics, a zero (also sometimes called a root) of a real-, complex-, or generally vector-valued function f, is a member x of the domain of f such that f(x) ''vanishes'' at x; that is, the function f attains the value of 0 at x, or equivalently, x is a solution to the equation f(x) = 0. A "zero" of a function is thus an input value that produces an output of 0. A root of a polynomial is a zero of the corresponding polynomial function. The fundamental theorem of algebra shows that any non-zero polynomial has a number of roots at most equal to its degree, and that the number of roots and the degree are equal when one considers the complex roots (or more generally, the roots in an algebraically closed extension) counted with their multiplicities. For example, the polynomial f of degree two, defined by f(x)=x^2-5x+6=(x-2)(x-3) has the two roots (or zeros) that are 2 and 3. f(2)=2^2-5\times 2+6= 0\textf(3)=3^2-5\times 3+6=0. If the function maps real numbers to real n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Franck–Condon Principle
The Franck–Condon principle describes the intensities of vibronic transitions, or the absorption or emission of a photon. It states that when a molecule is undergoing an electronic transition, such as ionization, the nuclear configuration of the molecule experiences no significant change. Overview The Franck–Condon principle has a well-established semiclassical interpretation based on the original contributions of James Franck. Electronic transitions are relatively instantaneous compared with the time scale of nuclear motions, therefore if the molecule is to move to a new vibrational level during the electronic transition, this new vibrational level must be instantaneously compatible with the nuclear positions and momenta of the vibrational level of the molecule in the originating electronic state. In the semiclassical picture of vibrations (oscillations) of a simple harmonic oscillator, the necessary conditions can occur at the turning points, where the momentum is zer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Extrapolation
In mathematics Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ..., extrapolation is a type of estimation, beyond the original observation range, of the value of a variable on the basis of its relationship with another variable. It is similar to interpolation, which produces estimates between known observations, but extrapolation is subject to greater uncertainty and a higher risk of producing meaningless results. Extrapolation may also mean extension of a wikt:method, method, assuming similar methods will be applicable. Extrapolation may also apply to human experience to project, extend, or expand known experience into an area not known or previously experienced. By doing so, one makes an assumption of the unknown [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |