|
Birectified Tesseractic Honeycomb
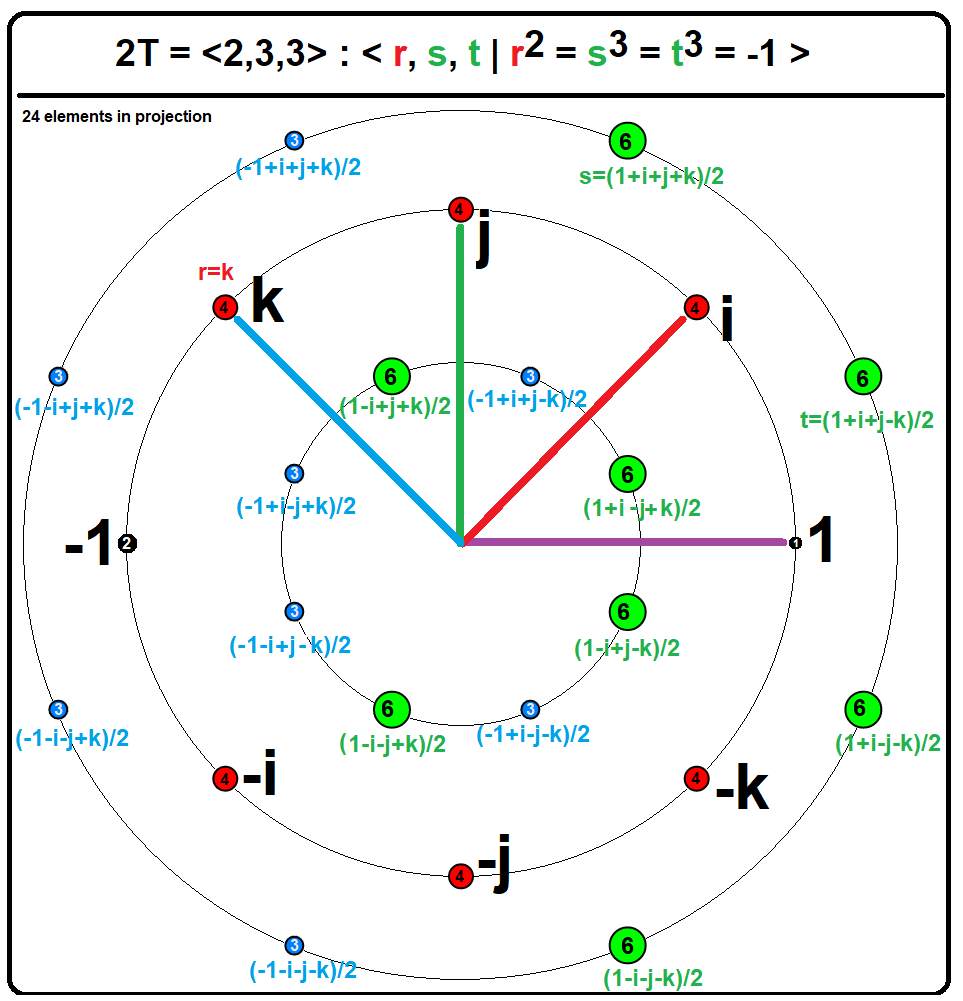
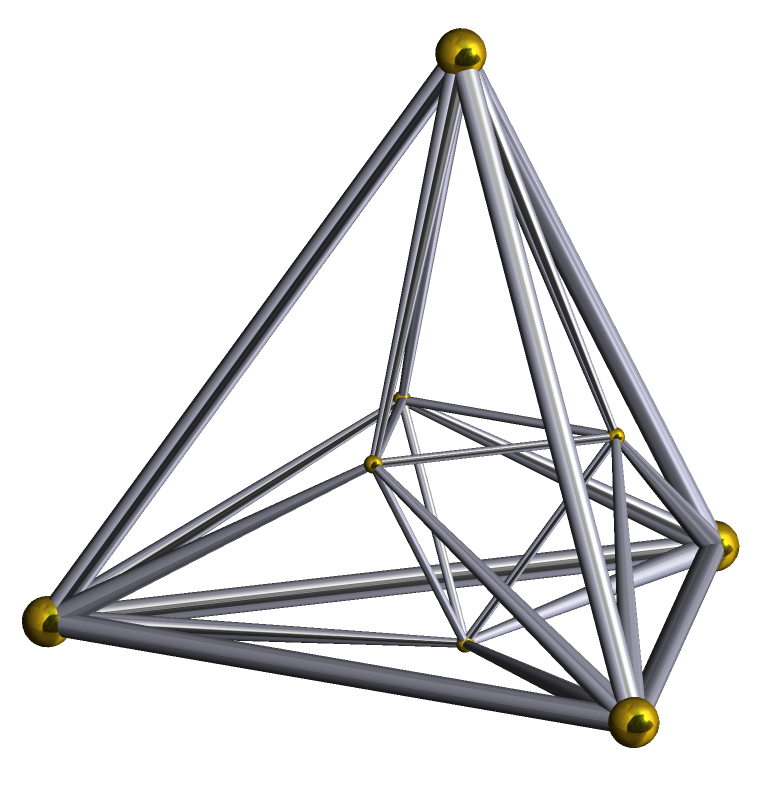
In four-dimensional Euclidean geometry, the 24-cell honeycomb, or icositetrachoric honeycomb is a regular space-filling tessellation (or honeycomb) of 4-dimensional Euclidean space by regular 24-cells. It can be represented by Schläfli symbol . The dual tessellation by regular 16-cell honeycomb has Schläfli symbol . Together with the tesseractic honeycomb (or 4-cubic honeycomb) these are the only regular tessellations of Euclidean 4-space. Coordinates The 24-cell honeycomb can be constructed as the Voronoi tessellation of the D4 or F4 root lattice. Each 24-cell is then centered at a D4 lattice point, i.e. one of :\left\. These points can also be described as Hurwitz quaternions with even square norm. The vertices of the honeycomb lie at the deep holes of the D4 lattice. These are the Hurwitz quaternions with odd square norm. It can be constructed as a birectified tesseractic honeycomb, by taking a tesseractic honeycomb and placing vertices at the centers of all ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Icositetrachoronic Tetracomb
In Four-dimensional space, four-dimensional Euclidean geometry, the 24-cell honeycomb, or icositetrachoric honeycomb is a regular polytope, regular space-filling tessellation (or honeycomb (geometry), honeycomb) of 4-dimensional Euclidean space by regular 24-cells. It can be represented by Schläfli symbol . The dual polytope, dual tessellation by regular 16-cell honeycomb has Schläfli symbol . Together with the tesseractic honeycomb (or 4-cubic honeycomb) these are the only regular tessellations of Euclidean 4-space. Coordinates The 24-cell honeycomb can be constructed as the Voronoi tessellation of the D4 or F4 lattice, F4 root lattice. Each 24-cell is then centered at a D4 lattice point, i.e. one of :\left\. These points can also be described as Hurwitz quaternions with even square norm. The vertices of the honeycomb lie at the deep holes of the D4 lattice. These are the Hurwitz quaternions with odd square norm. It can be constructed as a #Symmetry constructions, birecti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Geometry
Euclidean geometry is a mathematical system attributed to ancient Greek mathematics, Greek mathematician Euclid, which he described in his textbook on geometry: the ''Euclid's Elements, Elements''. Euclid's approach consists in assuming a small set of intuitively appealing axioms (postulates) and deducing many other propositions (theorems) from these. Although many of Euclid's results had been stated earlier,. Euclid was the first to organize these propositions into a logic, logical system in which each result is ''mathematical proof, proved'' from axioms and previously proved theorems. The ''Elements'' begins with plane geometry, still taught in secondary school (high school) as the first axiomatic system and the first examples of mathematical proofs. It goes on to the solid geometry of three dimensions. Much of the ''Elements'' states results of what are now called algebra and number theory, explained in geometrical language. For more than two thousand years, the adjective " ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Edge Figure
In geometry, a vertex figure, broadly speaking, is the figure exposed when a corner of a polyhedron or polytope is sliced off. Definitions Take some corner or vertex of a polyhedron. Mark a point somewhere along each connected edge. Draw lines across the connected faces, joining adjacent points around the face. When done, these lines form a complete circuit, i.e. a polygon, around the vertex. This polygon is the vertex figure. More precise formal definitions can vary quite widely, according to circumstance. For example Coxeter (e.g. 1948, 1954) varies his definition as convenient for the current area of discussion. Most of the following definitions of a vertex figure apply equally well to infinite tilings or, by extension, to space-filling tessellation with polytope cells and other higher-dimensional polytopes. As a flat slice Make a slice through the corner of the polyhedron, cutting through all the edges connected to the vertex. The cut surface is the vertex figure. This ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vertex Figure
In geometry, a vertex figure, broadly speaking, is the figure exposed when a corner of a polyhedron or polytope is sliced off. Definitions Take some corner or Vertex (geometry), vertex of a polyhedron. Mark a point somewhere along each connected edge. Draw lines across the connected faces, joining adjacent points around the face. When done, these lines form a complete circuit, i.e. a polygon, around the vertex. This polygon is the vertex figure. More precise formal definitions can vary quite widely, according to circumstance. For example Coxeter (e.g. 1948, 1954) varies his definition as convenient for the current area of discussion. Most of the following definitions of a vertex figure apply equally well to infinite tessellation, tilings or, by extension, to Honeycomb (geometry), space-filling tessellation with polytope Cell (geometry), cells and other higher-dimensional polytopes. As a flat slice Make a slice through the corner of the polyhedron, cutting through all the edges ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Symmetry Constructions
Symmetry (from grc, συμμετρία "agreement in dimensions, due proportion, arrangement") in everyday language refers to a sense of harmonious and beautiful proportion and balance. In mathematics, "symmetry" has a more precise definition, and is usually used to refer to an object that is invariant under some transformations; including translation, reflection, rotation or scaling. Although these two meanings of "symmetry" can sometimes be told apart, they are intricately related, and hence are discussed together in this article. Mathematical symmetry may be observed with respect to the passage of time; as a spatial relationship; through geometric transformations; through other kinds of functional transformations; and as an aspect of abstract objects, including theoretic models, language, and music. This article describes symmetry from three perspectives: in mathematics, including geometry, the most familiar type of symmetry for many people; in science and nature; and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hurwitz Quaternion
In mathematics, a Hurwitz quaternion (or Hurwitz integer) is a quaternion whose components are ''either'' all integers ''or'' all half-integers (halves of odd integers; a mixture of integers and half-integers is excluded). The set of all Hurwitz quaternions is :H = \left\. That is, either ''a'', ''b'', ''c'', ''d'' are all integers, or they are all half-integers. ''H'' is closed under quaternion multiplication and addition, which makes it a subring of the ring of all quaternions H. Hurwitz quaternions were introduced by . A Lipschitz quaternion (or Lipschitz integer) is a quaternion whose components are all integers. The set of all Lipschitz quaternions :L = \left\ forms a subring of the Hurwitz quaternions ''H''. Hurwitz integers have the advantage over Lipschitz integers that it is possible to perform Euclidean division on them, obtaining a small remainder. Both the Hurwitz and Lipschitz quaternions are examples of noncommutative domains which are not division rings. Struct ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
F4 Lattice
In mathematics, F4 is the name of a Lie group and also its Lie algebra f4. It is one of the five exceptional simple Lie groups. F4 has rank 4 and dimension 52. The compact form is simply connected and its outer automorphism group is the trivial group. Its fundamental representation is 26-dimensional. The compact real form of F4 is the isometry group of a 16-dimensional Riemannian manifold known as the octonionic projective plane OP2. This can be seen systematically using a construction known as the ''magic square'', due to Hans Freudenthal and Jacques Tits. There are 3 real forms: a compact one, a split one, and a third one. They are the isometry groups of the three real Albert algebras. The F4 Lie algebra may be constructed by adding 16 generators transforming as a spinor to the 36-dimensional Lie algebra so(9), in analogy with the construction of E8. In older books and papers, F4 is sometimes denoted by E4. Algebra Dynkin diagram The Dynkin diagram for F4 is: . ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Voronoi Tessellation
Voronoi or Voronoy is a Slavic masculine surname; its feminine counterpart is Voronaya. It may refer to *Georgy Voronoy (1868–1908), Russian and Ukrainian mathematician **Voronoi diagram **Weighted Voronoi diagram ** Voronoi deformation density **Voronoi formula **Voronoi pole In geometry, the positive and negative Voronoi poles of a cell in a Voronoi diagram are certain vertices of the diagram. Definition Let V be the Voronoi diagram for a set of sites P, and let V_p be the Voronoi cell of V corresponding to a site ... ** Centroidal Voronoi tessellation {{Disambiguation, surname ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tesseractic Honeycomb
In four-dimensional euclidean geometry, the tesseractic honeycomb is one of the three regular space-filling tessellations (or honeycombs), represented by Schläfli symbol , and constructed by a 4-dimensional packing of tesseract facets. Its vertex figure is a 16-cell. Two tesseracts meet at each cubic cell, four meet at each square face, eight meet on each edge, and sixteen meet at each vertex. It is an analog of the square tiling, , of the plane and the cubic honeycomb, , of 3-space. These are all part of the hypercubic honeycomb family of tessellations of the form . Tessellations in this family are Self-dual. Coordinates Vertices of this honeycomb can be positioned in 4-space in all integer coordinates (i,j,k,l). Sphere packing Like all regular hypercubic honeycombs, the tesseractic honeycomb corresponds to a sphere packing of edge-length-diameter spheres centered on each vertex, or (dually) inscribed in each cell instead. In the hypercubic honeycomb of 4 dimensions, verte ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
16-cell Honeycomb
In Four-dimensional space, four-dimensional Euclidean geometry, the 16-cell honeycomb is one of the three regular space-filling tessellations (or honeycomb (geometry), honeycombs), represented by Schläfli symbol , and constructed by a 4-dimensional packing of 16-cell Facet (mathematics), facets, three around every face. Its dual is the 24-cell honeycomb. Its vertex figure is a 24-cell. The vertex arrangement is called the B4, D4, or F4 (mathematics)#F4 lattice, F4 lattice. Alternate names * Hexadecachoric tetracomb/honeycomb * Demitesseractic tetracomb/honeycomb Coordinates Vertices can be placed at all integer coordinates (i,j,k,l), such that the sum of the coordinates is even. D4 lattice The vertex arrangement of the 16-cell honeycomb is called the D4 lattice, D4 lattice or F4 lattice. The vertices of this lattice are the centers of the 3-spheres in the densest known sphere packing, packing of equal spheres in 4-space; its kissing number is 24, which is also the same as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dual Polytope
In geometry, every polyhedron is associated with a second dual structure, where the Vertex (geometry), vertices of one correspond to the Face (geometry), faces of the other, and the edges between pairs of vertices of one correspond to the edges between pairs of faces of the other. Such dual figures remain combinatorial or Abstract polytope, abstract polyhedra, but not all can also be constructed as geometric polyhedra. Starting with any given polyhedron, the dual of its dual is the original polyhedron. Duality preserves the Symmetry, symmetries of a polyhedron. Therefore, for many classes of polyhedra defined by their symmetries, the duals belong to a corresponding symmetry class. For example, the regular polyhedrathe (convex) Platonic solids and (star) Kepler–Poinsot polyhedraform dual pairs, where the regular tetrahedron is #Self-dual polyhedra, self-dual. The dual of an Isogonal figure, isogonal polyhedron (one in which any two vertices are equivalent under symmetries of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, that is, in Euclid's Elements, Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are Euclidean spaces of any positive integer dimension (mathematics), dimension, including the three-dimensional space and the ''Euclidean plane'' (dimension two). The qualifier "Euclidean" is used to distinguish Euclidean spaces from other spaces that were later considered in physics and modern mathematics. Ancient History of geometry#Greek geometry, Greek geometers introduced Euclidean space for modeling the physical space. Their work was collected by the Greek mathematics, ancient Greek mathematician Euclid in his ''Elements'', with the great innovation of ''mathematical proof, proving'' all properties of the space as theorems, by starting from a few fundamental properties, called ''postulates'', which either were considered as eviden ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |