|
Bessel Potential
In mathematics, the Bessel potential is a potential (named after Friedrich Wilhelm Bessel) similar to the Riesz potential but with better decay properties at infinity. If ''s'' is a complex number with positive real part then the Bessel potential of order ''s'' is the operator :(I-\Delta)^ where Δ is the Laplace operator and the fractional power is defined using Fourier transforms. Yukawa potentials are particular cases of Bessel potentials for s=2 in the 3-dimensional space. Representation in Fourier space The Bessel potential acts by multiplication on the Fourier transforms: for each \xi \in \mathbb^d : \mathcal((I-\Delta)^ u) (\xi)= \frac. Integral representations When s > 0, the Bessel potential on \mathbb^d can be represented by :(I - \Delta)^ u = G_s \ast u, where the Bessel kernel G_s is defined for x \in \mathbb^d \setminus \ by the integral formula : G_s (x) = \frac \int_0^\infty \frac\,\mathrmy. Here \Gamma denotes the Gamma function. The Bess ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting poin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fractional Integration
In fractional calculus, an area of mathematical analysis, the differintegral (sometime also called the derivigral) is a combined differentiation/integration operator. Applied to a function ƒ, the ''q''-differintegral of ''f'', here denoted by :\mathbb^q f is the fractional derivative (if ''q'' > 0) or fractional integral (if ''q'' So, \frac = \mathcal^\left\ which generalizes to \mathbb^qf(t) = \mathcal^\left\. Under the bilateral Laplace transform, here denoted by \mathcal and defined as \mathcal (t)=\int_^\infty e^ f(t)\, dt, differentiation transforms into a multiplication \mathcal\left frac\right= s\mathcal (t) Generalizing to arbitrary order and solving for \mathbb^qf(t), one obtains \mathbb^qf(t)=\mathcal^\left\. Representation via Newton series is the Newton interpolation over consecutive integer orders: \mathbb^qf(t) =\sum_^ \binom m \sum_^m\binom mk(-1)^f^(x). For fractional derivative definitions described in this section, the following identities hold: : ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Differential Equations
In mathematics, a partial differential equation (PDE) is an equation which imposes relations between the various partial derivatives of a multivariable function. The function is often thought of as an "unknown" to be solved for, similarly to how is thought of as an unknown number to be solved for in an algebraic equation like . However, it is usually impossible to write down explicit formulas for solutions of partial differential equations. There is, correspondingly, a vast amount of modern mathematical and scientific research on methods to numerically approximate solutions of certain partial differential equations using computers. Partial differential equations also occupy a large sector of pure mathematical research, in which the usual questions are, broadly speaking, on the identification of general qualitative features of solutions of various partial differential equations, such as existence, uniqueness, regularity, and stability. Among the many open questions are the e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
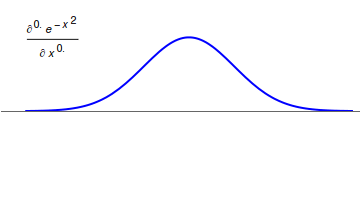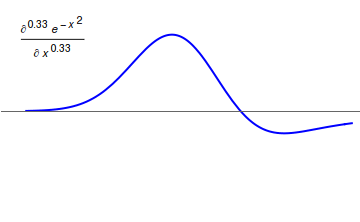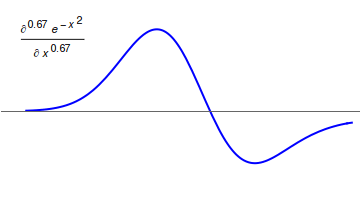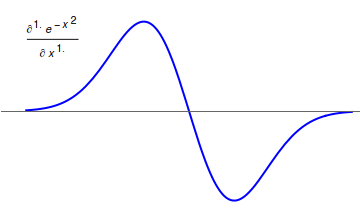
Fractional Calculus
Fractional calculus is a branch of mathematical analysis that studies the several different possibilities of defining real number powers or complex number powers of the differentiation operator D :D f(x) = \frac f(x)\,, and of the integration operator J The symbol J is commonly used instead of the intuitive I in order to avoid confusion with other concepts identified by similar I–like glyphs, such as identities. :J f(x) = \int_0^x f(s) \,ds\,, and developing a calculus for such operators generalizing the classical one. In this context, the term ''powers'' refers to iterative application of a linear operator D to a function f, that is, repeatedly composing D with itself, as in D^n(f) = (\underbrace_n)(f) = \underbrace_n (f)\cdots))). For example, one may ask for a meaningful interpretation of :\sqrt = D^\frac12 as an analogue of the functional square root for the differentiation operator, that is, an expression for some linear operator that, when applied ''twice'' to an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Princeton University Press
Princeton University Press is an independent Academic publishing, publisher with close connections to Princeton University. Its mission is to disseminate scholarship within academia and society at large. The press was founded by Whitney Darrow, with the financial support of Charles Scribner II, Charles Scribner, as a printing press to serve the Princeton community in 1905. Its distinctive building was constructed in 1911 on William Street in Princeton. Its first book was a new 1912 edition of John Witherspoon's ''Lectures on Moral Philosophy.'' History Princeton University Press was founded in 1905 by a recent Princeton graduate, Whitney Darrow, with financial support from another Princetonian, Charles Scribner II. Darrow and Scribner purchased the equipment and assumed the operations of two already existing local publishers, that of the ''Princeton Alumni Weekly'' and the Princeton Press. The new press printed both local newspapers, university documents, ''The Daily Princetonian ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graduate Texts In Mathematics
Graduate Texts in Mathematics (GTM) ( ISSN 0072-5285) is a series of graduate-level textbooks in mathematics published by Springer-Verlag. The books in this series, like the other Springer-Verlag mathematics series, are yellow books of a standard size (with variable numbers of pages). The GTM series is easily identified by a white band at the top of the book. The books in this series tend to be written at a more advanced level than the similar Undergraduate Texts in Mathematics series, although there is a fair amount of overlap between the two series in terms of material covered and difficulty level. List of books #''Introduction to Axiomatic Set Theory'', Gaisi Takeuti, Wilson M. Zaring (1982, 2nd ed., ) #''Measure and Category – A Survey of the Analogies between Topological and Measure Spaces'', John C. Oxtoby (1980, 2nd ed., ) #''Topological Vector Spaces'', H. H. Schaefer, M. P. Wolff (1999, 2nd ed., ) #''A Course in Homological Algebra'', Peter Hilton, Urs Stamm ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Springer-Verlag
Springer Science+Business Media, commonly known as Springer, is a German multinational publishing company of books, e-books and peer-reviewed journals in science, humanities, technical and medical (STM) publishing. Originally founded in 1842 in Berlin, it expanded internationally in the 1960s, and through mergers in the 1990s and a sale to venture capitalists it fused with Wolters Kluwer and eventually became part of Springer Nature in 2015. Springer has major offices in Berlin, Heidelberg, Dordrecht, and New York City. History Julius Springer founded Springer-Verlag in Berlin in 1842 and his son Ferdinand Springer grew it from a small firm of 4 employees into Germany's then second largest academic publisher with 65 staff in 1872.Chronology ". Springer Science+Business Media. In 1964, Springer expanded its business internationall ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fractional Schrödinger Equation
A fraction is one or more equal parts of something. Fraction may also refer to: * Fraction (chemistry), a quantity of a substance collected by fractionation * Fraction (floating point number), an (ambiguous) term sometimes used to specify a part of a floating point number * Fraction (politics), a subgroup within a parliamentary party * Fraction (radiation therapy), one unit of treatment of the total radiation dose of radiation therapy that is split into multiple treatment sessions * Fraction (religion), the ceremonial act of breaking the bread during Christian Communion People with the surname * Matt Fraction, a comic book author See also * Algebraic fraction, an indicated division in which the divisor, or both dividend and divisor, are algebraic expressions ** Irrational fraction, a type of algebraic fraction * Faction (other) * '' Frazione'', a type of administrative division of an Italian ''commune'' * Free and Independent Fraction The Free and Independent Fact ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sobolev Space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of ''Lp''-norms of the function together with its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, i.e. a Banach space. Intuitively, a Sobolev space is a space of functions possessing sufficiently many derivatives for some application domain, such as partial differential equations, and equipped with a norm that measures both the size and regularity of a function. Sobolev spaces are named after the Russian mathematician Sergei Sobolev. Their importance comes from the fact that weak solutions of some important partial differential equations exist in appropriate Sobolev spaces, even when there are no strong solutions in spaces of continuous functions with the derivatives understood in the classical sense. Motivation In this section and throughout the article \Omega is an open subset of \R^n. There are ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bessel Function
Bessel functions, first defined by the mathematician Daniel Bernoulli and then generalized by Friedrich Bessel, are canonical solutions of Bessel's differential equation x^2 \frac + x \frac + \left(x^2 - \alpha^2 \right)y = 0 for an arbitrary complex number \alpha, the ''order'' of the Bessel function. Although \alpha and -\alpha produce the same differential equation, it is conventional to define different Bessel functions for these two values in such a way that the Bessel functions are mostly smooth functions of \alpha. The most important cases are when \alpha is an integer or half-integer. Bessel functions for integer \alpha are also known as cylinder functions or the cylindrical harmonics because they appear in the solution to Laplace's equation in cylindrical coordinates. #Spherical Bessel functions, Spherical Bessel functions with half-integer \alpha are obtained when the Helmholtz equation is solved in spherical coordinates. Applications of Bessel functions The Bessel f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Potential Theory
In mathematics and mathematical physics, potential theory is the study of harmonic functions. The term "potential theory" was coined in 19th-century physics when it was realized that two fundamental forces of nature known at the time, namely gravity and the electrostatic force, could be modeled using functions called the gravitational potential and electrostatic potential, both of which satisfy Poisson's equation—or in the vacuum, Laplace's equation. There is considerable overlap between potential theory and the theory of Poisson's equation to the extent that it is impossible to draw a distinction between these two fields. The difference is more one of emphasis than subject matter and rests on the following distinction: potential theory focuses on the properties of the functions as opposed to the properties of the equation. For example, a result about the singularities of harmonic functions would be said to belong to potential theory whilst a result on how the solution dep ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gamma Function
In mathematics, the gamma function (represented by , the capital letter gamma from the Greek alphabet) is one commonly used extension of the factorial function to complex numbers. The gamma function is defined for all complex numbers except the non-positive integers. For every positive integer , \Gamma(n) = (n-1)!\,. Derived by Daniel Bernoulli, for complex numbers with a positive real part, the gamma function is defined via a convergent improper integral: \Gamma(z) = \int_0^\infty t^ e^\,dt, \ \qquad \Re(z) > 0\,. The gamma function then is defined as the analytic continuation of this integral function to a meromorphic function that is holomorphic in the whole complex plane except zero and the negative integers, where the function has simple poles. The gamma function has no zeroes, so the reciprocal gamma function is an entire function. In fact, the gamma function corresponds to the Mellin transform of the negative exponential function: \Gamma(z) = \mathcal M ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |