|
Bernoulli's Inequality
In mathematics, Bernoulli's inequality (named after Jacob Bernoulli) is an inequality that approximates exponentiations of 1 + ''x''. It is often employed in real analysis. It has several useful variants: * (1 + x)^r \geq 1 + rx for every integer ''r'' ≥ 0 and real number ''x'' > −1. The inequality is strict if ''x'' ≠ 0 and ''r'' ≥ 2. * (1 + x)^r \geq 1 + rx for every even integer ''r'' ≥ 0 and every real number ''x''. * (1 + x)^r \geq 1 + rx for every integer ''r'' ≥ 0 and every real number ''x'' ≥ −2.Excluding the case and , or assuming that . * (1 + x)^r \geq 1 + rx for every real number ''r'' ≥ 1 and ''x'' ≥ −1. The inequalities are strict if ''x'' ≠ 0 and ''r'' ≠ 0, 1. * (1 + x)^r \leq 1 + rx for every real number 0 ≤ ''r'' ≤ 1 and ''x'' ≥ −1. History Jacob Bernoulli fir ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bernoulli Inequality
In mathematics, Bernoulli's inequality (named after Jacob Bernoulli) is an inequality that approximates exponentiations of 1 + ''x''. It is often employed in real analysis. It has several useful variants: * (1 + x)^r \geq 1 + rx for every integer ''r'' ≥ 0 and real number ''x'' > −1. The inequality is strict if ''x'' ≠ 0 and ''r'' ≥ 2. * (1 + x)^r \geq 1 + rx for every even integer ''r'' ≥ 0 and every real number ''x''. * (1 + x)^r \geq 1 + rx for every integer ''r'' ≥ 0 and every real number ''x'' ≥ −2.Excluding the case and , or assuming that . * (1 + x)^r \geq 1 + rx for every real number ''r'' ≥ 1 and ''x'' ≥ −1. The inequalities are strict if ''x'' ≠ 0 and ''r'' ≠ 0, 1. * (1 + x)^r \leq 1 + rx for every real number 0 ≤ ''r'' ≤ 1 and ''x'' ≥ −1. History Jacob Bernoulli first ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Induction
Mathematical induction is a method for proving that a statement ''P''(''n'') is true for every natural number ''n'', that is, that the infinitely many cases ''P''(0), ''P''(1), ''P''(2), ''P''(3), ... all hold. Informal metaphors help to explain this technique, such as falling dominoes or climbing a ladder: A proof by induction consists of two cases. The first, the base case, proves the statement for ''n'' = 0 without assuming any knowledge of other cases. The second case, the induction step, proves that ''if'' the statement holds for any given case ''n'' = ''k'', ''then'' it must also hold for the next case ''n'' = ''k'' + 1. These two steps establish that the statement holds for every natural number ''n''. The base case does not necessarily begin with ''n'' = 0, but often with ''n'' = 1, and possibly with any fixed natural number ''n'' = ''N'', establishing the truth of the statement for all natu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Binomial Theorem
In elementary algebra, the binomial theorem (or binomial expansion) describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the polynomial into a sum involving terms of the form , where the exponents and are nonnegative integers with , and the coefficient of each term is a specific positive integer depending on and . For example, for , (x+y)^4 = x^4 + 4 x^3y + 6 x^2 y^2 + 4 x y^3 + y^4. The coefficient in the term of is known as the binomial coefficient \tbinom or \tbinom (the two have the same value). These coefficients for varying and can be arranged to form Pascal's triangle. These numbers also occur in combinatorics, where \tbinom gives the number of different combinations of elements that can be chosen from an -element set. Therefore \tbinom is often pronounced as " choose ". History Special cases of the binomial theorem were known since at least the 4th century BC when Greek mathematician Euclid mentione ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sides Of An Equation
In mathematics, LHS is informal shorthand for the left-hand side of an equation. Similarly, RHS is the right-hand side. The two sides have the same value, expressed differently, since equality is symmetric. definition and example of abbreviation More generally, these terms may apply to an inequation or inequality; the right-hand side is everything on the right side of a [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
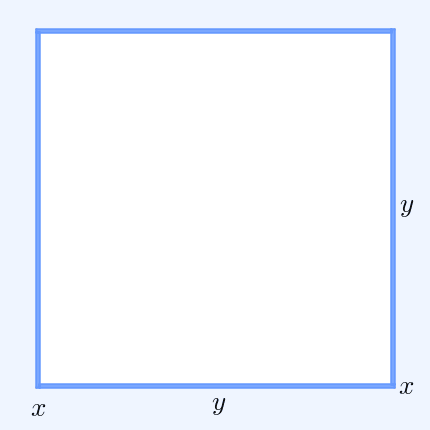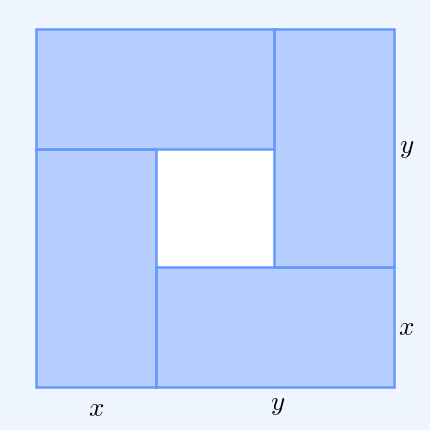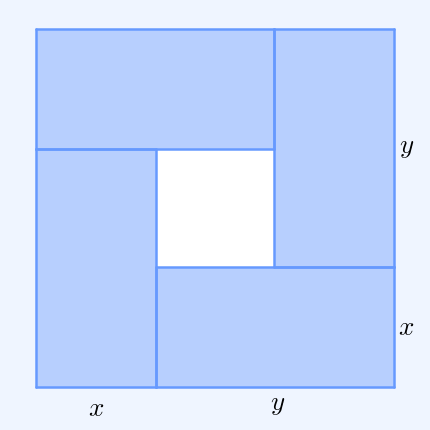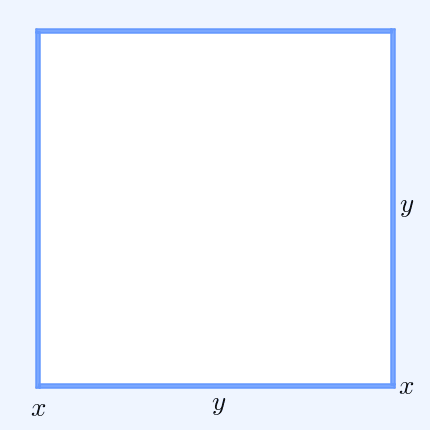
Inequality Of Arithmetic And Geometric Means
In mathematics, the inequality of arithmetic and geometric means, or more briefly the AM–GM inequality, states that the arithmetic mean of a list of non-negative real numbers is greater than or equal to the geometric mean of the same list; and further, that the two means are equal if and only if every number in the list is the same (in which case they are both that number). The simplest non-trivial case – i.e., with more than one variable – for two non-negative numbers and , is the statement that :\frac2 \ge \sqrt with equality if and only if . This case can be seen from the fact that the square of a real number is always non-negative (greater than or equal to zero) and from the elementary case of the binomial formula: :\begin 0 & \le (x-y)^2 \\ & = x^2-2xy+y^2 \\ & = x^2+2xy+y^2 - 4xy \\ & = (x+y)^2 - 4xy. \end Hence , with equality precisely when , i.e. . The AM–GM inequality then follows from taking the positive square root of both sides and then dividing both ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometric Series
In mathematics, a geometric series is the sum of an infinite number of terms that have a constant ratio between successive terms. For example, the series :\frac \,+\, \frac \,+\, \frac \,+\, \frac \,+\, \cdots is geometric, because each successive term can be obtained by multiplying the previous term by 1/2. In general, a geometric series is written as a + ar + ar^2 + ar^3 + ..., where a is the coefficient of each term and r is the common ratio between adjacent terms. The geometric series had an important role in the early development of calculus, is used throughout mathematics, and can serve as an introduction to frequently used mathematical tools such as the Taylor series, the complex Fourier series, and the matrix exponential. The name geometric series indicates each term is the geometric mean of its two neighboring terms, similar to how the name arithmetic series indicates each term is the arithmetic mean of its two neighboring terms. The sequence of geometric series ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
E (number)
The number , also known as Euler's number, is a mathematical constant approximately equal to 2.71828 that can be characterized in many ways. It is the base of a logarithm, base of the natural logarithms. It is the Limit of a sequence, limit of as approaches infinity, an expression that arises in the study of compound interest. It can also be calculated as the sum of the infinite Series (mathematics), series e = \sum\limits_^ \frac = 1 + \frac + \frac + \frac + \cdots. It is also the unique positive number such that the graph of the function has a slope of 1 at . The (natural) exponential function is the unique function that equals its own derivative and satisfies the equation ; hence one can also define as . The natural logarithm, or logarithm to base , is the inverse function to the natural exponential function. The natural logarithm of a number can be defined directly as the integral, area under the curve between and , in which case is the value of for which ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Derivative
In mathematics, the derivative of a function of a real variable measures the sensitivity to change of the function value (output value) with respect to a change in its argument (input value). Derivatives are a fundamental tool of calculus. For example, the derivative of the position of a moving object with respect to time is the object's velocity: this measures how quickly the position of the object changes when time advances. The derivative of a function of a single variable at a chosen input value, when it exists, is the slope of the tangent line to the graph of the function at that point. The tangent line is the best linear approximation of the function near that input value. For this reason, the derivative is often described as the "instantaneous rate of change", the ratio of the instantaneous change in the dependent variable to that of the independent variable. Derivatives can be generalized to functions of several real variables. In this generalization, the deriv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zero To The Power Of Zero
Zero to the power of zero, denoted by , is a mathematical expression that is either defined as 1 or left undefined, depending on context. In algebra and combinatorics, one typically defines . In mathematical analysis, the expression is sometimes left undefined. Computer programming languages and software also have differing ways of handling this expression. Discrete exponents Many widely used formulas involving natural-number exponents require to be defined as . For example, the following three interpretations of make just as much sense for as they do for positive integers : * The interpretation of as an empty product assigns it the value . * The combinatorial interpretation of is the number of 0-tuples of elements from a -element set; there is exactly one 0-tuple. * The set-theoretic interpretation of is the number of functions from the empty set to a -element set; there is exactly one such function, namely, the empty function. All three of these specialize ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting poin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parity (mathematics)
In mathematics, parity is the property of an integer of whether it is even or odd. An integer is even if it is a multiple of two, and odd if it is not.. For example, −4, 0, 82 are even because \begin -2 \cdot 2 &= -4 \\ 0 \cdot 2 &= 0 \\ 41 \cdot 2 &= 82 \end By contrast, −3, 5, 7, 21 are odd numbers. The above definition of parity applies only to integer numbers, hence it cannot be applied to numbers like 1/2 or 4.201. See the section "Higher mathematics" below for some extensions of the notion of parity to a larger class of "numbers" or in other more general settings. Even and odd numbers have opposite parities, e.g., 22 (even number) and 13 (odd number) have opposite parities. In particular, the parity of zero is even. Any two consecutive integers have opposite parity. A number (i.e., integer) expressed in the decimal numeral system is even or odd according to whether its last digit is even or odd. That is, if the last digit is 1, 3, 5, 7, or 9, then it is odd; other ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Real Number
In mathematics, a real number is a number that can be used to measurement, measure a ''continuous'' one-dimensional quantity such as a distance, time, duration or temperature. Here, ''continuous'' means that values can have arbitrarily small variations. Every real number can be almost uniquely represented by an infinite decimal expansion. The real numbers are fundamental in calculus (and more generally in all mathematics), in particular by their role in the classical definitions of limit (mathematics), limits, continuous function, continuity and derivatives. The set of real numbers is mathematical notation, denoted or \mathbb and is sometimes called "the reals". The adjective ''real'' in this context was introduced in the 17th century by René Descartes to distinguish real numbers, associated with physical reality, from imaginary numbers (such as the square roots of ), which seemed like a theoretical contrivance unrelated to physical reality. The real numbers subset, include t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |