|
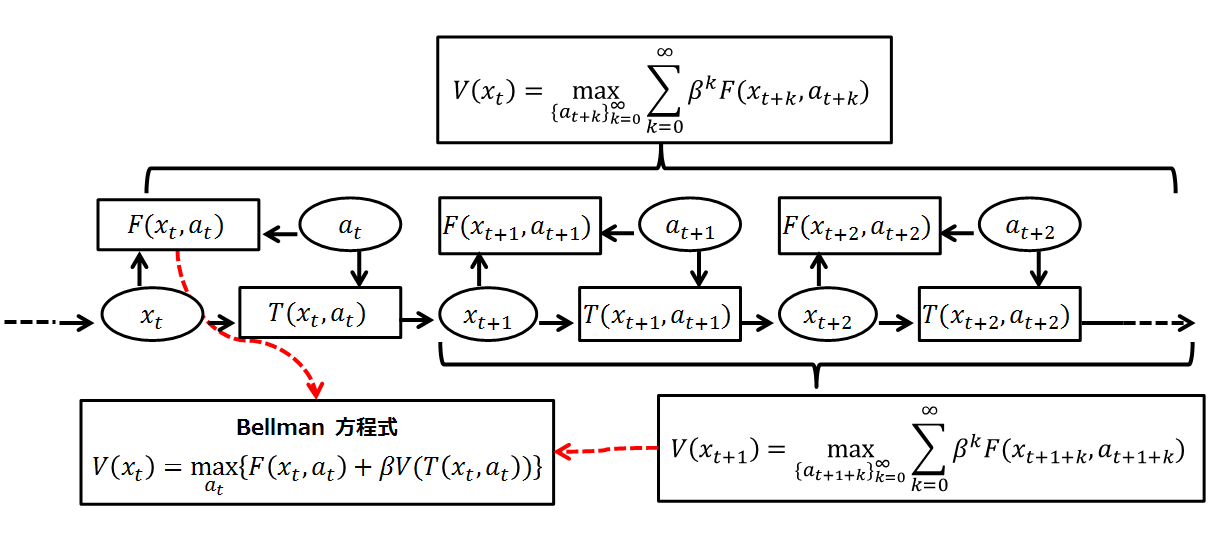
Bellman Equation
A Bellman equation, named after Richard E. Bellman, is a necessary condition for optimality associated with the mathematical Optimization (mathematics), optimization method known as dynamic programming. It writes the "value" of a decision problem at a certain point in time in terms of the payoff from some initial choices and the "value" of the remaining decision problem that results from those initial choices. This breaks a dynamic optimization problem into a sequence of simpler subproblems, as Bellman's “principle of optimality" prescribes. The equation applies to algebraic structures with a total ordering; for algebraic structures with a partial ordering, the generic Bellman's equation can be used. The Bellman equation was first applied to engineering control theory and to other topics in applied mathematics, and subsequently became an important tool in economic theory; though the basic concepts of dynamic programming are prefigured in John von Neumann and Oskar Morgenstern's ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bellman Flow Chart
Bellman may refer to: * Town crier, an officer of the court who makes public pronouncements * Bellhop, a hotel porter * Bellman (surname) * Bellman (diving), a standby diver and diver's attendant * Bellman hangar, a prefabricated, portable aircraft hangar * Bellman's Head, a headland point in Stonehaven Bay, Scotland Arts * The Bellman (film), ''The Bellman'' (film), a 1945 French drama film * The Bellman (literary magazine), ''The Bellman'' (literary magazine), a 1906–1919 American periodical * The Bellman (character), a character in the ''Thursday Next'' novels * "Bellman", a character in Lewis Carroll's poem ''The Hunting of the Snark'' * Bellman Prize, a literature prize awarded by the Swedish Academy * Bellman joke, a type of Swedish joke * Zvončari, a Croatian folk custom Sciences *Bellman equation, a condition for optimality in dynamic programming *Hamilton–Jacobi–Bellman equation, a condition for optimality of a control with respect to a loss function *Bellman– ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
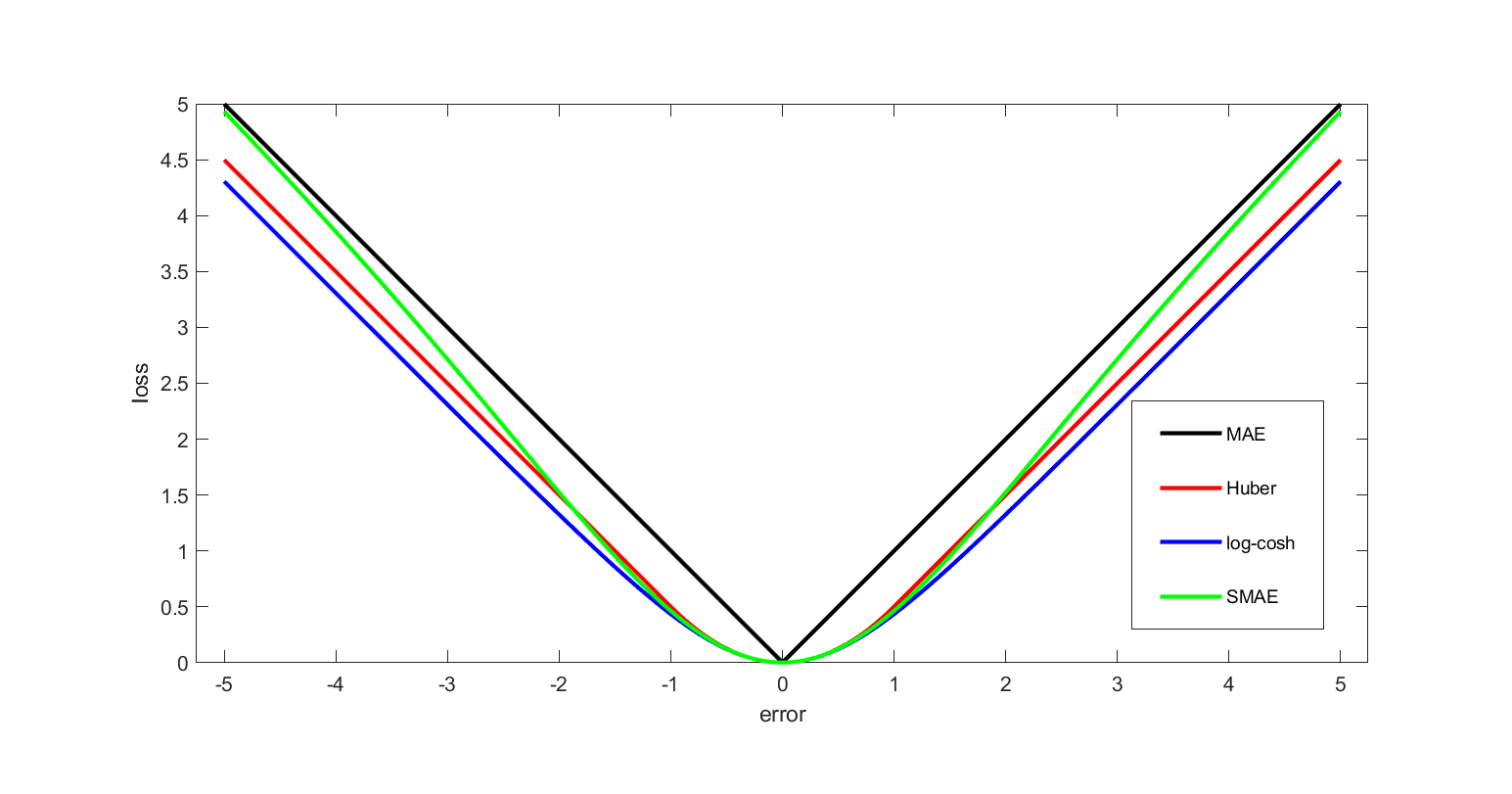
Loss Function
In mathematical optimization and decision theory, a loss function or cost function (sometimes also called an error function) is a function that maps an event or values of one or more variables onto a real number intuitively representing some "cost" associated with the event. An optimization problem seeks to minimize a loss function. An objective function is either a loss function or its opposite (in specific domains, variously called a reward function, a profit function, a utility function, a fitness function, etc.), in which case it is to be maximized. The loss function could include terms from several levels of the hierarchy. In statistics, typically a loss function is used for parameter estimation, and the event in question is some function of the difference between estimated and true values for an instance of data. The concept, as old as Pierre-Simon Laplace, Laplace, was reintroduced in statistics by Abraham Wald in the middle of the 20th century. In the context of economi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Optimal Control
Optimal control theory is a branch of control theory that deals with finding a control for a dynamical system over a period of time such that an objective function is optimized. It has numerous applications in science, engineering and operations research. For example, the dynamical system might be a spacecraft with controls corresponding to rocket thrusters, and the objective might be to reach the Moon with minimum fuel expenditure. Or the dynamical system could be a nation's economy, with the objective to minimize unemployment; the controls in this case could be fiscal and monetary policy. A dynamical system may also be introduced to embed operations research problems within the framework of optimal control theory. Optimal control is an extension of the calculus of variations, and is a mathematical optimization method for deriving control policies. The method is largely due to the work of Lev Pontryagin and Richard Bellman in the 1950s, after contributions to calculus of v ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Functional Equation
In mathematics, a functional equation is, in the broadest meaning, an equation in which one or several functions appear as unknowns. So, differential equations and integral equations are functional equations. However, a more restricted meaning is often used, where a ''functional equation'' is an equation that relates several values of the same function. For example, the logarithm functions are essentially characterized by the ''logarithmic functional equation'' \log(xy)=\log(x) + \log(y). If the domain of the unknown function is supposed to be the natural numbers, the function is generally viewed as a sequence, and, in this case, a functional equation (in the narrower meaning) is called a recurrence relation. Thus the term ''functional equation'' is used mainly for real functions and complex functions. Moreover a smoothness condition is often assumed for the solutions, since without such a condition, most functional equations have very irregular solutions. For example, the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Recursion
Recursion occurs when the definition of a concept or process depends on a simpler or previous version of itself. Recursion is used in a variety of disciplines ranging from linguistics to logic. The most common application of recursion is in mathematics and computer science, where a function (mathematics), function being defined is applied within its own definition. While this apparently defines an infinite number of instances (function values), it is often done in such a way that no infinite loop or infinite chain of references can occur. A process that exhibits recursion is ''recursive''. Video feedback displays recursive images, as does an infinity mirror. Formal definitions In mathematics and computer science, a class of objects or methods exhibits recursive behavior when it can be defined by two properties: * A simple ''base case'' (or cases) — a terminating scenario that does not use recursion to produce an answer * A ''recursive step'' — a set of rules that reduce ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
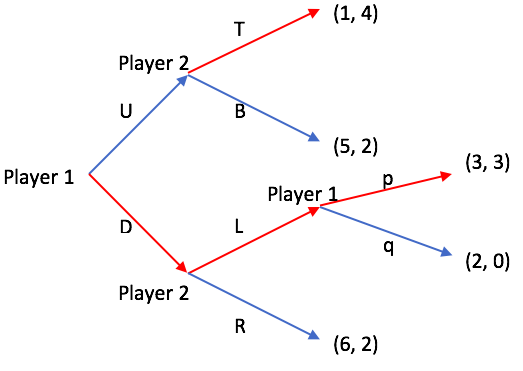
Subgame Perfect Equilibrium
In game theory, a subgame perfect equilibrium (SPE), or subgame perfect Nash equilibrium (SPNE), is a refinement of the Nash equilibrium concept, specifically designed for dynamic games where players make sequential decisions. A strategy profile is an SPE if it represents a Nash equilibrium in every possible subgame of the original game. Informally, this means that at any point in the game, the players' behavior from that point onward should represent a Nash equilibrium of the continuation game (i.e. of the subgame), no matter what happened before. This ensures that strategies are credible and rational throughout the entire game, eliminating non-credible threats. Every finite extensive game with complete information (all players know the complete state of the game) and perfect recall (each player remembers all their previous actions and knowledge throughout the game) has a subgame perfect equilibrium. A common method for finding SPE in finite games is backward induction, wher ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Game Theory
Game theory is the study of mathematical models of strategic interactions. It has applications in many fields of social science, and is used extensively in economics, logic, systems science and computer science. Initially, game theory addressed two-person zero-sum games, in which a participant's gains or losses are exactly balanced by the losses and gains of the other participant. In the 1950s, it was extended to the study of non zero-sum games, and was eventually applied to a wide range of Human behavior, behavioral relations. It is now an umbrella term for the science of rational Decision-making, decision making in humans, animals, and computers. Modern game theory began with the idea of mixed-strategy equilibria in two-person zero-sum games and its proof by John von Neumann. Von Neumann's original proof used the Brouwer fixed-point theorem on continuous mappings into compact convex sets, which became a standard method in game theory and mathematical economics. His paper was f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Optimal Substructure
In computer science, a problem is said to have optimal substructure if an optimal solution can be constructed from optimal solutions of its subproblems. This property is used to determine the usefulness of greedy algorithms for a problem.{{cite book, title=Introduction to Algorithms , edition=3rd, last1=Cormen, first1=Thomas H. , last2=Leiserson , first2=Charles E. , last3=Rivest, first3=Ronald L. , last4= Stein , first4=Clifford, date=2009 , isbn=978-0-262-03384-8, publisher=MIT Press, authorlink1=Thomas H. Cormen , authorlink2=Charles E. Leiserson, authorlink3=Ron Rivest , authorlink4=Clifford Stein Typically, a greedy algorithm is used to solve a problem with optimal substructure if it can be proven by induction that this is optimal at each step. Otherwise, provided the problem exhibits overlapping subproblems as well, divide-and-conquer methods or dynamic programming may be used. If there are no appropriate greedy algorithms and the problem fails to exhibit overlapping sub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
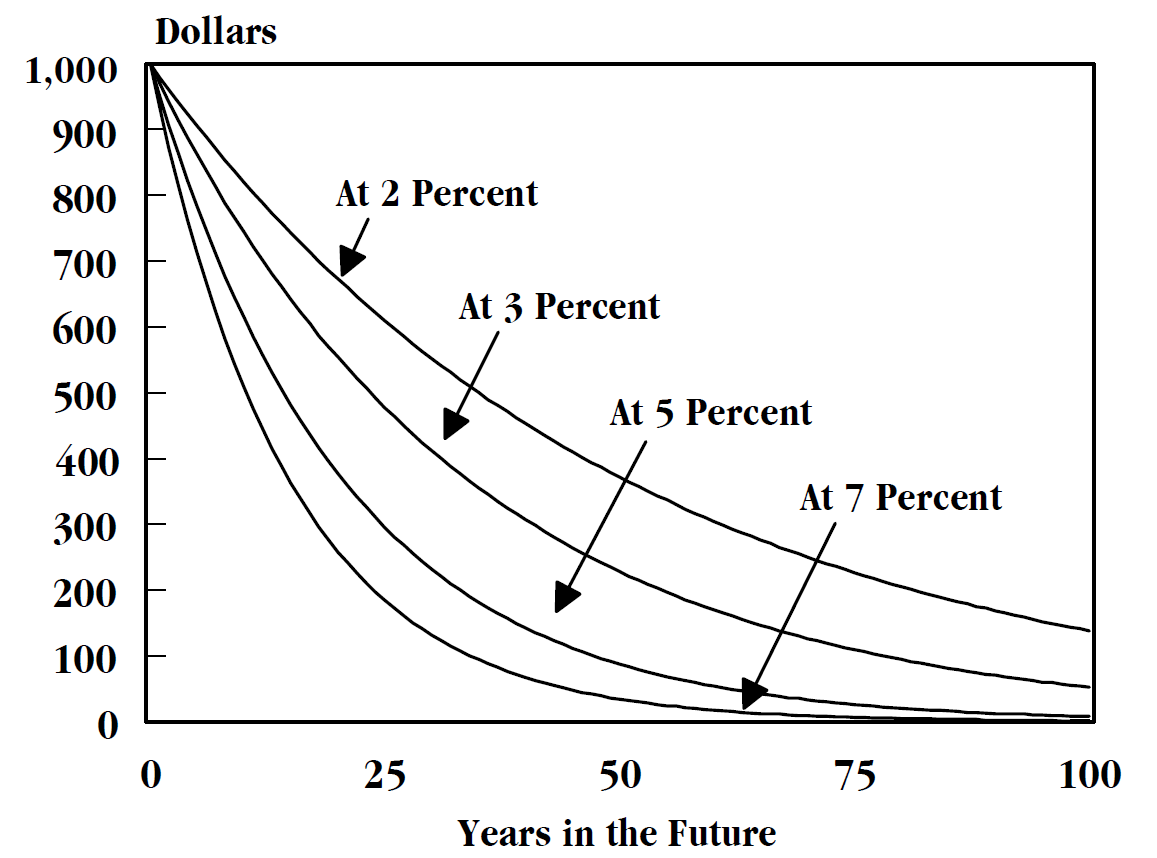
Discount Factor
In finance, discounting is a mechanism in which a debtor obtains the right to delay payments to a creditor, for a defined period of time, in exchange for a charge or fee.See "Time Value", "Discount", "Discount Yield", "Compound Interest", "Efficient Market", "Market Value" and "Opportunity Cost" in Downes, J. and Goodman, J. E. ''Dictionary of Finance and Investment Terms'', Baron's Financial Guides, 2003. Essentially, the party that owes money in the present purchases the right to delay the payment until some future date.See "Discount", "Compound Interest", "Efficient Markets Hypothesis", "Efficient Resource Allocation", "Pareto-Optimality", "Price", "Price Mechanism" and "Efficient Market" in Black, John, ''Oxford Dictionary of Economics'', Oxford University Press, 2002. This transaction is based on the fact that most people prefer current interest to delayed interest because of mortality effects, impatience effects, and salience effects. The discount, or charge, is the dif ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Backward Induction
Backward induction is the process of determining a sequence of optimal choices by reasoning from the endpoint of a problem or situation back to its beginning using individual events or actions. Backward induction involves examining the final point in a series of decisions and identifying the optimal process or action required to arrive at that point. This process continues backward until the best action for every possible point along the sequence is determined. Backward induction was first utilized in 1875 by Arthur Cayley, who discovered the method while attempting to solve the secretary problem. In dynamic programming, a method of mathematical optimization, backward induction is used for solving the Bellman equation. In the related fields of automated planning and scheduling and automated theorem proving, the method is called backward search or backward chaining. In chess, it is called retrograde analysis. In game theory, a variant of backward induction is used to compute subgame ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Recursion
Recursion occurs when the definition of a concept or process depends on a simpler or previous version of itself. Recursion is used in a variety of disciplines ranging from linguistics to logic. The most common application of recursion is in mathematics and computer science, where a function (mathematics), function being defined is applied within its own definition. While this apparently defines an infinite number of instances (function values), it is often done in such a way that no infinite loop or infinite chain of references can occur. A process that exhibits recursion is ''recursive''. Video feedback displays recursive images, as does an infinity mirror. Formal definitions In mathematics and computer science, a class of objects or methods exhibits recursive behavior when it can be defined by two properties: * A simple ''base case'' (or cases) — a terminating scenario that does not use recursion to produce an answer * A ''recursive step'' — a set of rules that reduce ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discrete Time
In mathematical dynamics, discrete time and continuous time are two alternative frameworks within which variables that evolve over time are modeled. Discrete time Discrete time views values of variables as occurring at distinct, separate "points in time", or equivalently as being unchanged throughout each non-zero region of time ("time period")—that is, time is viewed as a discrete variable. Thus a non-time variable jumps from one value to another as time moves from one time period to the next. This view of time corresponds to a digital clock that gives a fixed reading of 10:37 for a while, and then jumps to a new fixed reading of 10:38, etc. In this framework, each variable of interest is measured once at each time period. The number of measurements between any two time periods is finite. Measurements are typically made at sequential integer values of the variable "time". A discrete signal or discrete-time signal is a time series consisting of a sequence of quantities. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |