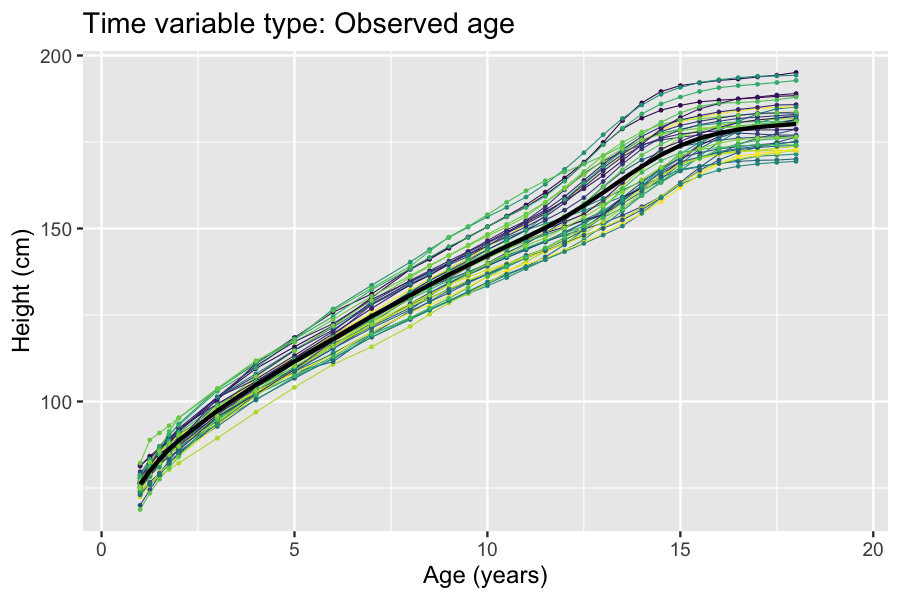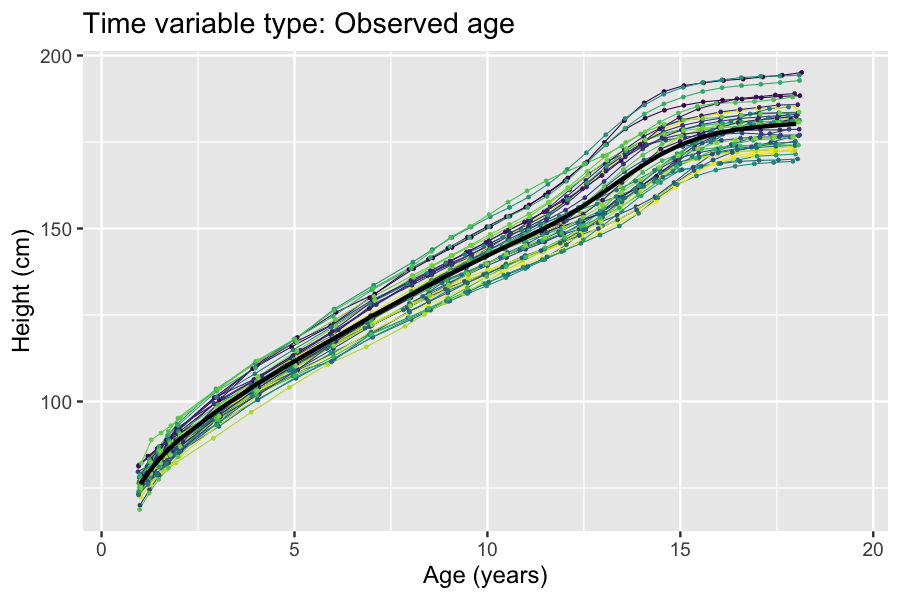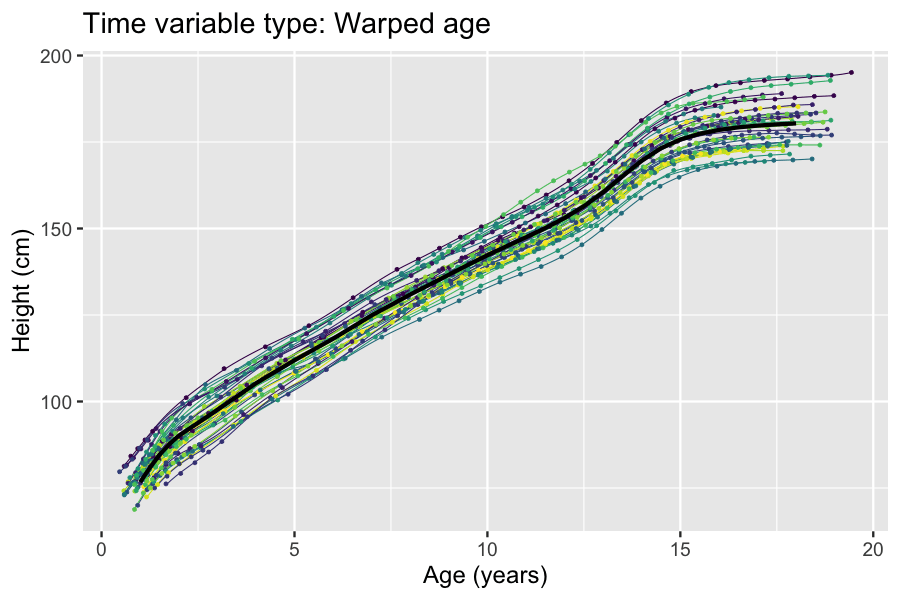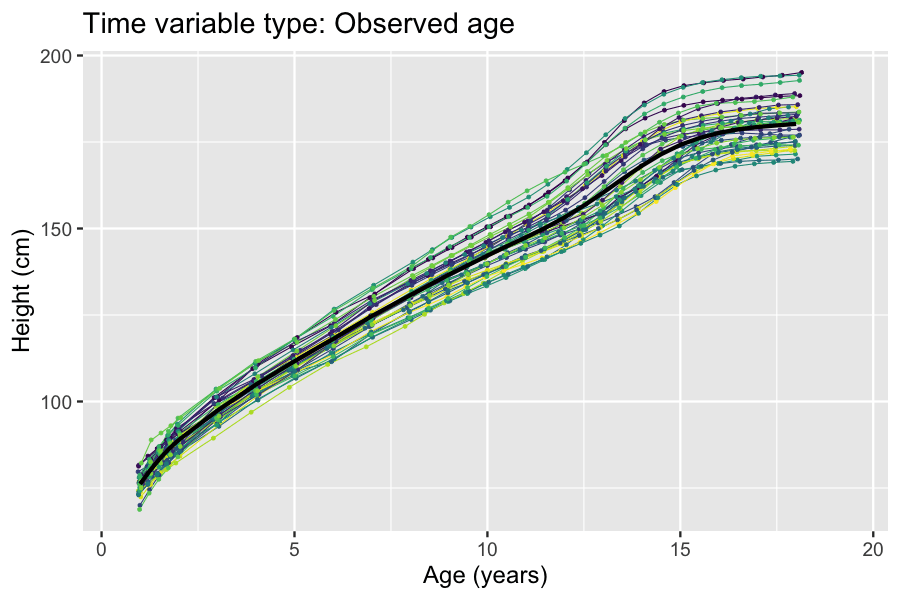
|
Behavioral Modeling
The behavioral approach to systems theory and control theory was initiated in the late-1970s by J. C. Willems as a result of resolving inconsistencies present in classical approaches based on state-space, transfer function, and convolution representations. This approach is also motivated by the aim of obtaining a general framework for system analysis and control that respects the underlying physics. The main object in the behavioral setting is the behavior – the set of all signals compatible with the system. An important feature of the behavioral approach is that it does not distinguish a priority between input and output variables. Apart from putting system theory and control on a rigorous basis, the behavioral approach unified the existing approaches and brought new results on controllability for nD systems, control via interconnection,J.C. Willems On interconnections, control, and feedback IEEE Transactions on Automatic Control Volume 42, pages 326-339, 1997 Available online ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Systems Theory
Systems theory is the interdisciplinary study of systems, i.e. cohesive groups of interrelated, interdependent components that can be natural or human-made. Every system has causal boundaries, is influenced by its context, defined by its structure, function and role, and expressed through its relations with other systems. A system is "more than the sum of its parts" by expressing synergy or emergent behavior. Changing one component of a system may affect other components or the whole system. It may be possible to predict these changes in patterns of behavior. For systems that learn and adapt, the growth and the degree of adaptation depend upon how well the system is engaged with its environment and other contexts influencing its organization. Some systems support other systems, maintaining the other system to prevent failure. The goals of systems theory are to model a system's dynamics, constraints, conditions, and relations; and to elucidate principles (such as purpose, meas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Control Theory
Control theory is a field of mathematics that deals with the control of dynamical systems in engineered processes and machines. The objective is to develop a model or algorithm governing the application of system inputs to drive the system to a desired state, while minimizing any ''delay'', ''overshoot'', or ''steady-state error'' and ensuring a level of control stability; often with the aim to achieve a degree of optimality. To do this, a controller with the requisite corrective behavior is required. This controller monitors the controlled process variable (PV), and compares it with the reference or set point (SP). The difference between actual and desired value of the process variable, called the ''error'' signal, or SP-PV error, is applied as feedback to generate a control action to bring the controlled process variable to the same value as the set point. Other aspects which are also studied are controllability and observability. Control theory is used in control sys ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jan Camiel Willems
Jan Camiel Willems (18 September 1939 – 31 August 2013) was a Belgian mathematical system theorist who has done most of his scientific work while residing in the Netherlands and the United States. He is most noted for the introduction of the notion of a dissipative system and for the development of the behavioral approach to systems theory. Biography Jan Willems was born in Bruges in 1939. He studied engineering at the University of Ghent, obtained the M.Sc. degree from the University of Rhode Island, and the Ph.D. degree from the Massachusetts Institute of Technology in electrical engineering in 1968. He was an assistant professor in the Department of Electrical Engineering at MIT from 1968 to 1973. On 1 February 1973 he was appointed Professor of Systems and Control in the Mathematics Department of the University of Groningen. In 2003 he became emeritus professor. Afterwards, he became Guest Professor at the KU Leuven. He served terms as chairperson of the European Union Contr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Physics
Physics is the natural science that studies matter, its fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which relates to the order of nature, or, in other words, to the regular succession of events." Physics is one of the most fundamental scientific disciplines, with its main goal being to understand how the universe behaves. "Physics is one of the most fundamental of the sciences. Scientists of all disciplines use the ideas of physics, including chemists who study the structure of molecules, paleontologists who try to reconstruct how dinosaurs walked, and climatologists who study how human activities affect the atmosphere and oceans. Physics is also the foundation of all engineering and technology. No engineer could design a flat-screen TV, an interplanetary spacecraft, or even a better mousetrap without first understanding the basic laws of physics ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Controllability
Controllability is an important property of a control system, and the controllability property plays a crucial role in many control problems, such as stabilization of unstable systems by feedback, or optimal control. Controllability and observability are dual aspects of the same problem. Roughly, the concept of controllability denotes the ability to move a system around in its entire configuration space using only certain admissible manipulations. The exact definition varies slightly within the framework or the type of models applied. The following are examples of variations of controllability notions which have been introduced in the systems and control literature: * State controllability * Output controllability * Controllability in the behavioural framework State controllability The state of a deterministic system, which is the set of values of all the system's state variables (those variables characterized by dynamic equations), completely describes the system at any give ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sabine Van Huffel
Sabine J. A. Van Huffel (born September 26, 1958) is a Belgian computer scientist, applied mathematician, and electrical engineer, whose research concerns computational methods for medical diagnostics, and in particular methods based on total least squares. Education and career Van Huffel was born in Menen. She earned bachelor's and doctoral degrees from KU Leuven in 1981 and 1987, with Joos Vandewalle as her doctoral advisor. Her dissertation, ''Analysis of the Total Least Squares Problem and its use in parameter estimation'', concerned total least squares methods for parameter estimation. She is a full professor at KU Leuven since 2002 . and a Distinguished Professor of Electrical Engineering at Eindhoven University of Technology (TU/e) since 2014 (until 2022). Book With Vandewalle, Van Huffel is the author of the book ''The Total Least Squares Problem: Computational Aspects and Analysis'' (SIAM, 1991). Recognition Van Huffel is a fellow of the IEEE and the recipient of an hon ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Superposition Principle
The superposition principle, also known as superposition property, states that, for all linear systems, the net response caused by two or more stimuli is the sum of the responses that would have been caused by each stimulus individually. So that if input ''A'' produces response ''X'' and input ''B'' produces response ''Y'' then input (''A'' + ''B'') produces response (''X'' + ''Y''). A function F(x) that satisfies the superposition principle is called a linear function. Superposition can be defined by two simpler properties: additivity F(x_1+x_2)=F(x_1)+F(x_2) \, and homogeneity F(a x)=a F(x) \, for scalar . This principle has many applications in physics and engineering because many physical systems can be modeled as linear systems. For example, a beam can be modeled as a linear system where the input stimulus is the load on the beam and the output response is the deflection of the beam. The importance of linear systems is that they are easier to analyze mathematical ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polynomial Matrix
In mathematics, a polynomial matrix or matrix of polynomials is a matrix whose elements are univariate or multivariate polynomials. Equivalently, a polynomial matrix is a polynomial whose coefficients are matrices. A univariate polynomial matrix ''P'' of degree ''p'' is defined as: :P = \sum_^p A(n)x^n = A(0)+A(1)x+A(2)x^2+ \cdots +A(p)x^p where A(i) denotes a matrix of constant coefficients, and A(p) is non-zero. An example 3×3 polynomial matrix, degree 2: : P=\begin 1 & x^2 & x \\ 0 & 2x & 2 \\ 3x+2 & x^2-1 & 0 \end =\begin 1 & 0 & 0 \\ 0 & 0 & 2 \\ 2 & -1 & 0 \end +\begin 0 & 0 & 1 \\ 0 & 2 & 0 \\ 3 & 0 & 0 \endx+\begin 0 & 1 & 0 \\ 0 & 0 & 0 \\ 0 & 1 & 0 \endx^2. We can express this by saying that for a ring ''R'', the rings M_n(R and (M_n(R)) /math> are isomorphic. Properties *A polynomial matrix over a field with determinant equal to a non-zero element of that field is called unimodular, and has an inverse that is also a polynomial matrix. Note that the only sca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Model (abstract)
A conceptual model is a representation of a system. It consists of concepts used to help people know, understand, or simulate a subject the model represents. In contrast, physical models are physical object such as a toy model that may be assembled and made to work like the object it represents. The term may refer to models that are formed after a conceptualization or generalization process. Conceptual models are often abstractions of things in the real world, whether physical or social. Semantic studies are relevant to various stages of concept formation. Semantics is basically about concepts, the meaning that thinking beings give to various elements of their experience. Overview Models of concepts and models that are conceptual The term ''conceptual model'' is normal. It could mean "a model of concept" or it could mean "a model that is conceptual." A distinction can be made between ''what models are'' and ''what models are made of''. With the exception of iconic m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Observability
Observability is a measure of how well internal states of a system can be inferred from knowledge of its external outputs. In control theory, the observability and controllability of a linear system are mathematical duals. The concept of observability was introduced by the Hungarian-American engineer Rudolf E. Kálmán for linear dynamic systems. A dynamical system designed to estimate the state of a system from measurements of the outputs is called a state observer or simply an observer for that system. Definition Consider a physical system modeled in state-space representation. A system is said to be observable if, for every possible evolution of state and control vectors, the current state can be estimated using only the information from outputs (physically, this generally corresponds to information obtained by sensors). In other words, one can determine the behavior of the entire system from the system's outputs. On the other hand, if the system is not observable, there ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Variable (mathematics)
In mathematics, a variable (from Latin '' variabilis'', "changeable") is a symbol that represents a mathematical object. A variable may represent a number, a vector, a matrix, a function, the argument of a function, a set, or an element of a set. Algebraic computations with variables as if they were explicit numbers solve a range of problems in a single computation. For example, the quadratic formula solves any quadratic equation by substituting the numeric values of the coefficients of that equation for the variables that represent them in the quadratic formula. In mathematical logic, a ''variable'' is either a symbol representing an unspecified term of the theory (a meta-variable), or a basic object of the theory that is manipulated without referring to its possible intuitive interpretation. History In ancient works such as Euclid's ''Elements'', single letters refer to geometric points and shapes. In the 7th century, Brahmagupta used different colours to represe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Latent Variable
In statistics, latent variables (from Latin: present participle of ''lateo'', “lie hidden”) are variables that can only be inferred indirectly through a mathematical model from other observable variables that can be directly observed or measured. Such '' latent variable models'' are used in many disciplines, including political science, demography, engineering, medicine, ecology, physics, machine learning/artificial intelligence, bioinformatics, chemometrics, natural language processing, management and the social sciences. Latent variables may correspond to aspects of physical reality. These could in principle be measured, but may not be for practical reasons. In this situation, the term ''hidden variables'' is commonly used (reflecting the fact that the variables are meaningful, but not observable). Other latent variables correspond to abstract concepts, like categories, behavioral or mental states, or data structures. The terms ''hypothetical variables'' or ''hypothetica ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |